下肢康复机器人是通过模拟正常人行走的步态规律,帮助由于各种原因导致的下肢偏瘫患者,进行康复训练的一种机电一体化系统。随着人口老龄化的加重,因脊髓损伤以及脑梗等疾病引起的下肢运动功能障碍的患者越来越多。因此,诸多学者开始关注研究下肢康复机器人的控制方法和控制策略。滑模控制^[1]具有快速响应且在控制过程中与控制对象的参数变化及扰动无关、不需要系统在线进行辨识等特点,因此,滑模控制成为机器人装置的首选方法。

在人机交互的过程中,下肢康复机器人滑模控制系统会存在抖振现象,机器人的跟踪效果不够精确,且对于刚性结构而言,跟踪的精度不够,很可能对患者产生二次伤害。杨婷等^[2]对比了基于估计模型和模型上界的两种滑模控制方法,发现两种方法都可以实现对目标轨迹的跟踪,但从控制输入来看,两者都存在一定程度的抖振现象。徐杰等^[3]将切换函数和趋近律一同在控制器中进行设计,达到实时补偿的效果,并在一定程度上削弱系统的抖振。张俊辉等^[4]改进了饱和函数趋近律,并对改进后的滑模可达性进行了证明,结果表明改进后的趋近律具有更好的跟踪性能。 基于此,笔者针对下肢康复机器人滑模控制系统运行过程中产生的抖振现象,设计了一种“双幂次+指数式”趋近律的滑模控制方法,为康复机器人的进一步研究提供一定的参考。

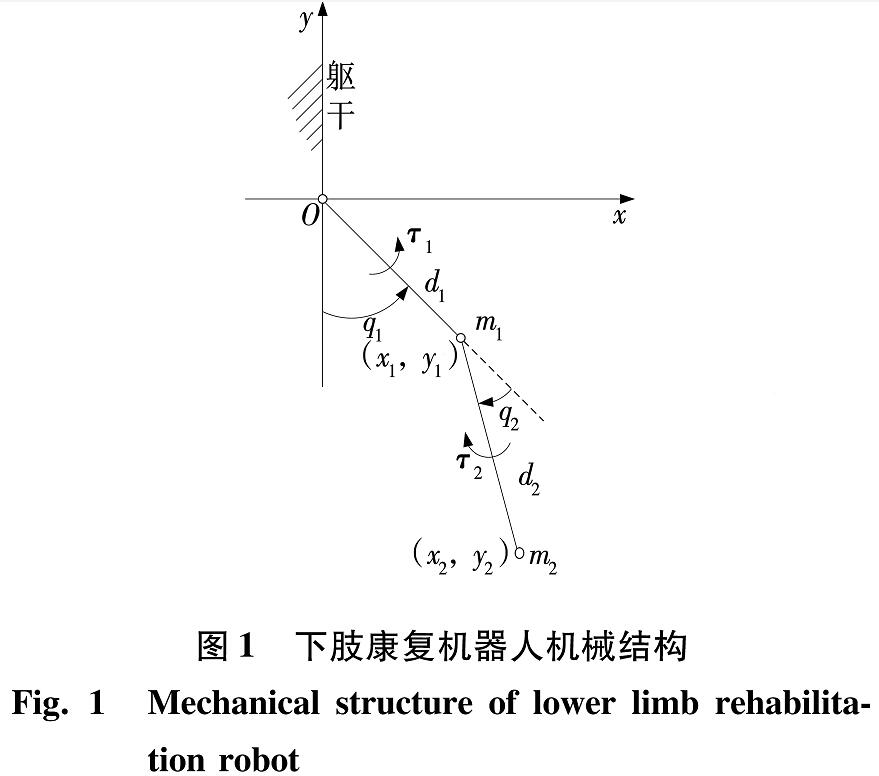
下肢康复机器人机械结构坐标图^[5]如图1所示。

图1 下肢康复机器人机械结构
Fig.1 Mechanical structure of lower limb rehabilitation robot

利用拉格朗日的方法对下肢康复机器人的关节机械装置建立动力学模型^[6-7]:

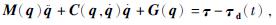
式中:M(q)——n×n阶转动惯量矩阵;

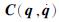——n×n阶哥氏力和向心力向量;

G(q)——n×1阶重力向量;

q——关节变量的向量,q∈Rⁿ;

τ——执行机构施加的关节控制扭矩向量,τ∈Rⁿ;

τ_d——外界干扰量。

则实际的控制对象为

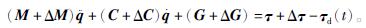
将建模误差、参数变化、机械装置之间的摩擦及其他不确定因素视为外界干扰量E,则

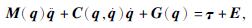
其中,

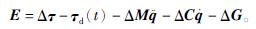
取双关节下肢康复机器人理想的位置跟踪指令为q_d(t),实际的位置跟踪指令为q(t),则双关节的跟踪误差为

e=q_d(t)-q(t),

则

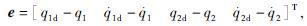
式中:q_1d、q_2d——髋关节和膝关节的理想位置;

q₁、q₂——髋关节和膝关节跟踪的实际位置;

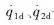——髋关节和膝关节的理想速度;

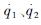——髋关节和膝关节的实际速度。

设计滑模函数^[8]为

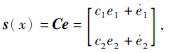
其中,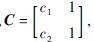

则

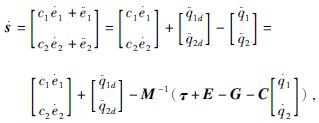
滑模控制器为

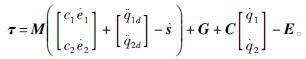(1)

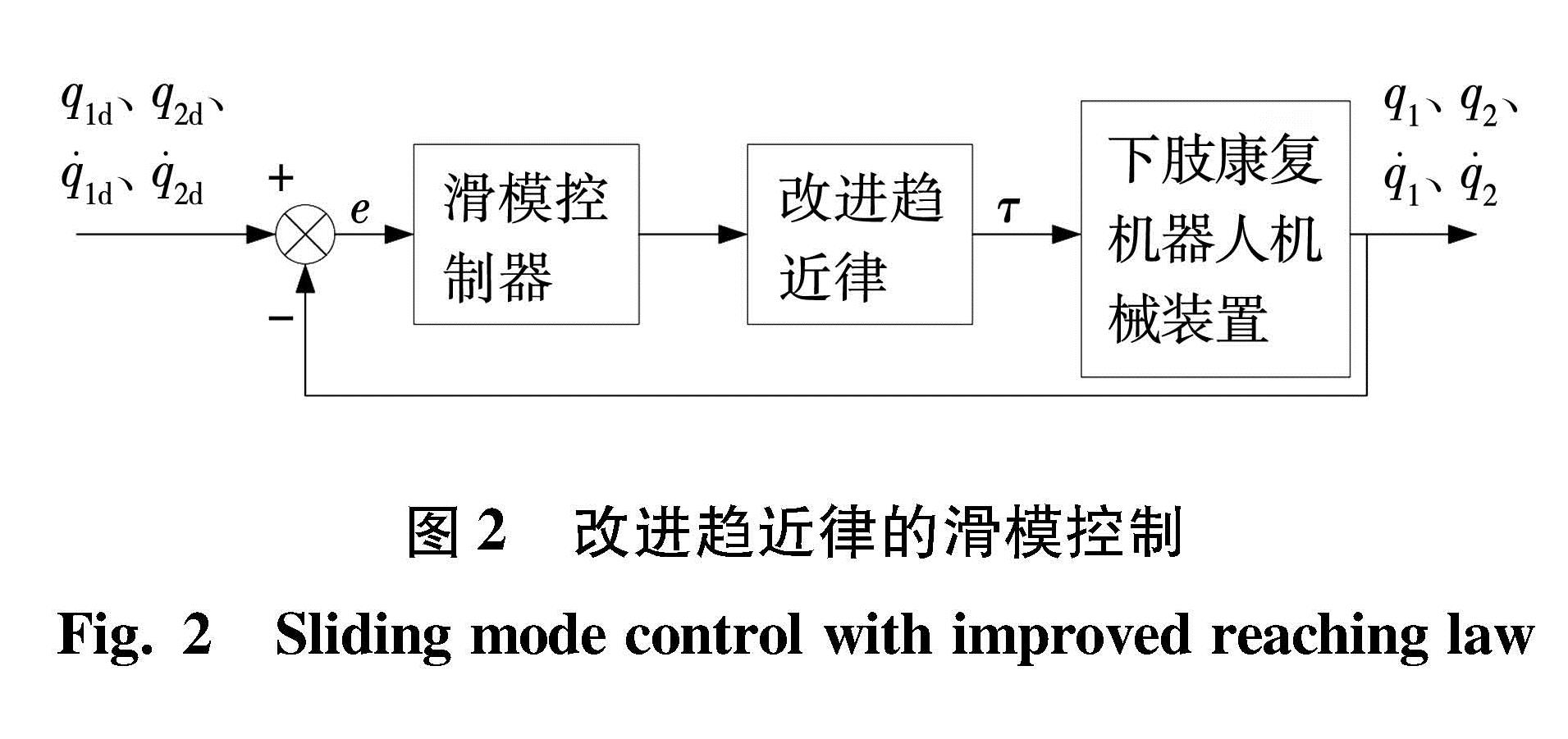
控制结构图如图2所示。

图2 改进趋近律的滑模控制
Fig.2 Sliding mode control with improved reaching law

单幂次趋近律为

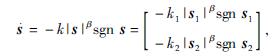(2)

其中k>0,β>1且满足滑模的到达条件ss^.<0^[9]。

将式(2)代入式(1),可得控制率

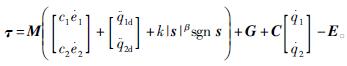(3)

在该控制率中,由于E是未知的,控制率在实际应用中无法实现,因此取E_c为E的估计值,采用E_c替代式(3)中的E,则控制率为

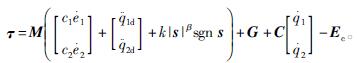(4)

将式(4)代入式(1),可得

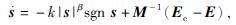(5)

取E上界为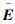,设计E_c为

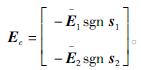
取李亚普诺夫函数为

V=1/2s^Ts,(6)

对式(6)求导,联合式(3)～(5),可得

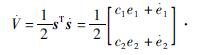
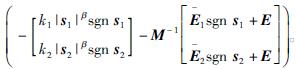
显然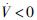,根据李亚普诺夫直接法可判定系统是稳定的^[10]。

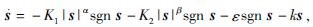,其中,K₁>0,K₂>0,0<α<1,ε>0。

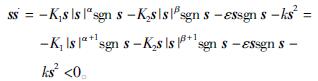
因此,改进的趋近律满足滑模可达性条件。式中|s|<1可以通过减小α的值来增大系统状态的趋近速度; |s|>1,α越小,-K₁s|s|^αsgn s相对于-K₂s|s|^βsgn s在系统中起的作用,要小得多,可忽略不计。|s|>1,可以通过增大β来增大系统状态的趋近速度; |s|<1,β越大,-K₂s|s|^βsgn s在系统中起到的作用就很小,可以忽略不计。用-εsgn s-ks来增加系统的动态品质,使得当s趋近于零时刻,趋近的速度是ε,而不是零,保证系统在有限的时间到达。以此来削弱系统的抖振,提高系统的稳定性。

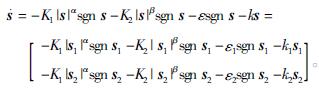(7)

将式(7)代入式(1),并将E_c替换为E系统的控制率为

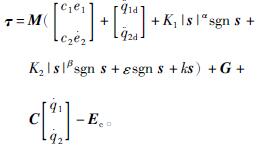(8)

将式(8)代入式(1),可得

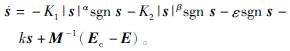(9)

对式(6)求导,并结合式(8)和(9)可得

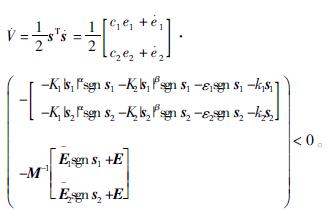
根据李亚普诺夫直接法可判定系统是稳定的。

为了使仿真实验能够更贴近于实际应用,以一男子为例对其进行动力学分析计算^[5],该男子体重为61 kg、身高为 1 667 mm、大腿d₁长462 mm、小腿d₂长 393 mm。根据GB 10000—88《中国国家成年人人体尺寸》,由任意惯性参数可以计算该男子各段质量m₁=8.512 2 kg,m₂=2.552 6 kg,P是机器人自身的参数向量,其中参数 p₁=(m₁+m₂)d²₁,p₂=m₂d²₁,p₃=m₂d₁d₂,p₄=(m₁+m₂)d₁,p₅=m₂d₂, g=9.8 m/s²。可得两关节下肢康复机器人动力学模型^[11-12]中的参数为

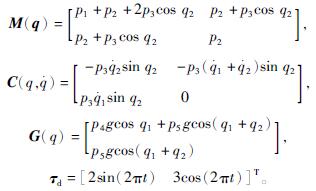
下肢康复机器人的两关节角度的理想指令取为

q_1d=cos t,q_2d=sin t,

系统的初始状态为

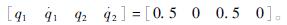
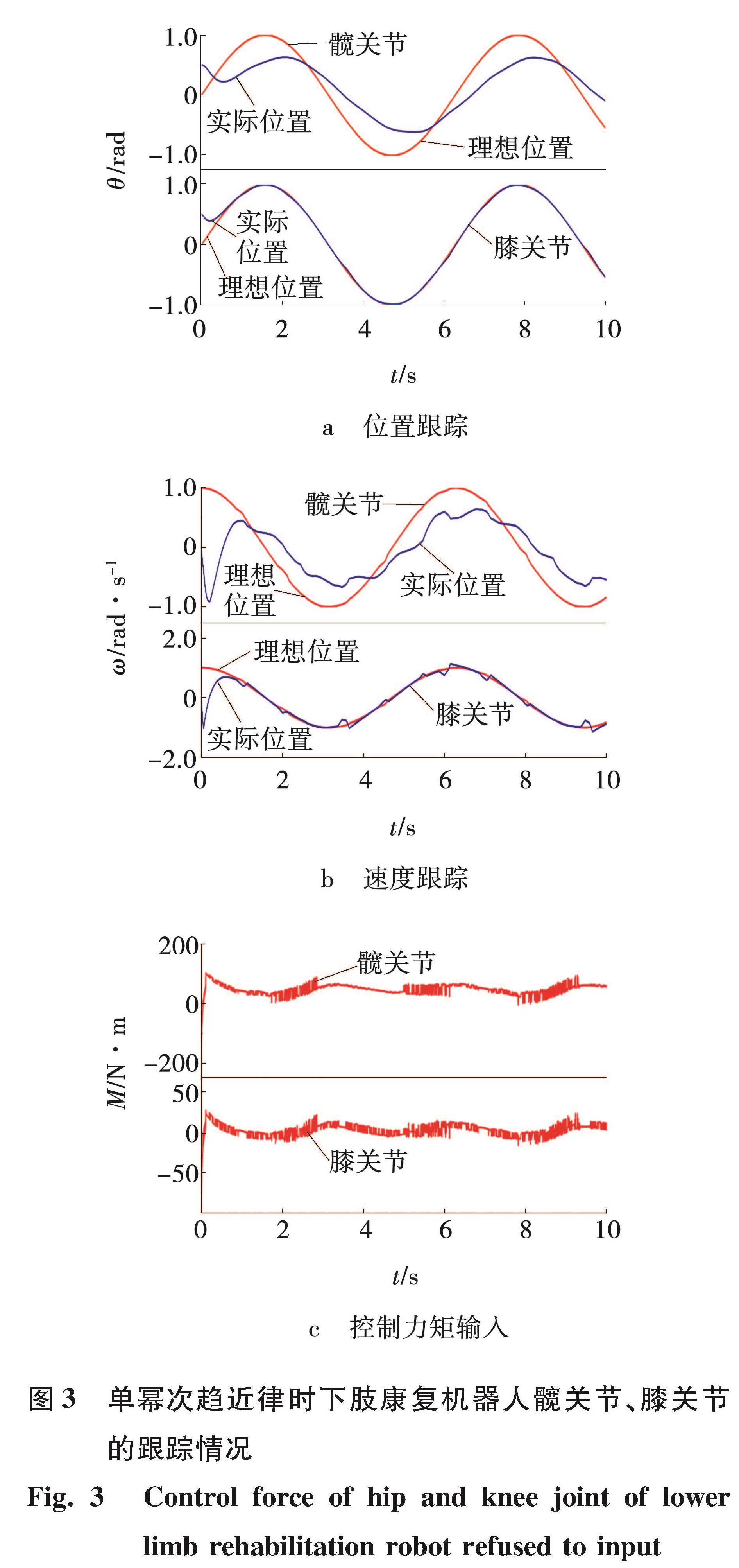
取c₁=c₂=0.5,k=3,K₁=1,K₂=3,α=0.2,β=3,对下肢康复机器人采用控制率(4)以及控制率(8)分别进行控制系统仿真分析。

采用经典的单幂次趋近律时,下肢康复机器人的位置、速度跟踪轨迹仿真图如图3所示。

由图3a、b可见,膝关节的跟踪可以达到理想的跟踪状态,但在膝关节的速度跟踪过程中出现了抖动现象。由于下肢康复机器人在运动过程中,髋关节的受力比较复杂,所以在利用单幂次趋近律滑模控制时,髋关节的跟踪效果明显没有达到理想的跟踪要求。从图3c控制输入的力矩来看,力矩输入具有明显的抖振现象。

图3 单幂次趋近律时下肢康复机器人髋关节、膝关节的跟踪情况
Fig.3 Control force of hip and knee joint of lower limb rehabilitation robot refused to input

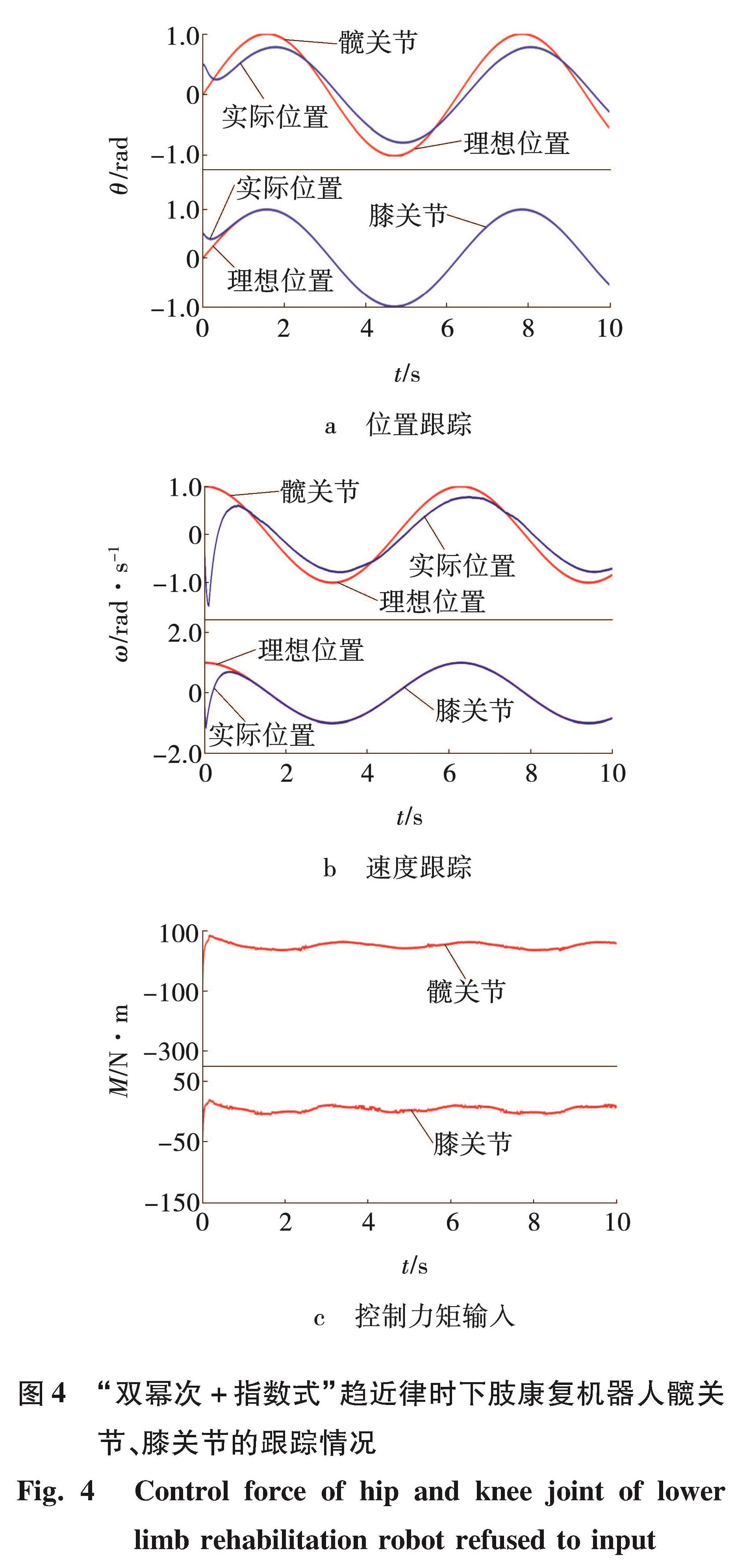
利用改进的“双幂次+指数式”趋近律后,下肢康复机器人的位置、速度跟踪轨迹仿真图如图4所示。

由图4a、b可见,膝关节的跟踪可以达到理想的跟踪状态,并且具有一定的稳定性。利用改进趋近律的滑模控制后,虽然髋关节的位置和速度的跟踪效果也没有达到理想的跟踪要求。但是相对于单幂次趋近律而言,在一定程度上提高了髋关节的跟踪精度。从图4c控制输入的力矩来看,采用改进“双幂次+指数式”趋近律的滑模控制,在一定程度上削弱了系统的抖振,提升了系统的稳定性。

图4 “双幂次+指数式”趋近律时下肢康复机器人髋关节、膝关节的跟踪情况
Fig.4 Control force of hip and knee joint of lower limb rehabilitation robot refused to input

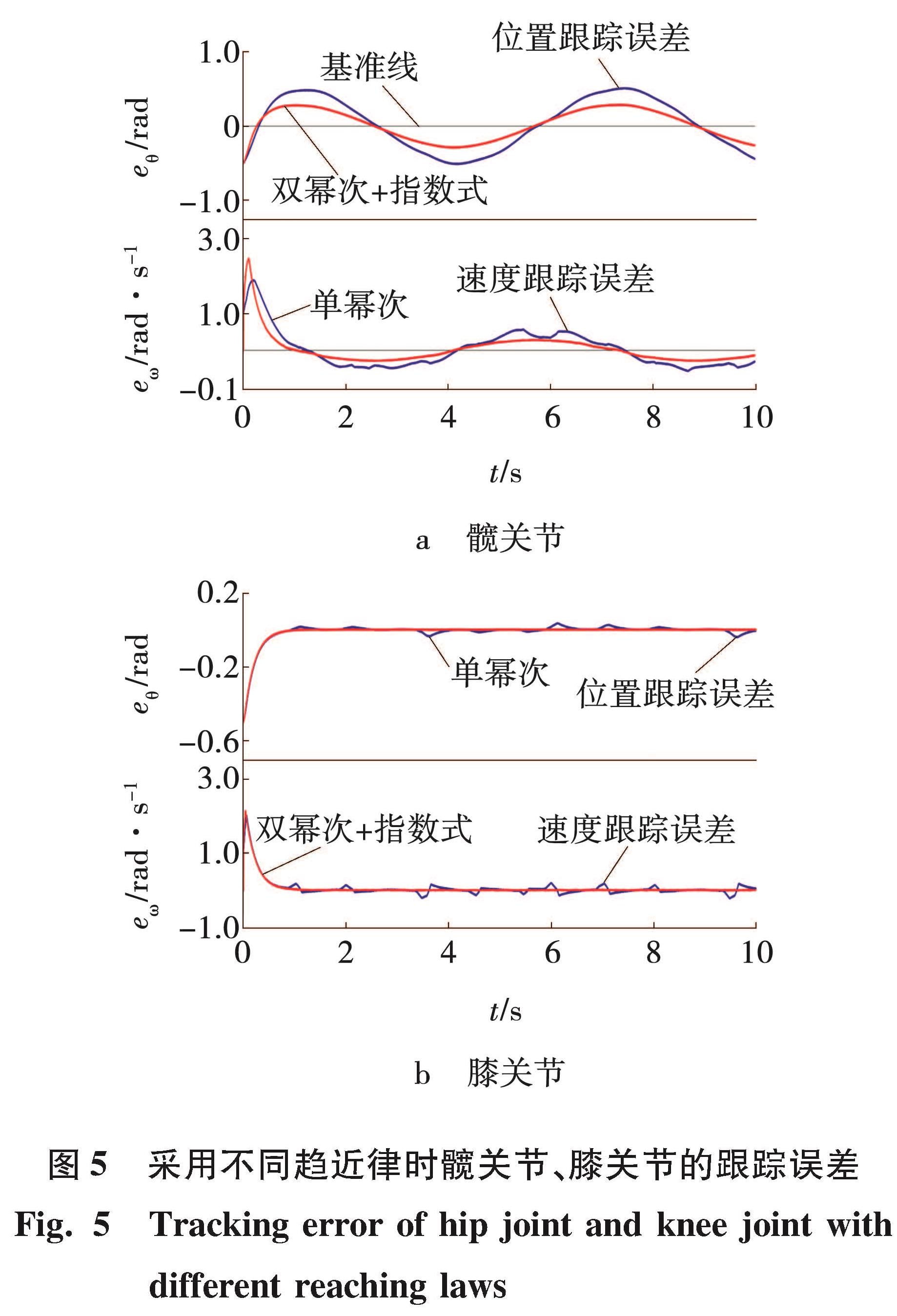
采用不同趋近律时,下肢康复机器人的位置与速度跟踪的误差分析如图5所示。

对下肢康复机器人采用两种不同趋近律的滑膜控制跟随误差进行对比,结果表明采用“双幂次+指数式”趋近律的滑模控制器时,明显缩小了跟踪的误差。从图5a可以看出控制初始时,采用“双幂次+指数式”趋近律滑模控制时,髋关节的速度误

图5 采用不同趋近律时髋关节、膝关节的跟踪误差
Fig.5 Tracking error of hip joint and knee joint with different reaching laws

差相对于单幂次趋近律而言较大,但是髋关节速度跟踪误差却能够在很短的时间内趋于稳定。说明在稳定性方面采用改进的趋近律的滑模控制要优于传统的单幂次趋近律滑模控制。图5b的对比可以看出,改进趋近律滑模控制的膝关节误差,随时间很快趋于平稳并且保持稳定状态,明显增强了系统的鲁棒性。

针对下肢康复机器人滑模控制系统存在抖振,以及在控制过程中因抖振问题产生的机器人跟随误差等问题,采用改进“双幂次+指数式”趋近律的方法,不仅削弱控制系统的抖振现象,而且提高了下肢康复机器人的跟踪精度以及控制系统的稳定性。通过Matlab/Simulink环境下的S函数对控制算法进行了仿真实验和对比分析可知,采用改进“双幂次+指数式”趋近律的方法设计的滑模控制系统,相对于传统的单幂次趋近律而言,具有良好的鲁棒性和控制精确度并且削弱了系统的抖振,具有一定的现实意义,为进一步研究下肢康复机器人提供了一些参考。