为分析双钢板-混凝土组合剪力墙筒体结构的抗震性能,利用ABAQUS有限元软件建立了轴压比分别为0.4、0.5、0.6、0.7的4个双钢板-混凝土组合剪力墙筒体模型,分析了不同轴压比下各剪力墙筒体的抗震性能、滞回曲线、骨架曲线、延性、刚度退化以及耗能能力。结果 表明:双钢板-混凝土组合剪力墙筒体具有很强的耗能能力; 轴压比越大,刚度退化速度越快; 轴压比为0.5时,双钢板-混凝土组合剪力墙筒体延性最好,累积耗能最多,具有良好的抗震性能。
This paper aims to analyze the double steel plate concrete composite shear wall square cylinder for the seismic performance. The study involves establishing four models with axial compression ratio of 0.4, 0.5, 0.6 and 0.7 using ABAQUS finite element software and analyzing the seismic performance, hysteretic curve, skeleton curve, ductility, stiffness degradation, and energy dissipation capacity of each shear wall square cylinder under different axial compression ratio. The results show that the double steel plate concrete composite shear wall square cylinder demonstrates a strong energy dissipation capacity; the larger the axial compression ratio is, the faster the stiffness degradation is; and the axial compression ratio( 0.5)gives the double steel plate concrete composite shear wall square cylinder the best ductility, the most cumulative energy consumption,and a better seismic performance.
双钢板-混凝土组合剪力墙以其优异的抗震性能,使得越来越多的国内学者对其展开实验研究。如聂建国等[1-2]、曹万林等[3]、夏登荣等[4]证明双钢板混凝土组合剪力墙具有优异的耗能能力。而筒体结构同样以其优异的抗震性能被广泛应用[5-6],考虑在建筑物中央区域利用电梯间、楼梯间或者洗手间围成的筒体结构作为建筑物主要的抗侧力结构,笔者将双钢板-混凝土组合剪力墙围成筒体结构,形成双钢板-混凝土组合剪力墙筒体,分析轴压比对双钢板-混凝土组合剪力墙筒体抗震性能的影响。
1 有限元模型验证本文依据文献[7-8]建立有限元验证模型,利用ABAQUS有限元软件建立与实验模型DCSW1尺寸完全相同的模型DCSW1-1,钢板采用S4R壳单元,混凝土采用C3D8R实体单元,见图1。钢板与混凝土之间为黏结滑移关系,法向接触为硬接触,切向接触为罚接触,侧向摩擦因数为0.25,底部摩擦
图1 有限元模型与实验试件
Fig.1 Finite element model and test piece因数为0.6。模型底板边界条件为完全固定,顶部中央设置参考点RP-1,并将其与顶面耦合,将竖向集中力3 719 kN与水平位移施加在参考点上。
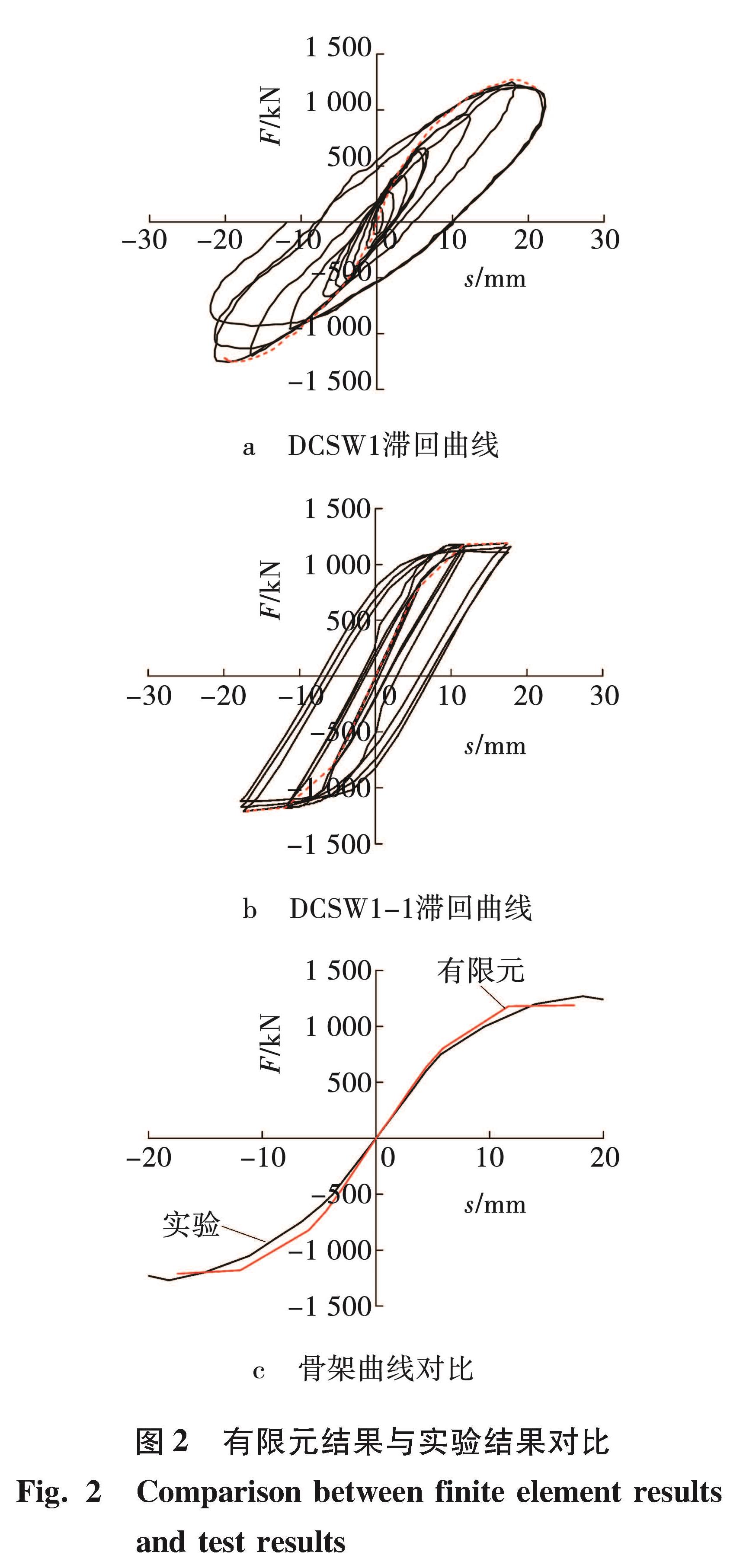
根据有限元验证模型计算结果与实验结果对比(图2)、破坏形式对比(图3)得出:两者破坏形式基本一致,均为构件底部混凝土压碎,并于每两个隔板之间出现鼓曲变形。两者骨架曲线形状相似,初始弹性刚度有限元构件略高,误差为1.75%; 弹塑性阶段有限元构件屈服荷载与屈服位移均高于实验构件,误差分别为8.16%、2.48%; 有限元构件峰值荷载与峰值位移均低于实验构件,误差分别为5.51%、4.23%。误差产生的原因:验证模型中的材料被认为是均匀的,构件无初始缺陷,钢板连接无缺陷,而实际实验构件的材料、构件的连接存在缺陷。通过验证模型计算结果与实验结果对比可以得出,使用ABAQUS能够较准确的模拟双钢板混凝土组合剪力墙在往复荷载作用下的滞回性能。
2 有限元模型的建立
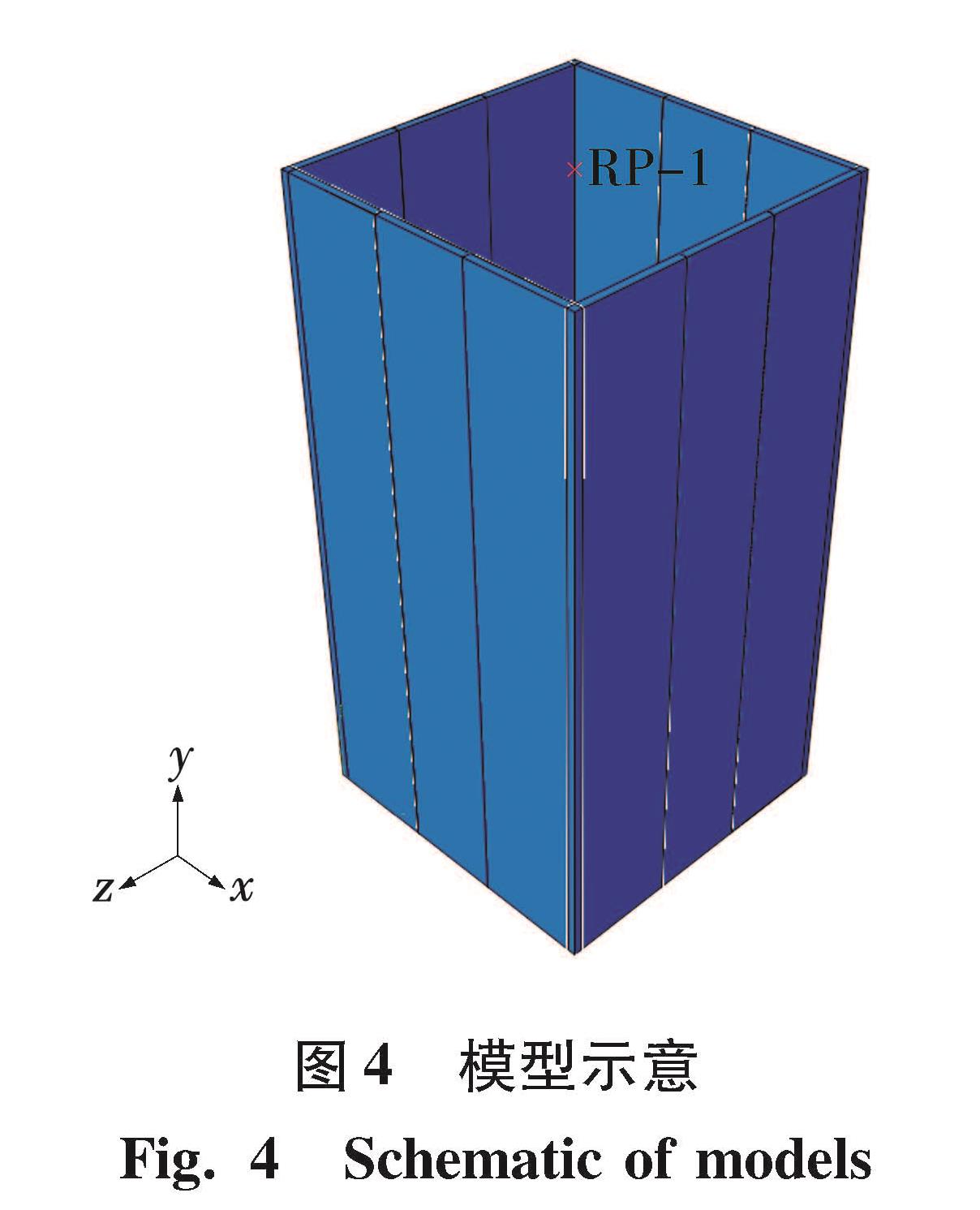
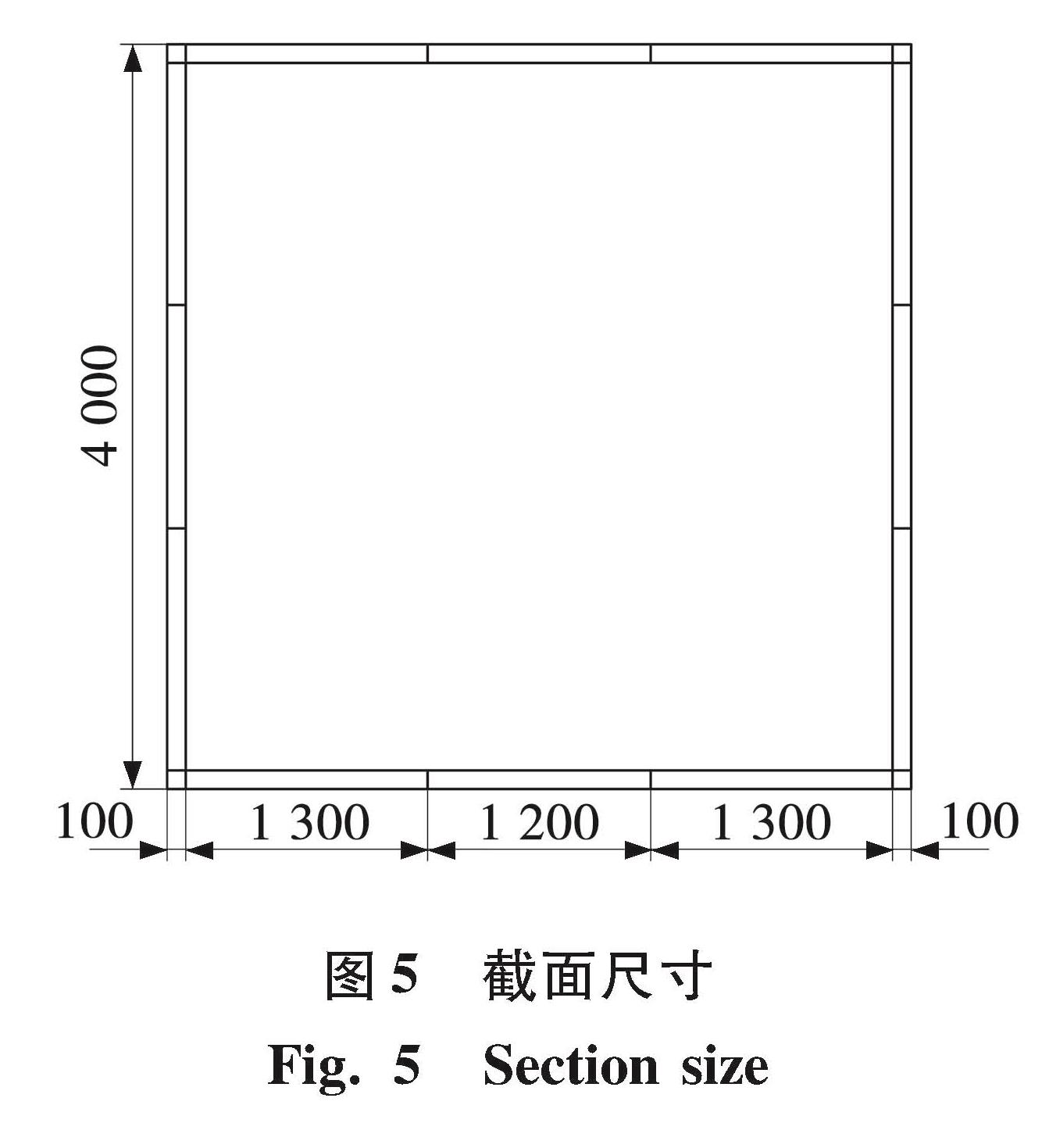
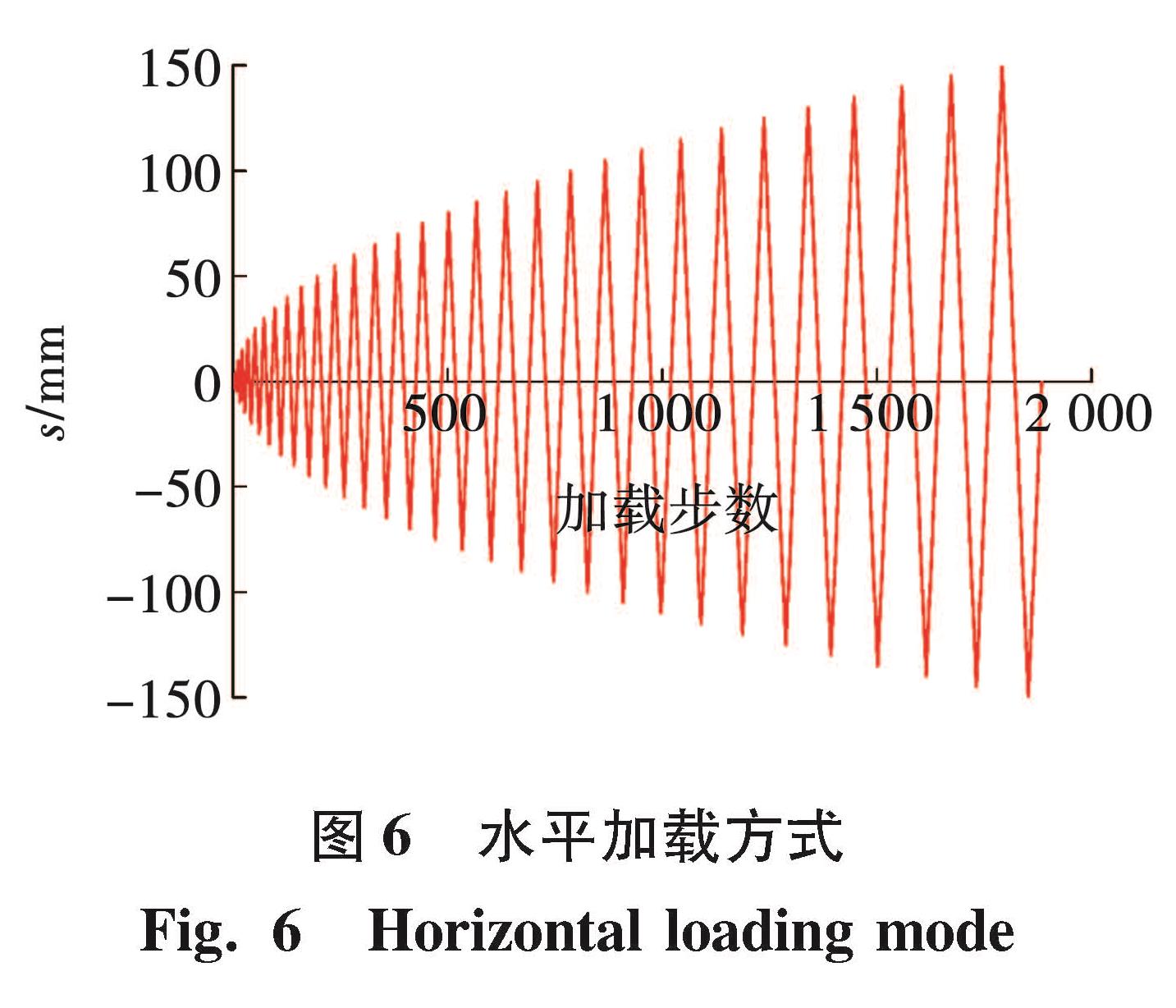
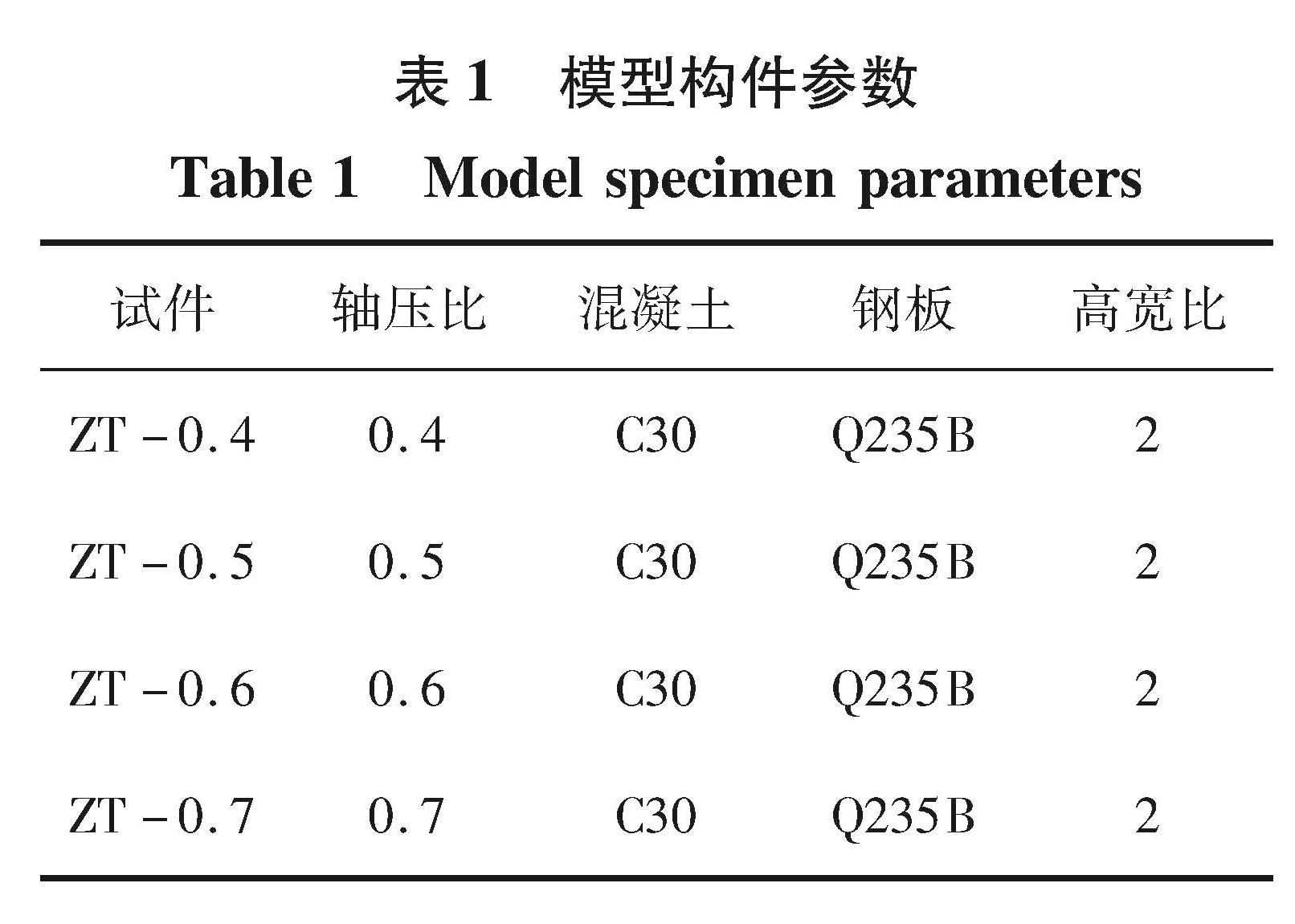
使用ABAQUS有限元分析软件建立双钢板-混凝土组合剪力墙筒体模型ZT-0.4,钢板采用S4R壳单元,混凝土采用C3D8R实体单元。模型ZT-0.4尺寸:高度8 000 mm,墙厚100 mm,筒体横截面为4 000 mm×4 000 mm,外包钢板厚度10 mm,采用隔板连接,模型示意图见图4,截面尺寸见图5。模型轴压比为0.4,边界条件为底部完全固定,钢板与混凝土之间接触为切向罚接触,摩擦因数0.25,法向硬接触,钢材、混凝土本构模型均与验证模型相同,顶部中央设置参考点RP-1,并将其与顶面耦合,将竖向集中力与水平位移施加在参考点上,水平加载方式见图6。在模型ZT-0.4基础上,仅改变轴压比大小建立模型ZT-0.5、ZT-0.6、ZT-0.7。ZT系列模型具体参数见表1。
3 有限元结果与滞回性能3.1 滞回曲线与骨架曲线
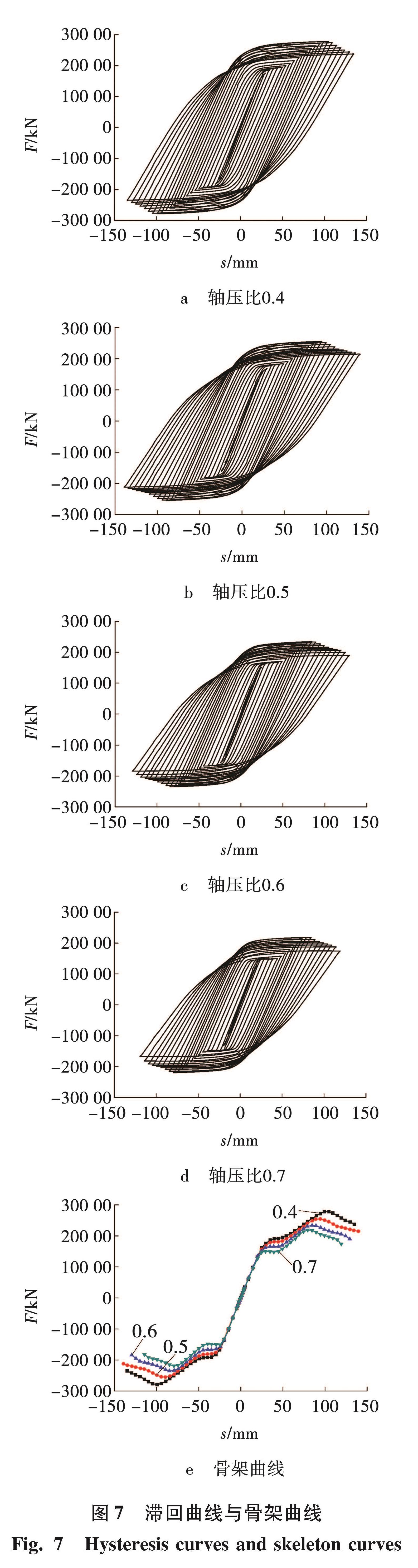
图7所示为ZT系列模型荷载-位移滞回曲线与荷载-位移骨架曲线。从图中可以看出,双钢板-混凝土组合剪力墙筒体在轴压比分别为0.4、0.5、0.6、0.7时,滞回曲线都很饱满,滞回环呈梭形,说明双钢板-混凝土组合剪力墙筒体耗能能力较强。随着轴压比的增大,滞回曲线形状越来越扁平。将各轴压比下滞回曲线每次循环加载的峰值点依次连接形成骨架曲线,可以看出:各轴压比下骨架曲线形状相似,弹性阶段基本重合; 但轴压比越大,骨架曲线拐点出现越早,说明试件进入弹塑性阶段越早,同时峰值荷载越小,极限荷载越小。
3.2 承载力与变形能力
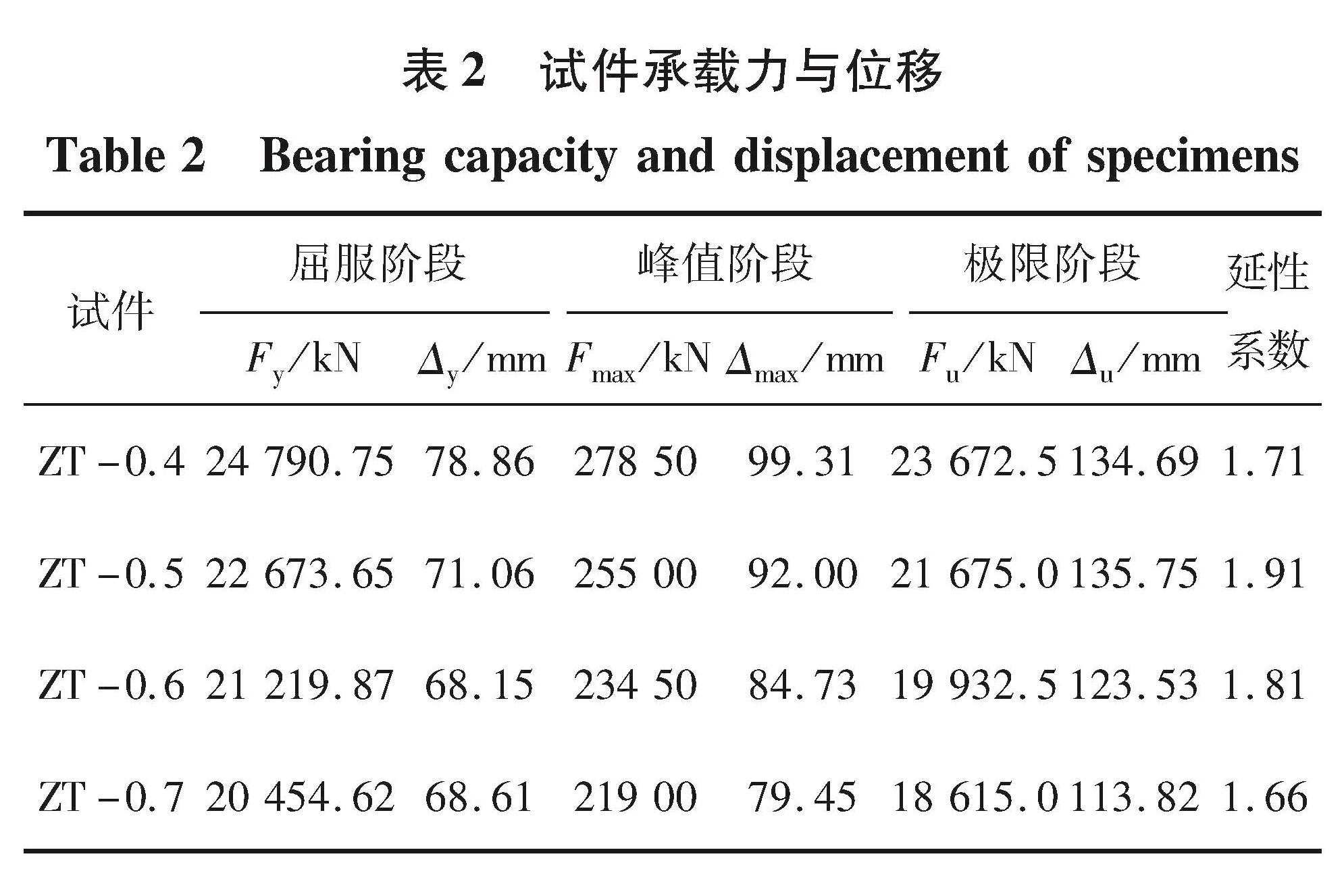
表2给出了ZT系列模型承载力F与变形Δ的具体数值。利用骨架曲线,采用割线刚度法计算屈服点,将水平荷载最大值点确定为峰值点,取峰值荷载下降85%为极限点。延性系数为极限位移与屈服位移的比值[9]。
由表2可知,随着轴压比的增大,试件屈服荷载、峰值荷载、极限荷载、峰值位移逐渐降低。ZT-0.7与ZT-0.6相比,峰值荷载降低了7.08%,峰值位移降低了6.65%; ZT-0.6与ZT-0.5相比,峰值荷载降低了8.74%,峰值位移降低了8.58%; ZT-0.5与ZT-0.4相比,峰值荷载降低了9.22%,峰值位移降低了7.95%,说明轴压比越大,试件承载力越小,达到峰值荷载的变形也越小。对比延性系数可知,当轴压比由0.4升至0.5时,延性系数增大11.70%,轴压比为0.5时,试件延性系数最大,当轴压比由0.5升至0.6、0.6升至0.7时,延性系数分别减小5.24%、8.29%,说明轴压比为0.5时,试件变形能力较好,当轴压比超过0.5时,试件变形能力逐渐变弱。
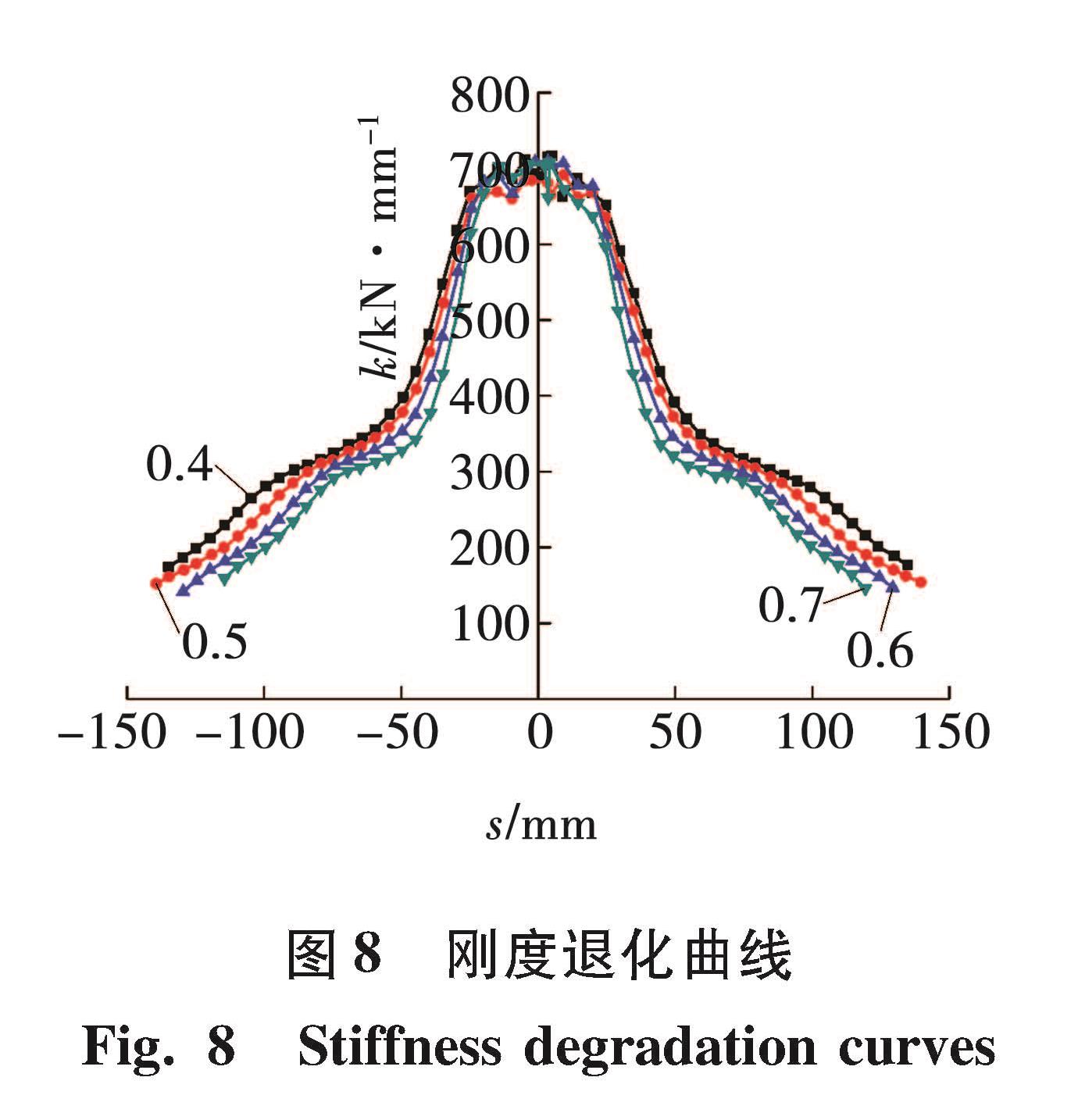
3.3 刚度退化将荷载-位移滞回曲线每次循环加载的峰值点荷载与峰值点位移的比值顺次连接,得到刚度退化曲线。图8给出各轴压比下的刚度退化曲线,从图8可以看出:各轴压比下刚度退化曲线形状相似,左右对称; 在弹性阶段,由于初始施加水平位移较小,往复作用下刚度值有波动; 随着施加的水平位移逐渐增大,各轴压比下刚度退化曲线变得平缓; 轴压比越大,试件在超出弹性阶段后的刚度退化速度越快; 在试件达到极限点时,轴压比为0.4的试件刚度最大,轴压比为0.5、0.6、0.7的试件刚度相差不大,但均比轴压比为0.4时刚度小。
3.4 耗能能力
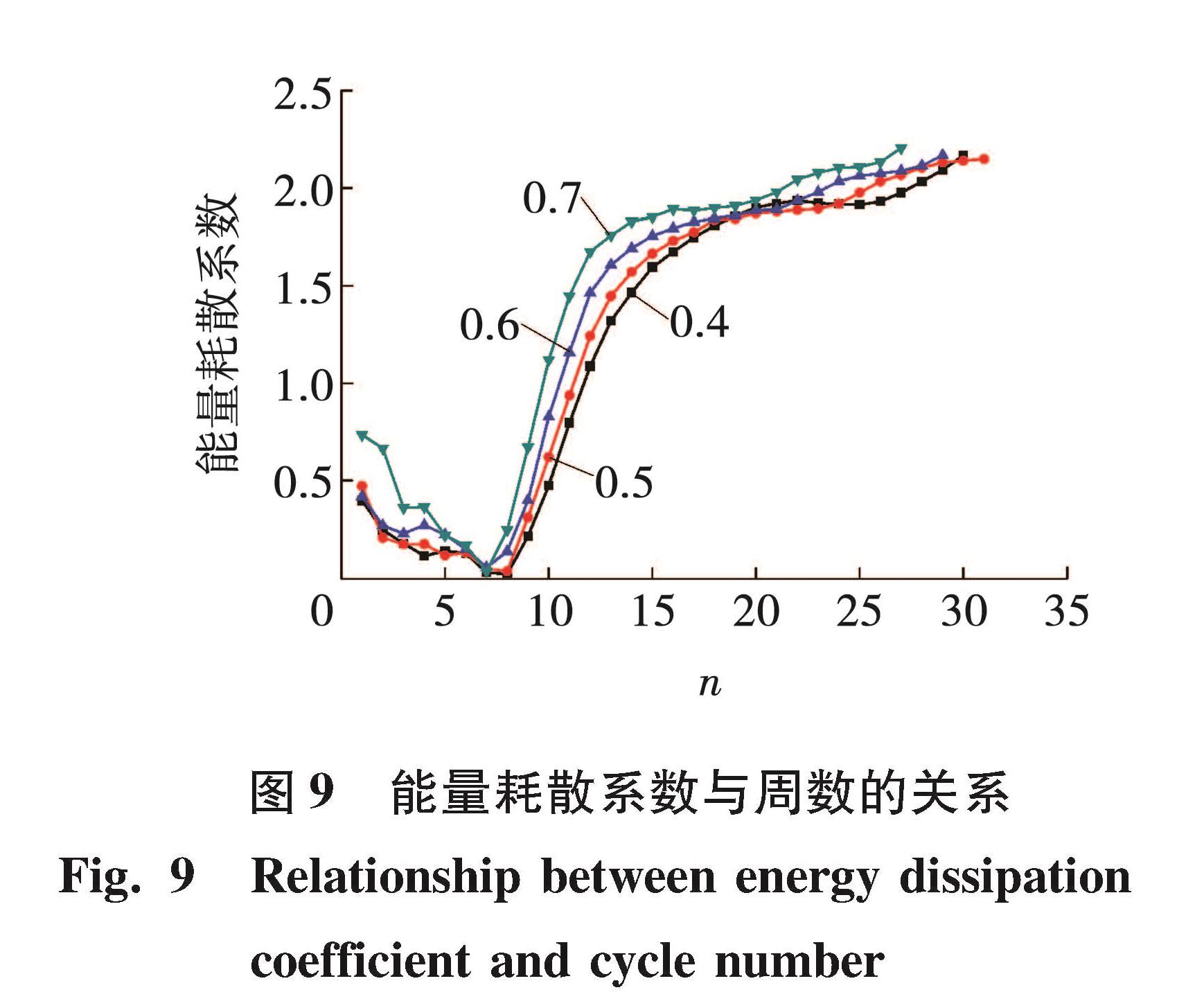
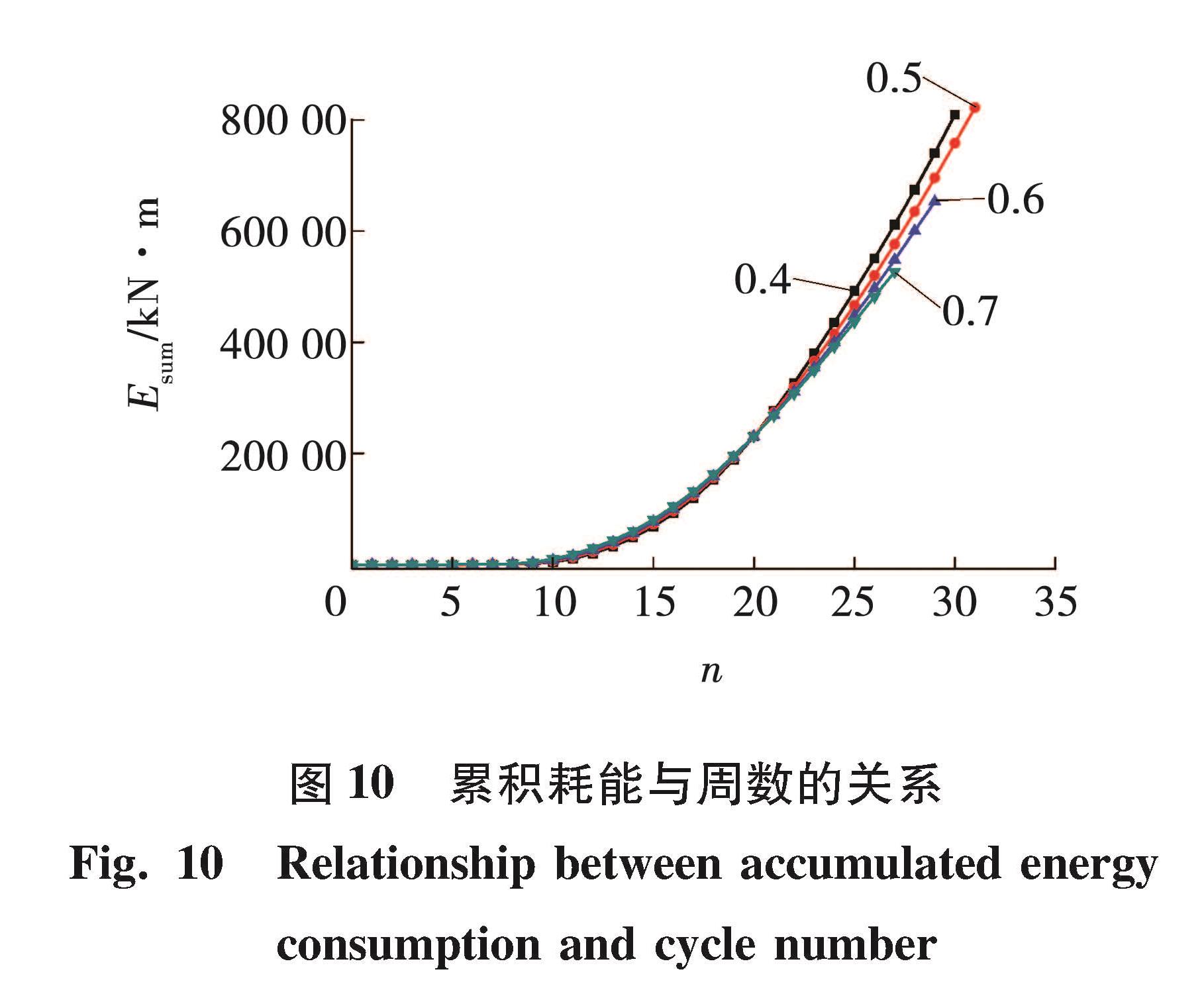
根据所得各轴压比下荷载-位移滞回曲线计算出各构件每周的能量耗散,绘制出各轴压比下能量耗散系数-周数n、累积耗能-周数n的变化曲线,用来表示各构件的耗能能力[1]。能量耗散系数-周数n曲线见图9,累积耗能-周数n曲线见图 10。
由图9可以看出,各轴压比下双钢板-混凝土组合剪力墙筒体试件能量耗散系数-周数n曲线形状相似; 当周数8≤n≤18时,相同周数中试件轴压比越大,能量耗散系数越大,说明试件在弹塑性阶段且水平位移相同时,轴压比越大试件耗能能力越强; 当周数19≤n≤22时,相同周数中轴压比为0.4的试件能量耗散系数略大于轴压比为0.5、0.6的试件,轴压比为0.7的试件能量耗散系数最大; 当周数n=23时,轴压比为0.5的试件能量耗散系数最小,轴压比为0.7的试件能量耗散系数最大; 当周数24≤n≤27时,相同周数中轴压比越大的试件能量耗散系数越大,说明试件在塑性阶段且水平位移相同时,轴压比越大试件耗能能力越强; 当周数n>27时,轴压比为0.7的试件已退出工作,轴压比为0.4、0.5、0.6的试件继续耗能直至退出工作。
由图 10可以看出,各轴压比下双钢板-混凝土组合剪力墙筒体试件累积耗能-周数n曲线形状相似; 当周数n≤21时,累积耗能曲线基本重合; 当周数22≤n≤27时,相同周数中轴压比越小的试件累积耗能越多; 当周数n>27时,轴压比为0.7的试件已退出工作,轴压比为0.4、0.5、0.6的试件继续耗能直至退出工作。对比各轴压比下试件的累积耗能量,当轴压比由0.4升至0.5时,试件累积耗能增大1.59%,当轴压比由0.5升至0.6、0.6升至0.7时,试件累积耗能分别减小20.60%、19.29%,说明试件轴压比为0.5时,试件累积耗能最多,与试件延性系数随轴压比的变化趋势相同,说明试件延性越好,累积耗能能力越强。
4 结 论(1)对双钢板-混凝土组合剪力墙筒体,轴压比越大,试件承载力越小,达到峰值荷载的变形越小。对于本文模型,当轴压比为0.5时,试件变形能力较好,当轴压比超过0.5时,试件变形能力逐渐变弱。
(2)各轴压比下试件刚度退化曲线形状相似,但轴压比越大,试件在超出弹性阶段后的刚度退化速度越快。
(3)各轴压比下试件的滞回曲线都很饱满,滞回环呈梭形,说明双钢板-混凝土组合剪力墙筒体耗能能力较强。试件在弹塑性阶段且水平位移相同时,轴压比越大试件耗能能力越强。对于本文模型,轴压比为0.5的试件延性最好,同时试件累积耗能最多。
- [1] 聂建国, 卜凡民, 樊健生. 高轴压比、低剪跨比双钢板-混凝土组合剪力墙拟静力试验研究[J]. 工程力学, 2013, 30(6): 60-66.
- [2] 汪家继, 樊健生, 陶慕轩, 等. 中高剪跨比双钢板-混凝土组合剪力墙受力性能有限元分析[J]. 建筑结构学报, 2015, 36(S2): 1-8.
- [3] 郝婷玥, 曹万林. 双钢板混凝土组合剪力墙轴压承载力研究[J]. 工程科学学报, 2017, 39(11): 1765-1773.
- [4] 夏登荣, 陈丽华, 吴晓枫, 等. 不同连接构造双钢板混凝土组合剪力墙试验研究[J]. 建筑结构, 2019(14): 36-41.
- [5] 孙建伟. 框架-混合筒体抗震性能试验研究与分析[D]. 长沙: 中南大学, 2010.
- [6] 陈 兵. 带混合暗支撑的钢筋混凝土双室筒体力学性能研究[D]. 长沙: 湖南大学, 2015.
- [7] 邱丽秋. 开洞双层钢板内填混凝土剪力墙的抗震性能试验研究[D]. 上海: 同济大学, 2014.
- [8] 郭小农, 邱丽秋, 罗永峰, 等. 开洞双钢板组合剪力墙抗震性能试验[J]. 哈尔滨工业大学学报, 2015, 47(6): 69-76.
- [9] 冯榆晟, 伍云天, 胡逸轩, 等. 钢板混凝土联肢剪力墙子结构抗震性能试验研究[J]. 建筑结构学报, 2019(S1): 18-30.
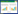 图 1 有限元模型与实验试件
Fig.1 Finite element model and test piece因数为0.6。模型底板边界条件为完全固定,顶部中央设置参考点RP-1,并将其与顶面耦合,将竖向集中力3 719 kN与水平位移施加在参考点上。
图 1 有限元模型与实验试件
Fig.1 Finite element model and test piece因数为0.6。模型底板边界条件为完全固定,顶部中央设置参考点RP-1,并将其与顶面耦合,将竖向集中力3 719 kN与水平位移施加在参考点上。