东荣二矿是黑龙江龙煤双鸭山矿业有限责任公司所属生产矿井。随着煤田高强度开采,开采深度已达到850 m,并且采掘工作逐步向深部和地质条件更复杂的区域转移,支护问题越发难以解决。
国内外学者对巷道支护方面问题进行了大量的研究,得出充分发挥支护的作用能使巷道围岩变形得到有效的减小[1-2],其中锚杆在煤矿巷道支护中占主要地位[3-4]。孙守孝[5]基于理论计算对锚杆和锚索间排距进行了优化,解决了巷道支护密度大及支护成本高的问题。侯兴[6]采用高强度及高预紧力锚杆对巷道围岩进行控制支护,保障了近距离下煤层巷道的稳定。Wang等[7]指出,巷道围岩在应力重新分布时变形发展速度较快,且伴有流变性。并通过案例说明了多种相互联系的支护方式对软岩巷道支护可以起到良好的效果。Shan等[8]通过现场监测验证提出了“三步走”支护理论方案的可行性。张志强[9]研究了掘进巷道围岩变形破坏机理及锚注联合支护技术,为掘进巷道的稳定和支护提供参考。穆磊等[10]借助FLAC3D对不同的锚杆长度和排距进行分析,得出了最优长度和最优排距。
笔者采用理论分析和数值模拟相结合的方法,以东荣二矿围岩变形问题为研究对象,对南二下采区回风下山巷道支护参数展开研究,从锚杆的间排距及预应力的角度确定出巷道围岩支护的最优解决方案。
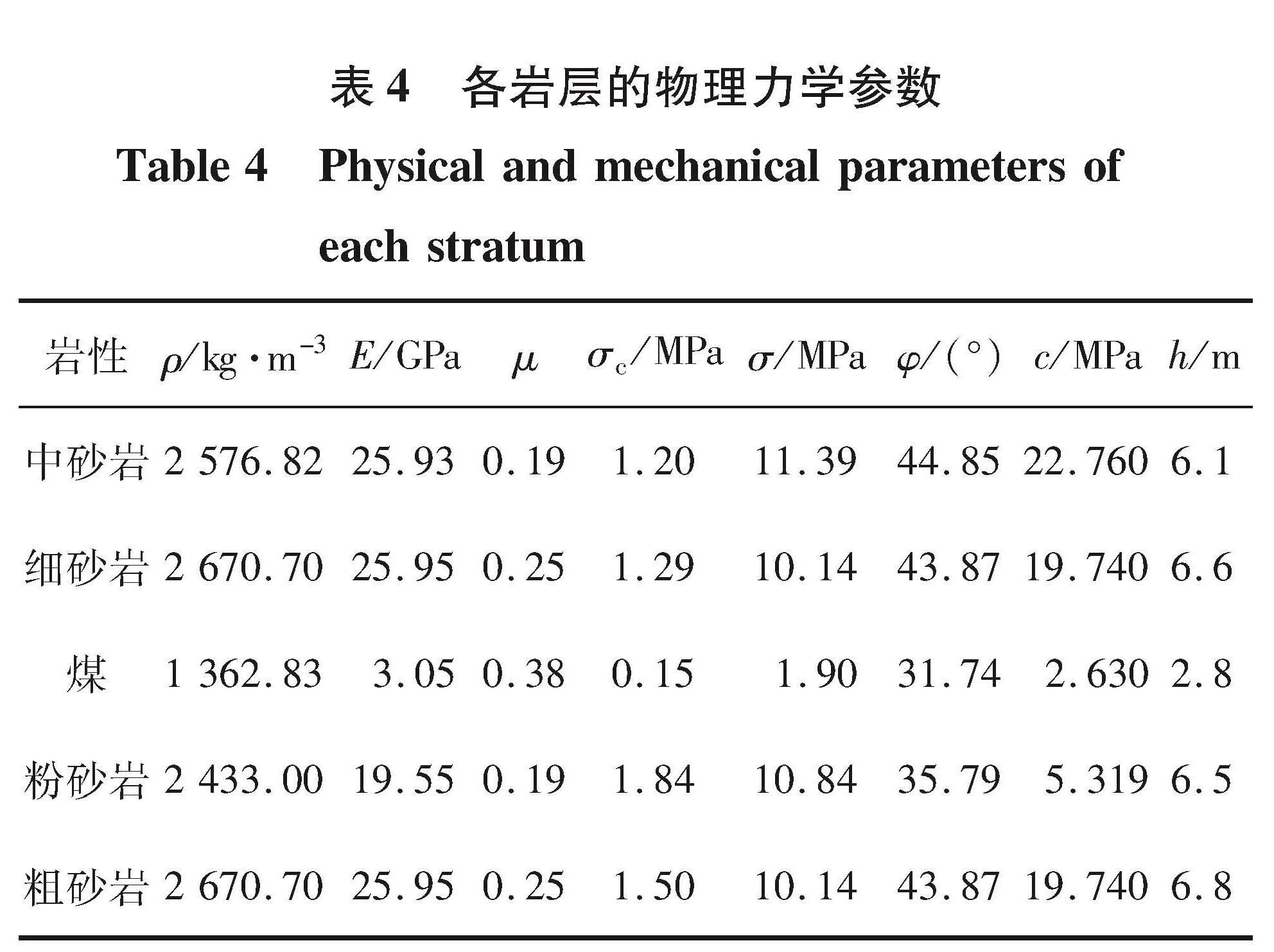
1 工程概况该回风下山巷道埋深在800~900 m,开采南二下采区16煤层,平均厚2.8 m。煤层总体为一单斜构造区,地层走向NS,倾向W,倾角最小16°,最大22°,平均19°。开采煤层无直接顶,基本顶为6.6 m左右的细砂岩,其上部存在一层厚约6.1 m的中砂岩; 无直接底,基本底为6.5 m左右的粉砂岩,其下部存在一层厚约6.8 m的粗砂岩。
该巷道是采用工程类比法进行巷道支护设计的。在一些破碎地带采用了锚杆加金属网支护,整体支护效果一般,大部分巷道均不同程度出现顶板、两帮失稳现象。分析总结东荣二矿巷道变形情况,巷道表现出掘进期间受断层等特殊地质影响,巷道收敛明显且变形量大,围岩中的应力集中程度较大,巷道支护困难且效率低、成本高。工作面的超前支承压力和侧向支承压力峰值高,上覆岩层冒落高度和断裂带高度大,严重扰动前方回采巷道稳定性,随着工作面的回采,巷道支护难度进一步加剧。
2 巷道围岩塑性破坏能与支护力的关系由塑性破坏能在巷道围岩中的的表达式(1)[11]可以得出,围岩的力学参数和巷道尺寸不变时,式中系数均为常数,由于塑性破坏的能量Up是关于A也就是支护力pz的函数,可见,巷道在开挖过程中塑性破坏能和支护力密切相关。
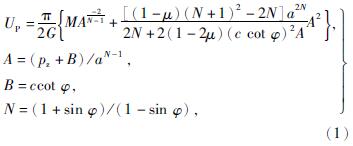
式中:c——黏聚力;
φ——内摩擦角;
μ——泊松比;
M、G——N、c、φ、μ的常数;
a——常数。
在此基础上,以东荣二矿南二下采区16号煤层回风下山巷道的基本参数进行研究,得出巷道开挖后,在不同支护力、不同围岩参数下巷道围岩内塑性破坏能的变化情况,进而分析它们之间的关系。该巷道所处地层为粉砂岩,相关力学参数见表1。
将各个参数代入式(1),得出:
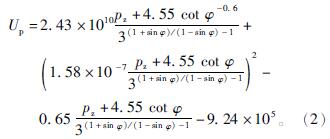
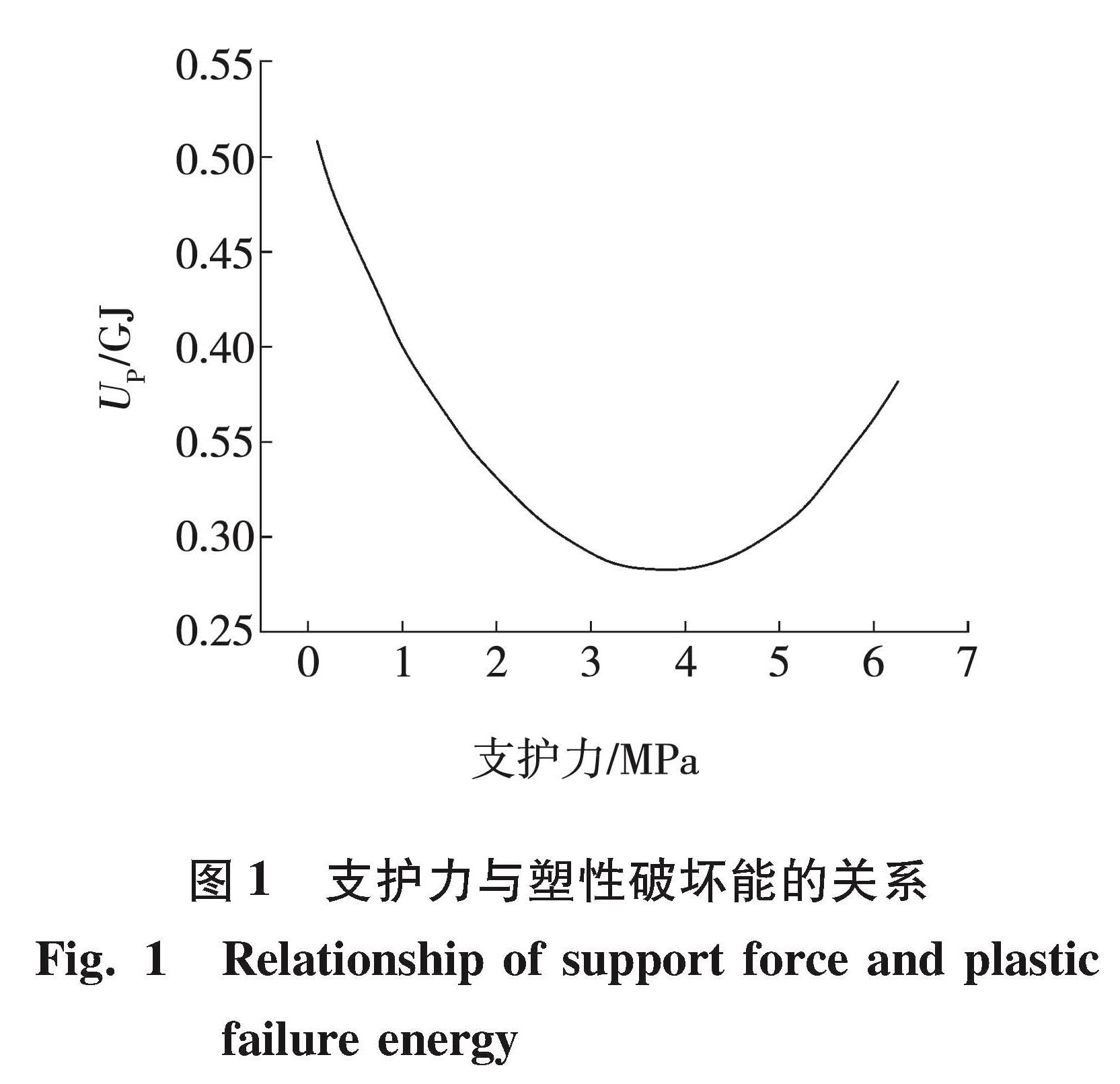
支护力与塑性破坏能的关系见图1。巷道围岩塑性破坏能随支护力的增加呈减小的趋势,当支护力为3.5 MPa时,塑性破坏能达到了临界值; 继续加大支护力,巷道围岩内的塑性破坏能开始增加。由此可以得出,支护结构的支护力存在极限值,塑性破坏能随着支护力的增加呈先减小后增大的趋势,在极限值之前,支护力可以降低岩体内部塑性破坏能,但对塑性破坏能的积聚没有影响。在工程中支护结构的支护力往往很小,不会超过支护力的极限值,可以吸收一部分塑性破坏能,减少巷道围岩的位移,因此适当加大支护力使其塑性破坏能接近临界值可以维持巷道围岩的稳定。
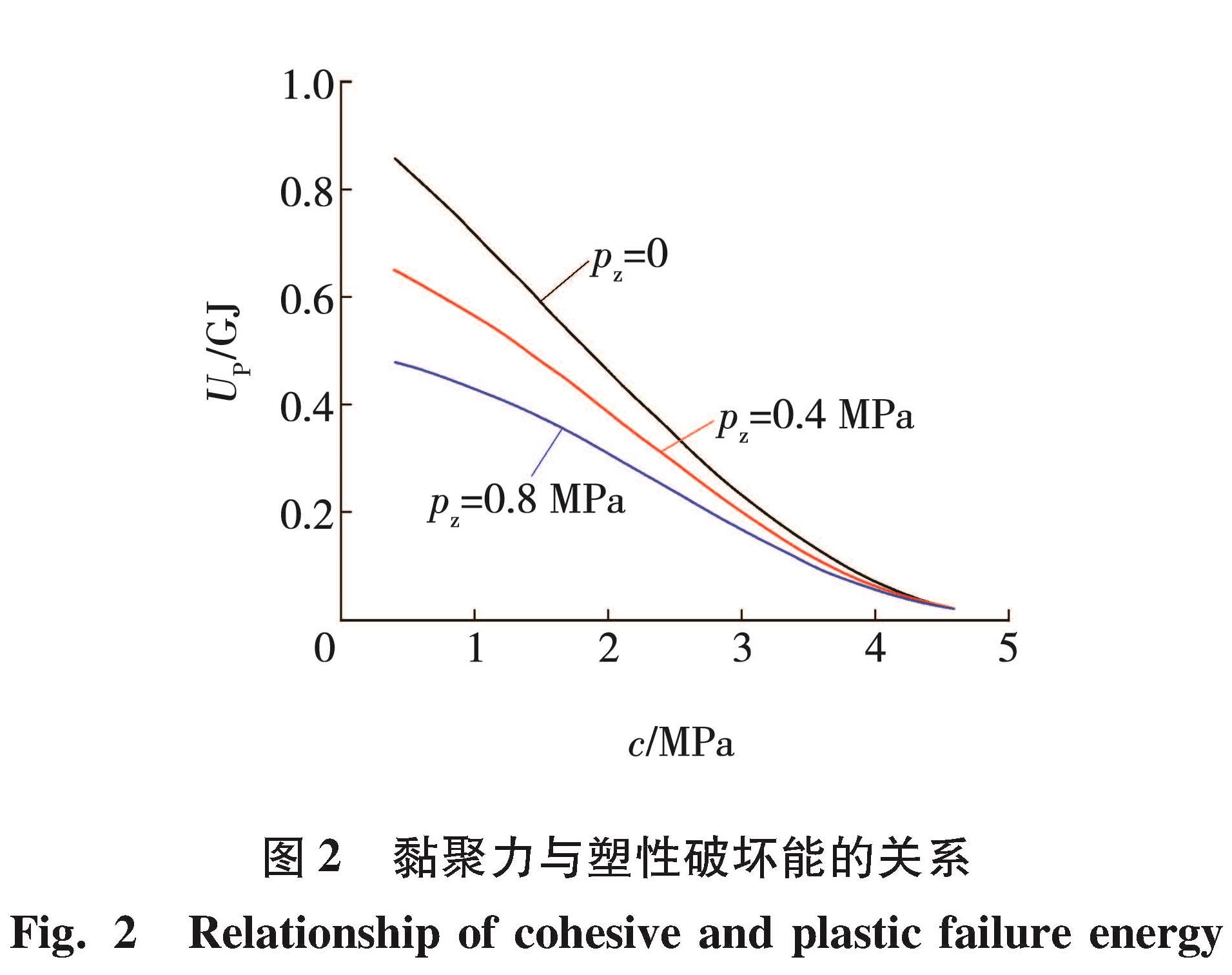
黏聚力与塑性破坏能的关系见图2。由图2可知,巷道围岩内塑性破坏能随黏聚力的增大呈减少趋势。
当黏聚力在1.0~3.5 MPa期间,塑性破坏能不断下降,且下降趋势较大,说明此阶段黏聚力对塑性破坏能的影响较大。当黏聚力增加到3.5 MPa之后,塑性破坏能的下降速度明显变缓。从图2中还发现,在3种不同大小的支护力下,黏聚力对巷道塑性破坏能的影响变化趋势不同,在黏聚力由1.0 MPa增加到3.0 MPa过程中,支护力的大小对塑性破坏能的影响比较明显。随着黏聚力的继续增大,不同支护力对吸收巷道围岩塑性破坏能的大小基本达到一致,若此时想再降低巷道围岩内的塑性破坏能,不应该选取增加支护力的方式。
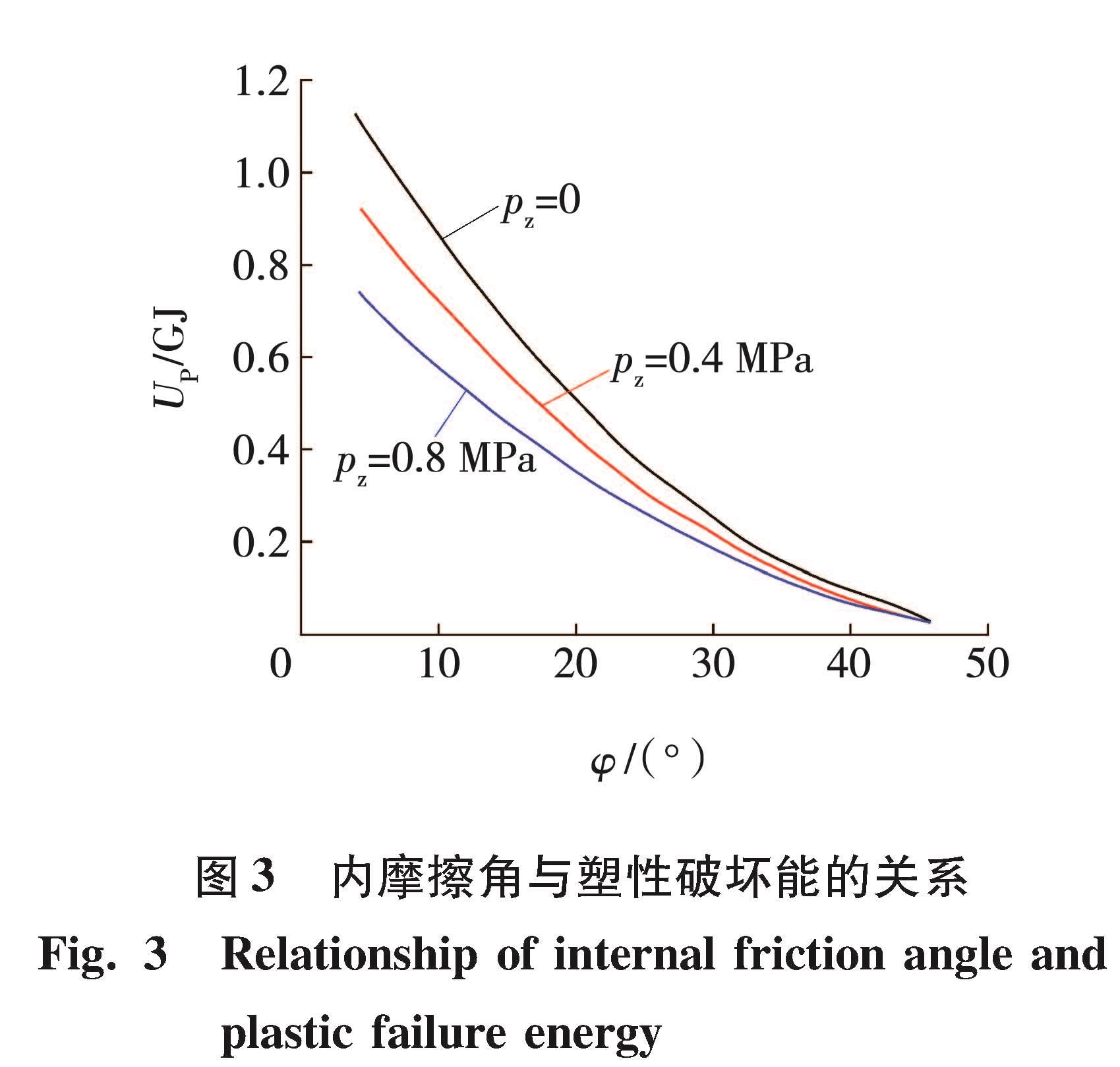
内摩擦角与巷道围岩塑性破坏能的关系见图3。随着内摩擦角的增大,塑性破坏能逐渐减小,且塑性破坏能在一定范围内呈直线下降,与黏聚力的变化规律相同,同时还可以发现,随着支护力的增加,巷道围岩塑性破坏能逐渐减小。当内摩擦角小于30°时,巷道围岩塑性破坏能受支护力的大小影响明显,说明巷道围岩内摩擦角较小时,支护对巷道围岩的变形破坏起到很好的控制作用。内摩擦角增加到30°以后,对应的塑性破坏能之间的值相差不大,巷道围岩吸收塑性破坏能的大小基本一致。
3 支护参数对围岩区力学性质的影响
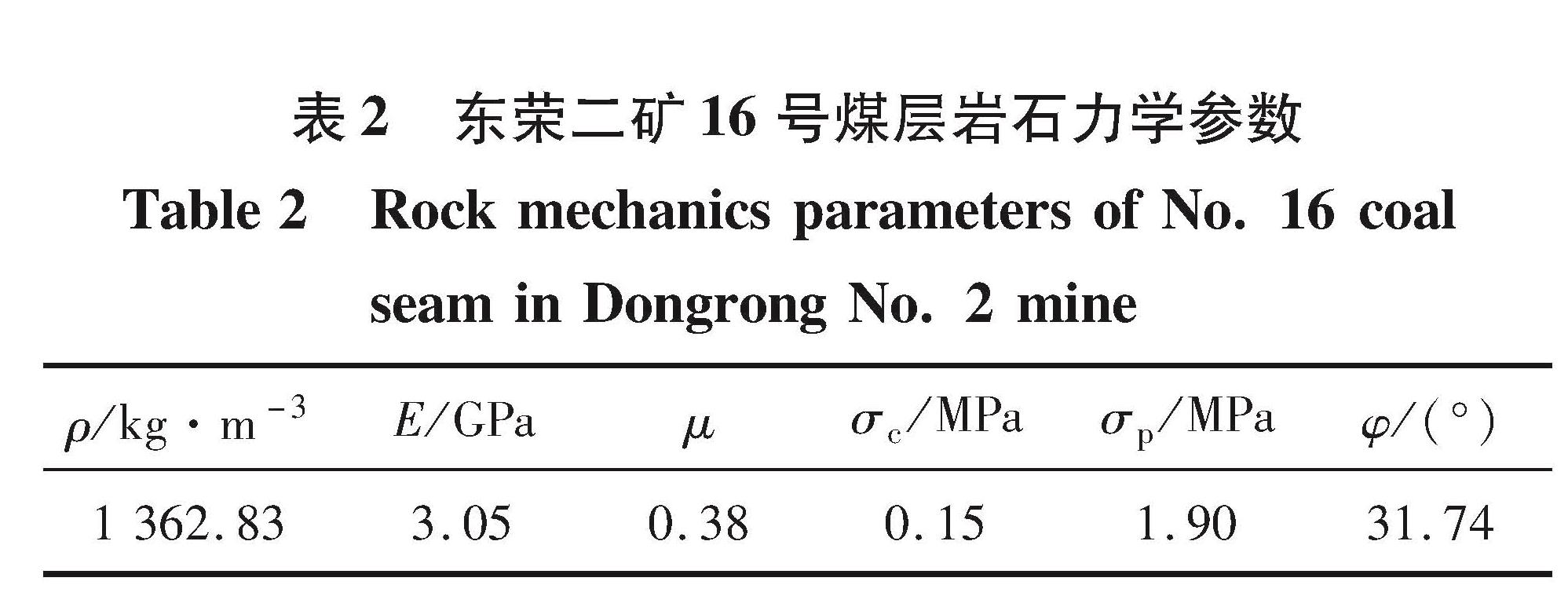
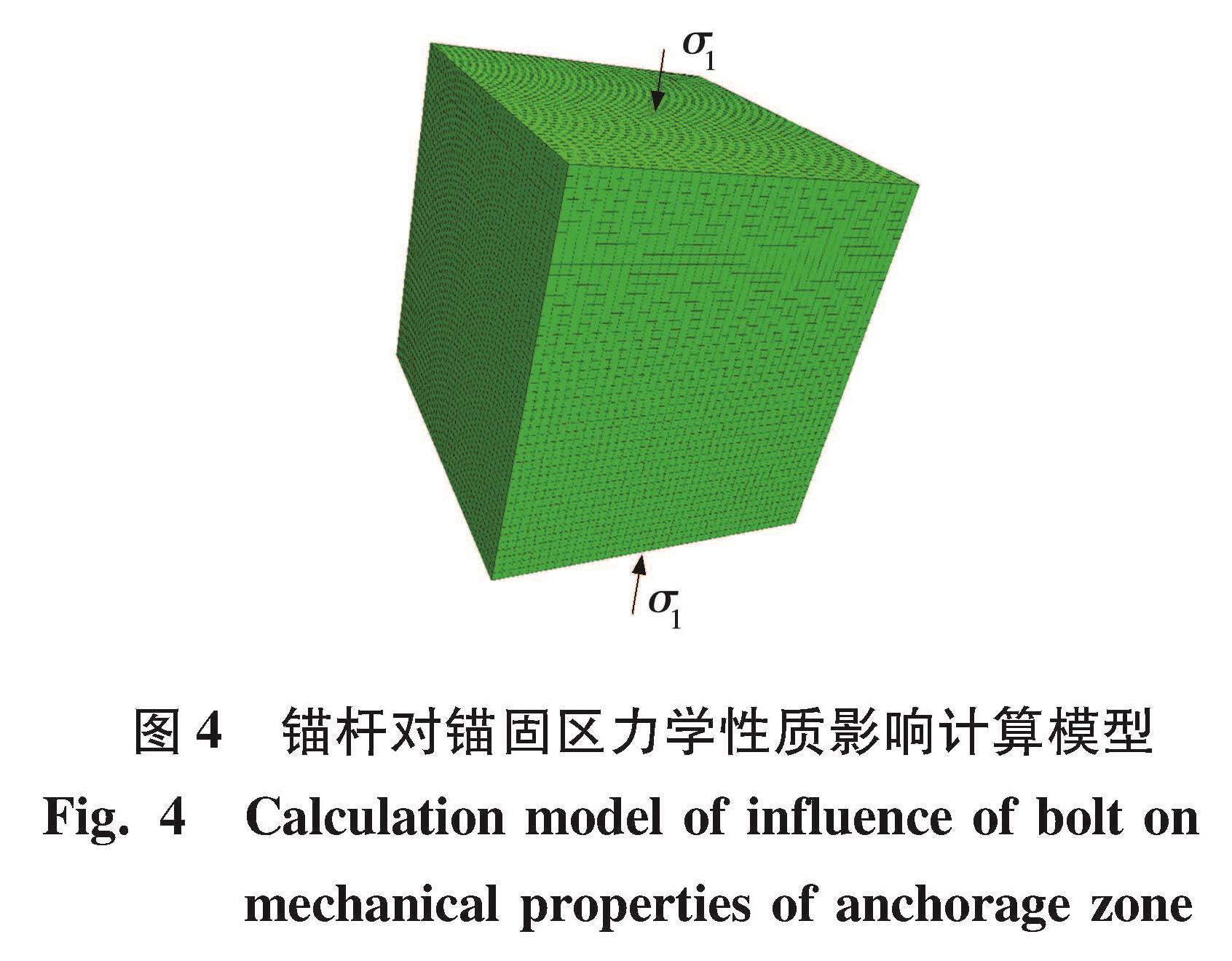
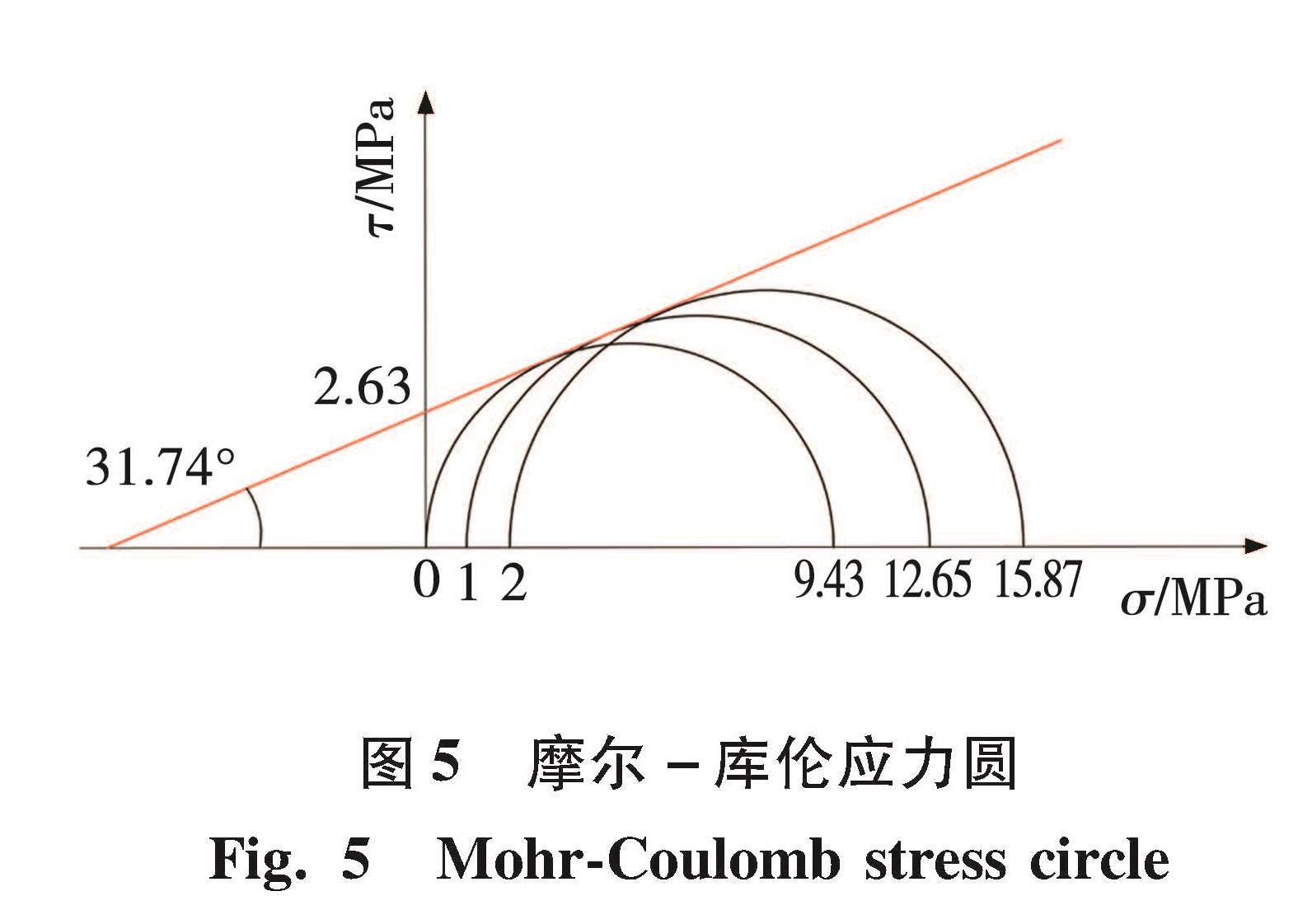
以东荣二矿南二下采区16号煤层的回风下山巷道为原型,研究锚杆支护参数对锚固区围岩体力学性质的影响。应用FLAC3D数值模拟软件,确定模型尺寸为长4.0 m,宽4.5 m,高4.5 m,在数值计算建模中,锚杆采用FLAC3D内置单元体 cable 进行模拟,其力学参数与现场一致,见表2,其中σ为单轴抗压强度,σc为单轴抗拉强度。对试件分别进行单轴压缩、围压1 、2 MPa 3种力学实验,以单轴压缩为例,锚杆对锚固区围岩体力学性质影响计算模型见图4。并得到相应的摩尔-库伦应力包络线见图5。
图4 锚杆对锚固区力学性质影响计算模型
Fig.4 Calculation model of influence of bolt on mechanical properties of anchorage zone
3.1 锚杆间排距对锚固区围岩体力学性质的影响
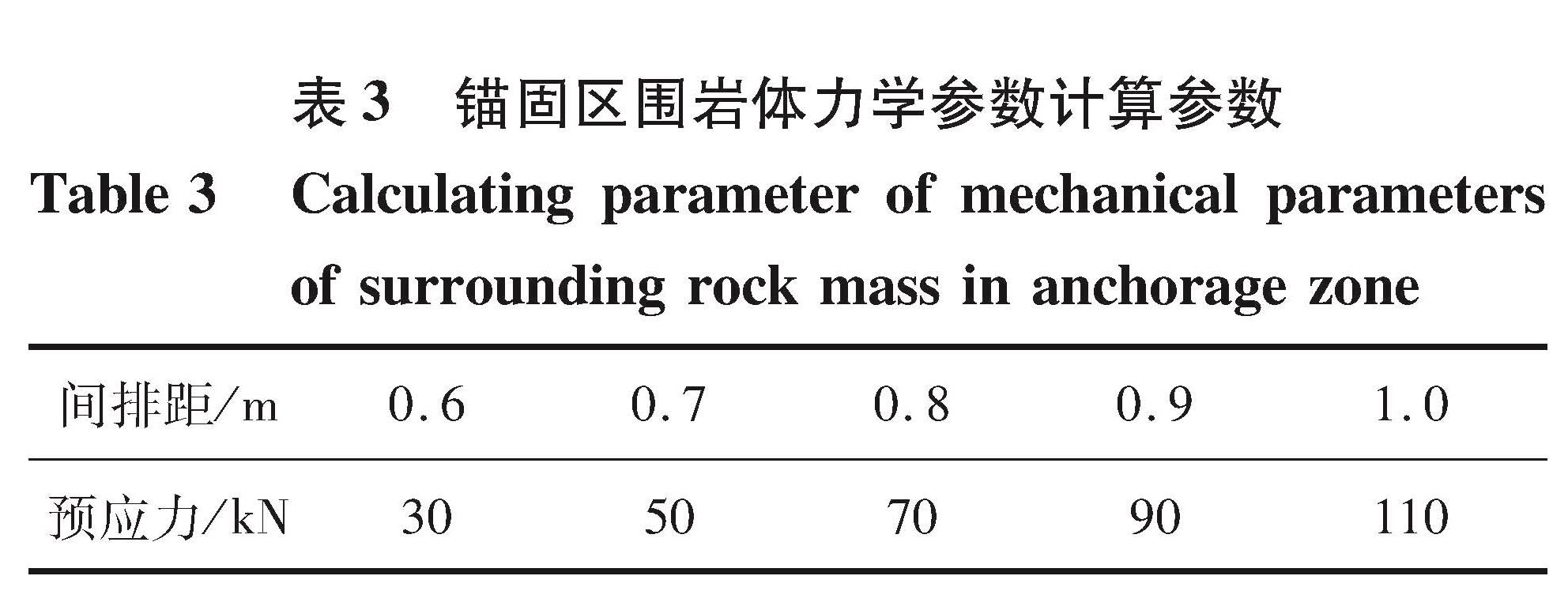
由前述可知,塑性破坏能与锚固区围岩体力学参数有着密切关系,因此讨论锚杆支护参数与锚固区围岩体力学参数的关系,进而研究巷道支护优化方案。所设计锚杆间排距参数见表3。采用控制变量法,间排距为0.6、0.7、0.8、0.9、1.0 m,其余变量:预应力 30 kN,锚杆直径 22 mm,锚杆长度 2.2 m。
表3 锚固区围岩体力学参数计算参数
Table 3 Calculating parameter of mechanical parameters of surrounding rock mass in anchorage zone
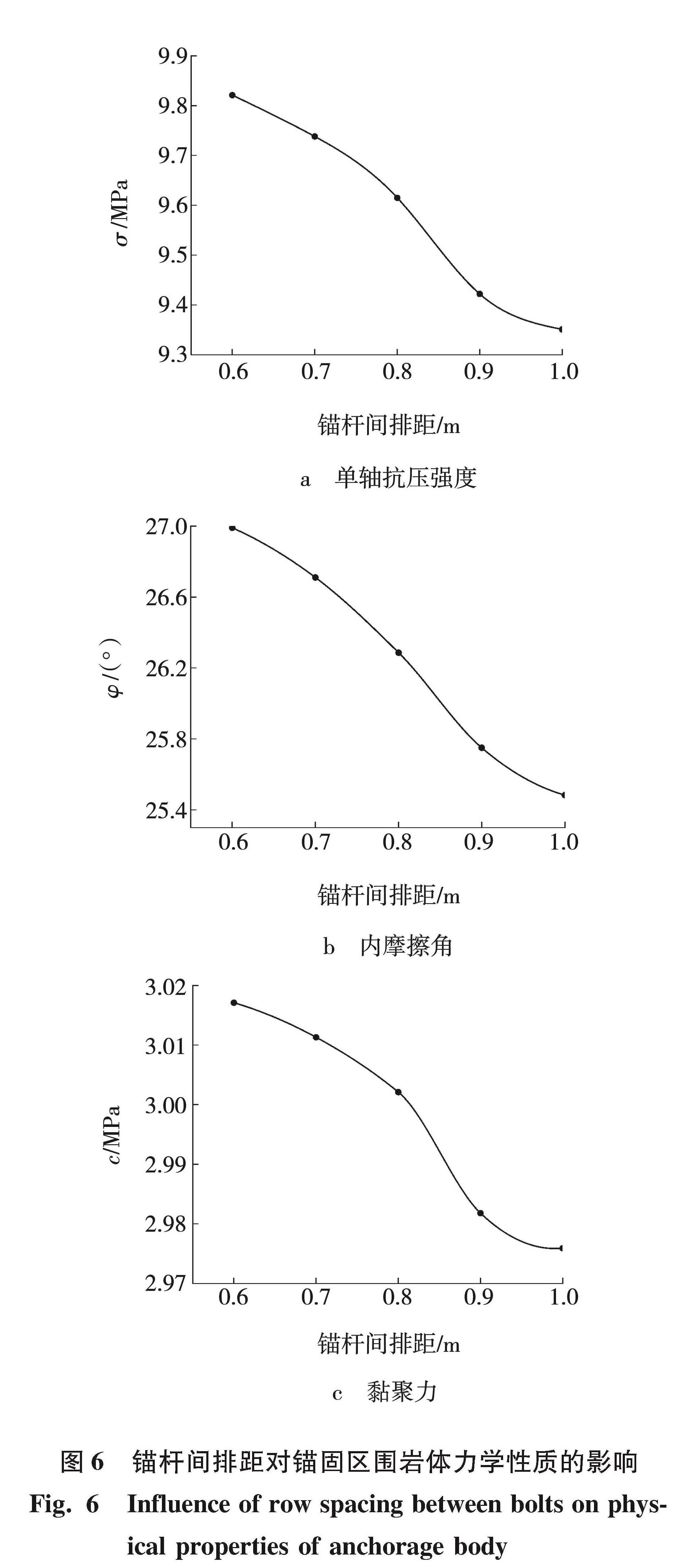
对模型开展重复实验:首先对岩石单轴抗压强度进行测试,之后分别在围压1、2 MPa条件下进行伪三轴抗压强度的实验,采用FLAC3D内嵌的FISH语言编程提取出模型应力应变数据,绘制其应力应变曲线,结合摩尔应力圆的包络线计算得出内摩擦角和内聚力,汇总实验结果,绘制锚杆间排距对锚固区围岩体单轴抗压强度、内聚力及内摩擦角的影响曲线见图6。由图6a可知,随着锚杆间排距的减小,锚固区岩体单轴抗压强度呈递增趋势,间排距由1.0 m到0.6 m时,单轴抗压强度增加了0.47 MPa。锚杆间排距由0.9 m到0.8 m时,锚固区岩体单轴抗压强度增速明显,增幅占比41.1%,此区间曲率最大,锚固区岩体单轴抗压强度随锚杆间排距的减小呈先慢再快后慢的增大趋势。由图6b可知,随着锚杆间排距的减小,锚固区岩体内摩擦角不断增大,间排距由1.0m到0.6m时,内摩擦角增加了1.51°,其中,间排距在0.9 m 到 0.8 m 时曲率最大,增幅占比35.6%,锚固区岩体内摩擦角增速随锚杆间排距减小呈增速平缓的增长趋势。由图6c可知,锚固区岩体黏聚力随间排距减小呈递增趋势,锚杆间排距由1.0 m到0.6 m,黏聚力增加了0.04 Mpa,间排距在 0.9 m 到 0.8 m 之间增幅最大。
图6 锚杆间排距对锚固区围岩体力学性质的影响
Fig.6 Influence of row spacing between bolts on physical properties of anchorage body
综上所述,锚杆间排距对单轴抗压强度σ、内摩擦角φ和黏聚力c的影响均随锚杆间排距的减小而增大,但0.8 m之后增幅减小,各力学参数在 0.9~0.8 m 之间增幅最大。故选择0.8 m间排距作为最优设计间排距。
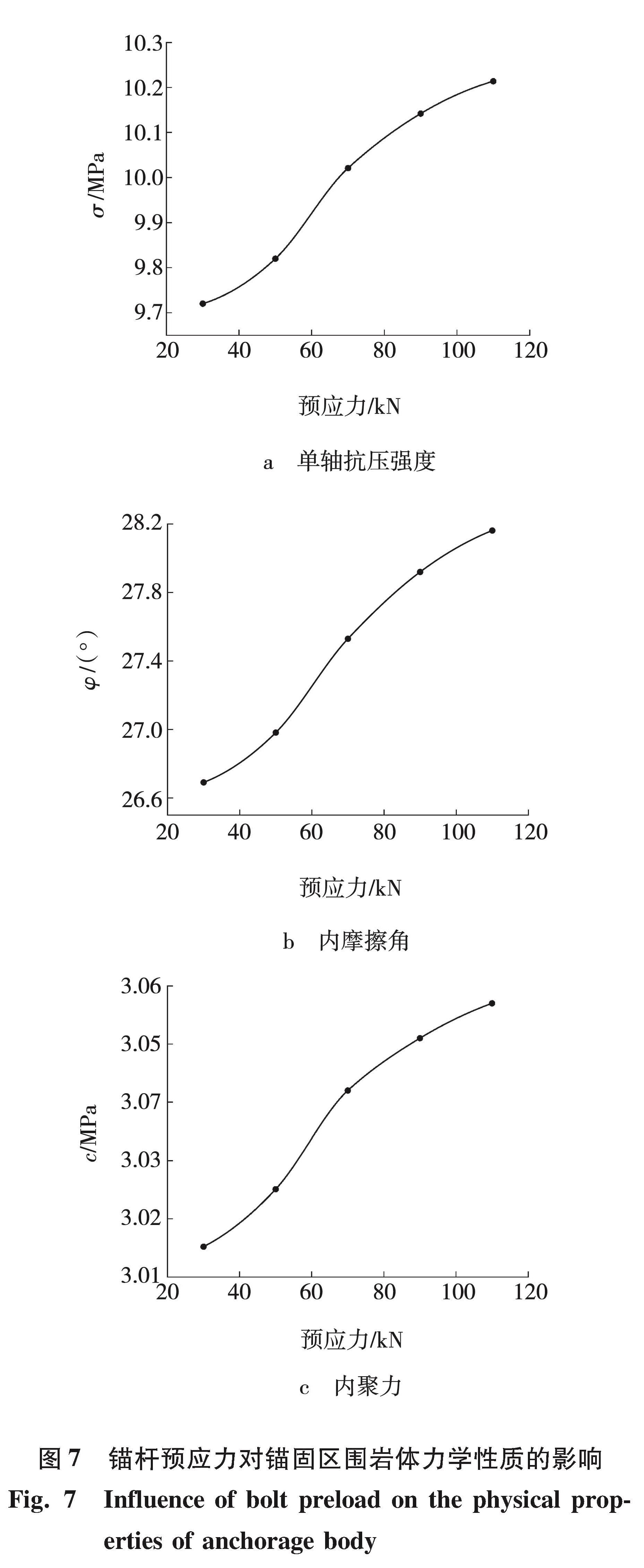
3.2 锚杆预应力对锚固区围岩体力学性质的影响依据表3所设计的实验方案,锚杆预应力设计为 30、50、70、90、110 kN,锚杆间排距取 0.8 m,其余变量均控制为:锚杆直径 22 mm,锚杆长度 2.2 m。实验结果如图7所示。
由图7a可知,随着锚杆预应力的增加,锚固区围岩体单轴抗压强度逐渐增大,预应力由30 kN到110 kN时,单轴抗压强度增加了 0.49 MPa,锚杆预应力从50 kN到70 kN,单轴抗压强度增幅明显,当锚杆预应力达到 70 kN 后,单轴抗压强度增速呈减缓趋势。由图7b可知,锚杆预应力对锚固区围岩体内摩擦角的影响呈递增趋势,预应力由30 kN 到 110 kN 时,内摩擦角增加了1.47°,锚杆预应力从50 kN到70 kN,内摩擦角增幅最大,当锚杆预应力达到70 kN后内摩擦角增速呈减缓趋势。由图7c可知,锚杆预应力对锚固区围岩体黏聚力的影响并不明显,锚杆预应力从30 kN到110 kN 时,黏聚力增加了0.042 MPa,其中,锚杆预应力从50 kN到70 kN时,锚固区围岩体试件黏聚力增幅较大,当锚杆预应力达到70 kN后内聚力增速呈减缓趋势。综上所述,锚固区围岩体单轴抗压强度σ、内摩擦角φ和黏聚力c均随锚杆预应力的增大呈递增趋势,考虑增幅变化情况,选取锚杆设计预应力为70 kN。
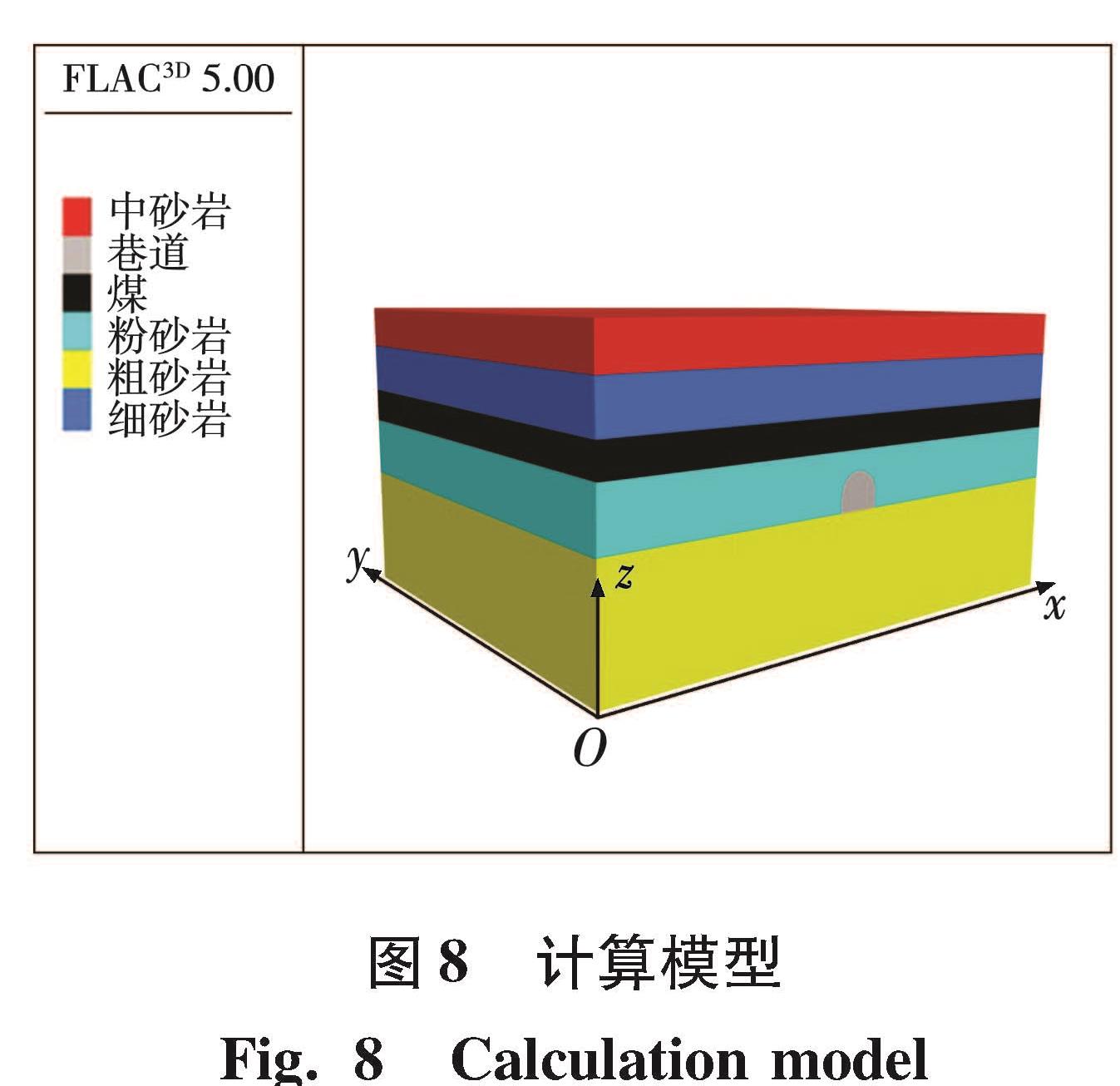
4 数值模拟优化方案4.1 模型的建立为研究深部巷道在支护优化前后的能量、应力状态和变形情况,将模拟巷道设计在砂岩中。该模型以走向方向为y轴,倾向为x轴,重力方向为z轴。沿x、y、z轴方向的长度分别为50、40、50 m。巷道宽4.0 m,高3.8 m。网格划分原则为巷道附近区域密集,远处稀疏。模型共有30 152个节点,26 200个单元,如图8所示。根据实际情况,共建立了4个不同岩性的岩层以及1个煤层,边界条件设置:模型底部边界对水平方向和竖直方向节点速度进行约束,模型侧边界仅对节点水平速度进行约束,模型上边界不施加任何约束,为自由面。煤及顶底板岩层参数与东荣二矿地质参数相同,取值见表3。
4.2 参数的选取
东荣二矿巷道采用直墙半圆拱形断面,巷道宽为4.0 m,高为3.8 m。南二下采区16煤层回风下山巷道现有支护参数中顶部锚杆间、排距为1 000 mm×1 000 mm,采用16 mm×2 200 mm的左旋螺纹钢高强锚杆,3根锚杆垂直顶板打设,锚索采用18.9 mm ×6 300 mm 左旋钢绞线2根,间排距为2 000 mm×800 mm。帮锚杆间、排距为1 000 mm×1 000 mm,2根位于拱脚处,帮部锚杆打设无仰角,两帮锚杆为16 mm×2 200 mm,锚杆使用树脂锚固剂MSK233523 mm×350 mm进行锚固,树脂锚固剂的长度为35 cm。
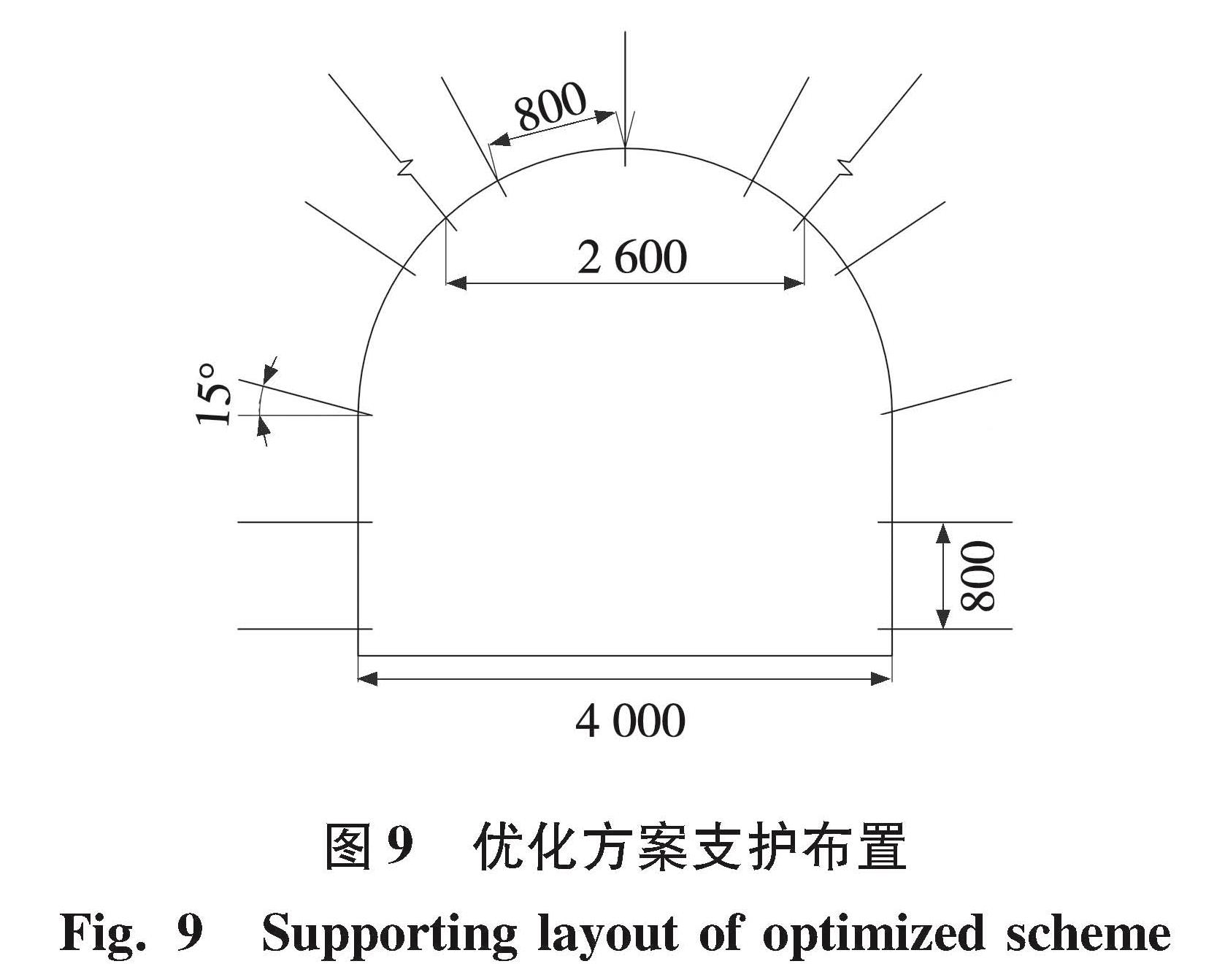
针对上述分析,对原支护方案进行优化,顶板锚杆选择22 mm×2 200 mm长预应力螺纹钢锚杆,预应力为70 kN,间排距由1.0 m×1.0 m优化为0.8 m×0.8 m,锚索保持不变; 帮部锚杆为22 mm×2 200 mm长预应力螺纹钢锚杆,布置拱脚两帮处锚杆打设角度为与水平线呈15°[12]。在经济预算允许范围内,顶板锚杆由3根改为5根,帮部锚杆由2根改为3根。优化方案支护布置见图9。模拟中主要采用库伦-摩尔塑性模型,物理力学参数见表4。
4.3 支护方案对比
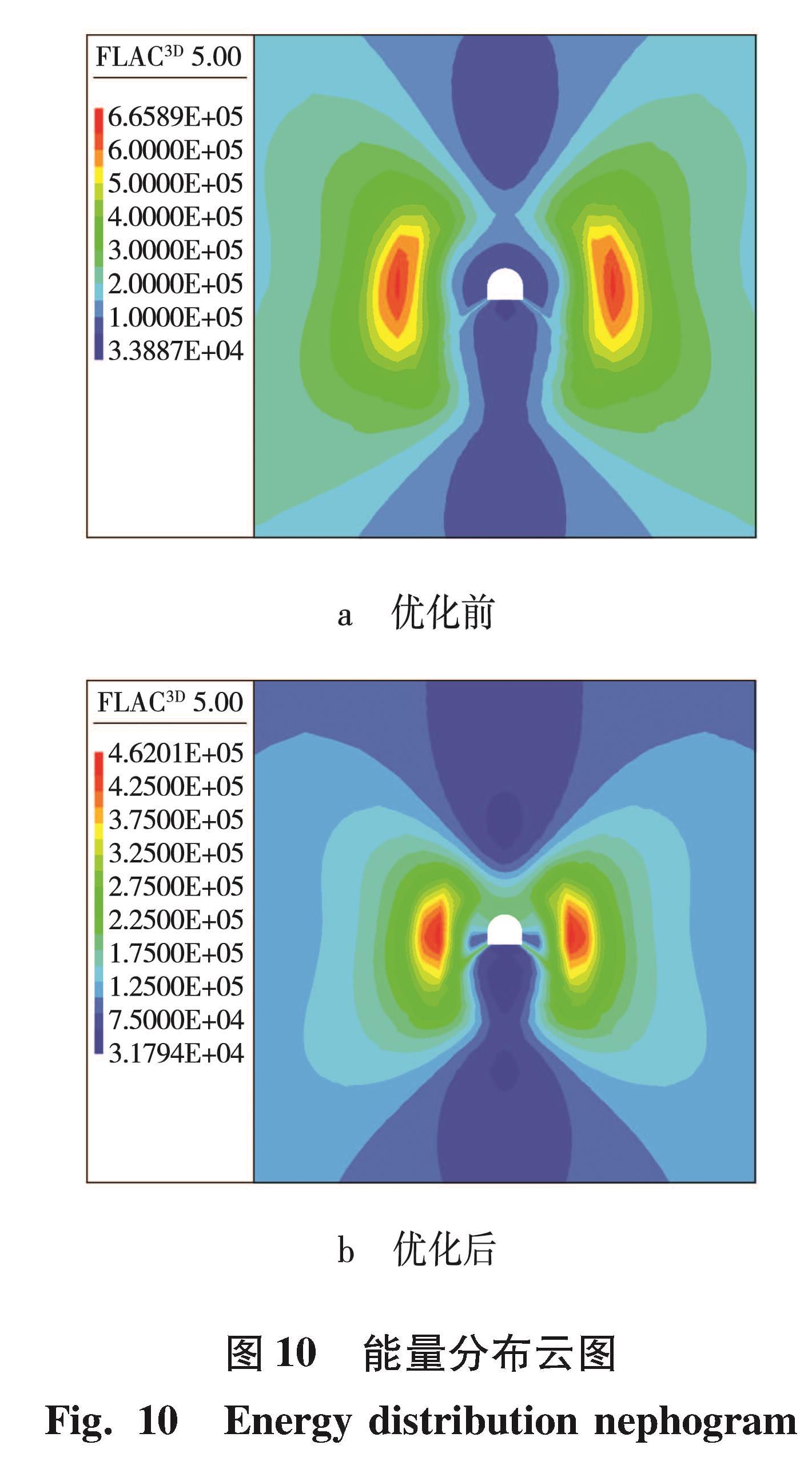
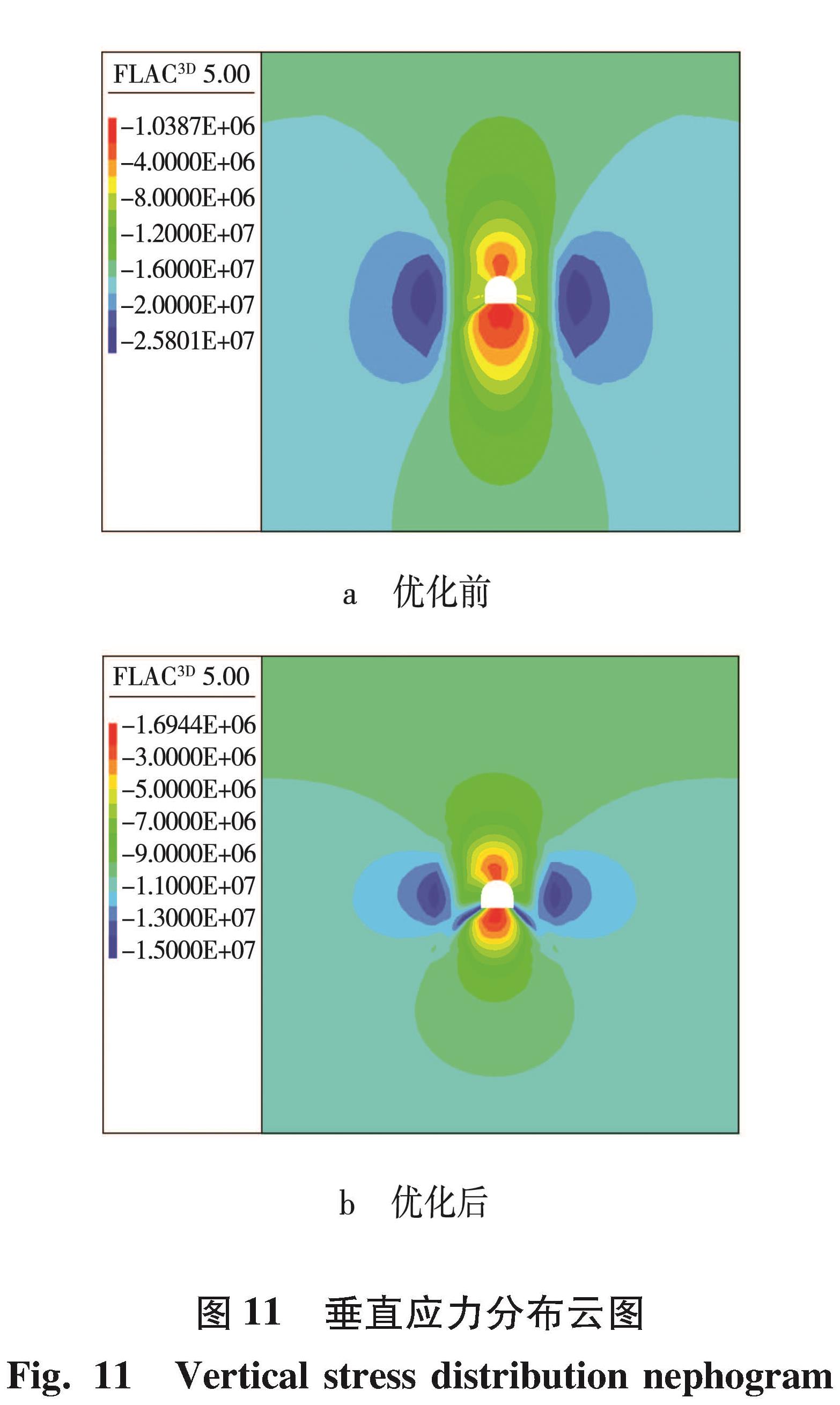
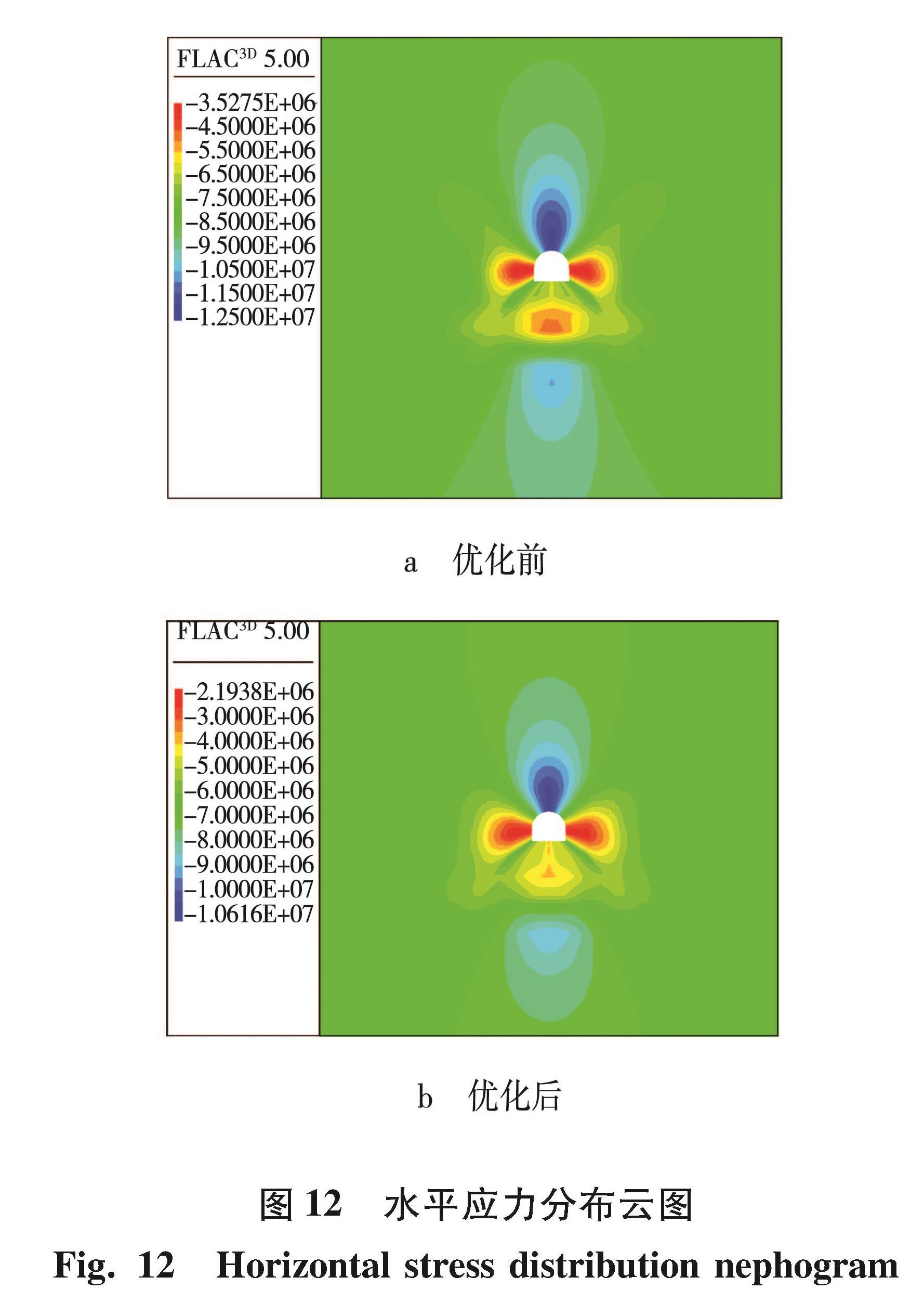
通过数值模拟比较分析优化前后方案的能量分布、应力分布如图 10~12所示。验证优化后支护参数的合理性。
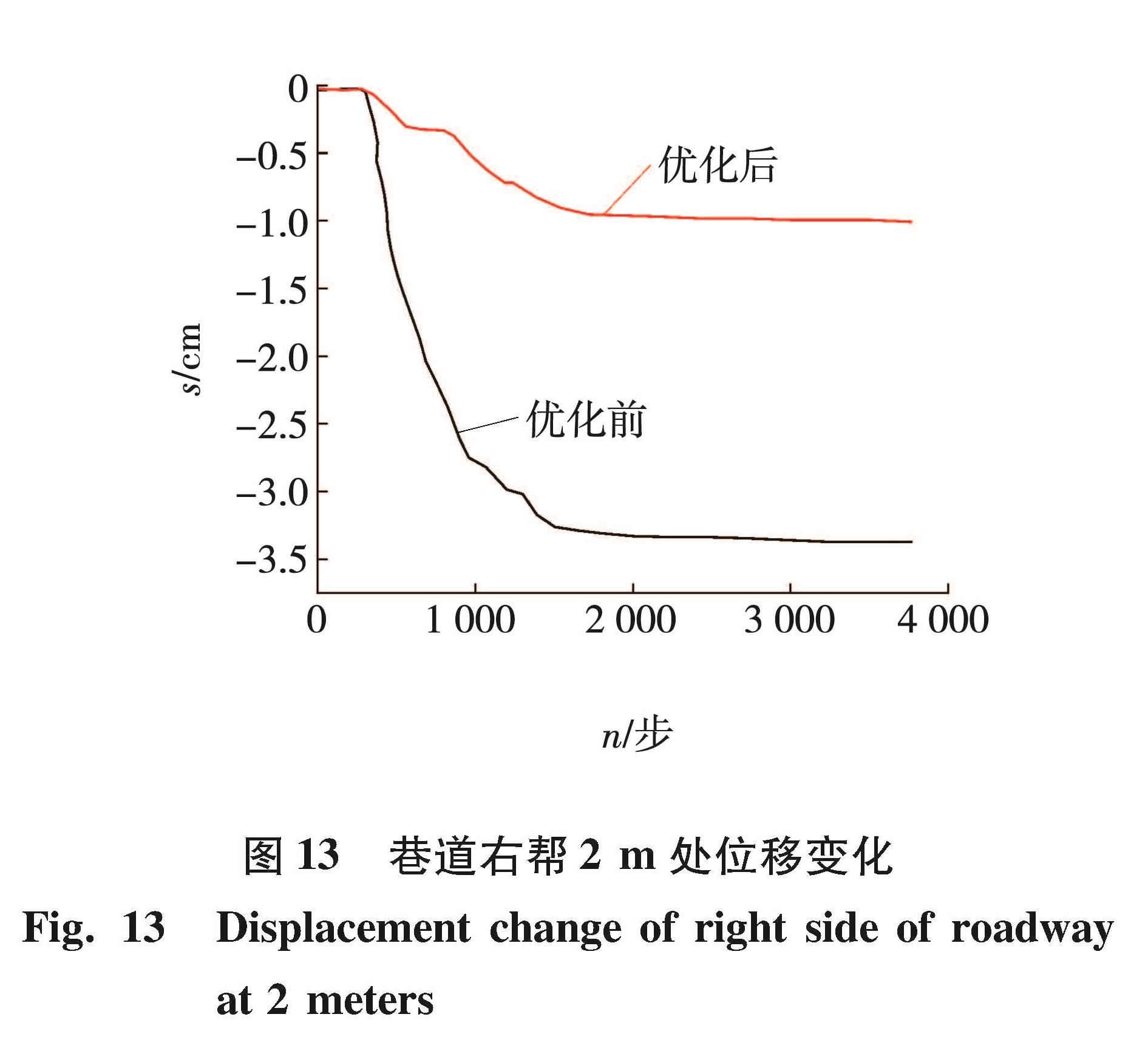
从图 10~12可以看出,巷道在原支护方案下,围岩附近能量积聚大,且能量值较高,特别是在两帮集中,易出现变形,与现场看到的现象一致,经过优化后,两帮能量明显减少,集中程度降低,能量值从665.89 kJ/m3左右减少到了462.01 kJ/m3左右,减少了约30.62%。从垂直应力分布云图中看出,巷道在原支护方案下,两帮受到的垂直应力大,且集中范围大,集中明显,经过优化后,两帮垂直应力集中程度下降,由25.8 MPa下降到15.8 MPa,下降了38.76%。方案优化前后的位移s变化如图 13、14所示。
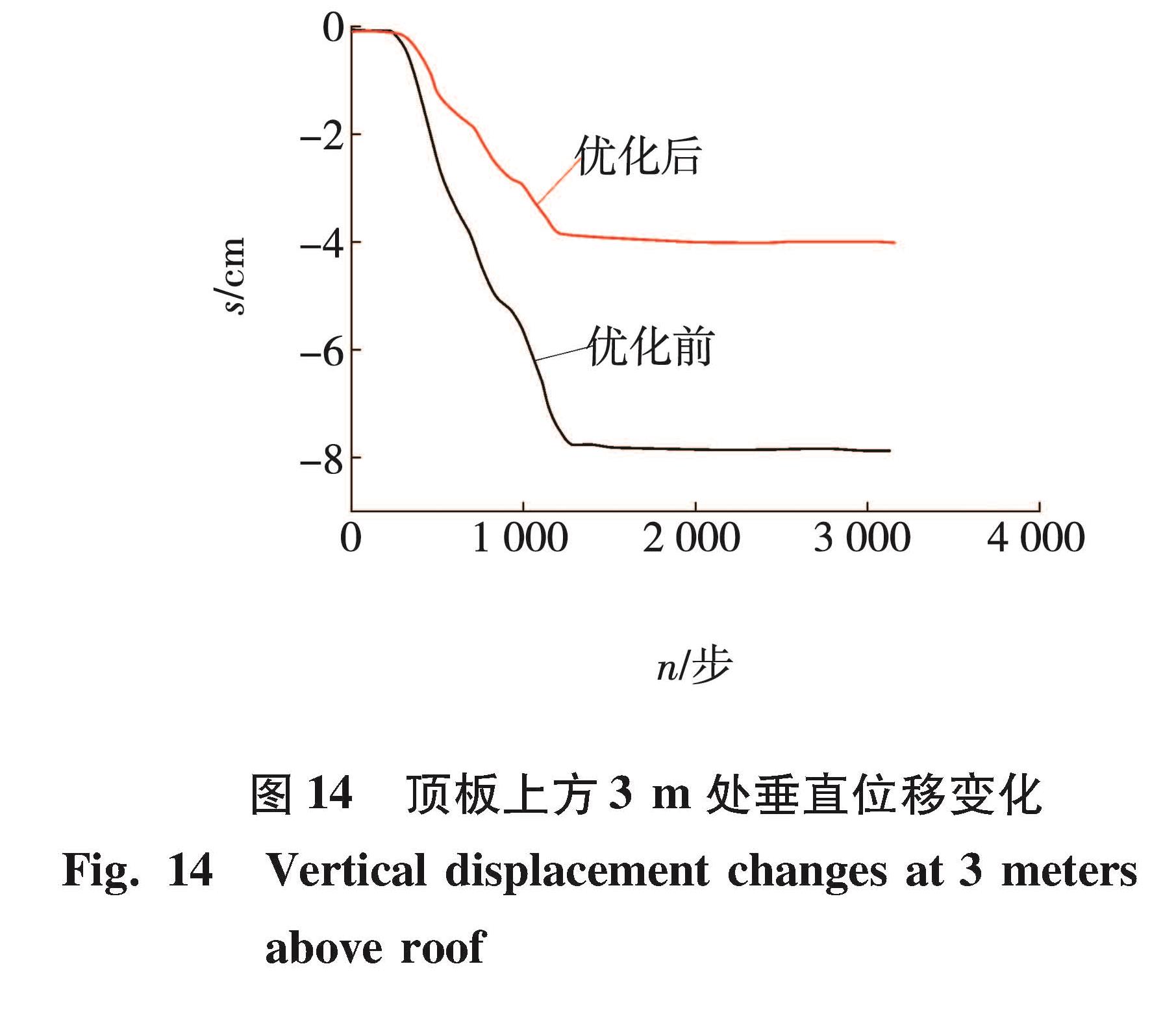
从图 13可以看出,位移量从3.29 cm左右减少到了0.90 cm左右。由此可见,优化后方案很好地控制了两帮的变形。在水平应力分布中,巷道围岩顶底板受水平应力的影响较大,在现场中顶板也出现了变形破碎,进行优化后,应力集中程度减小。从图 14可以看到,顶板位移从7.81 cm左右减少到了3.97 cm左右,减少了49.17%,对顶板的变形破坏进行了很好地控制。
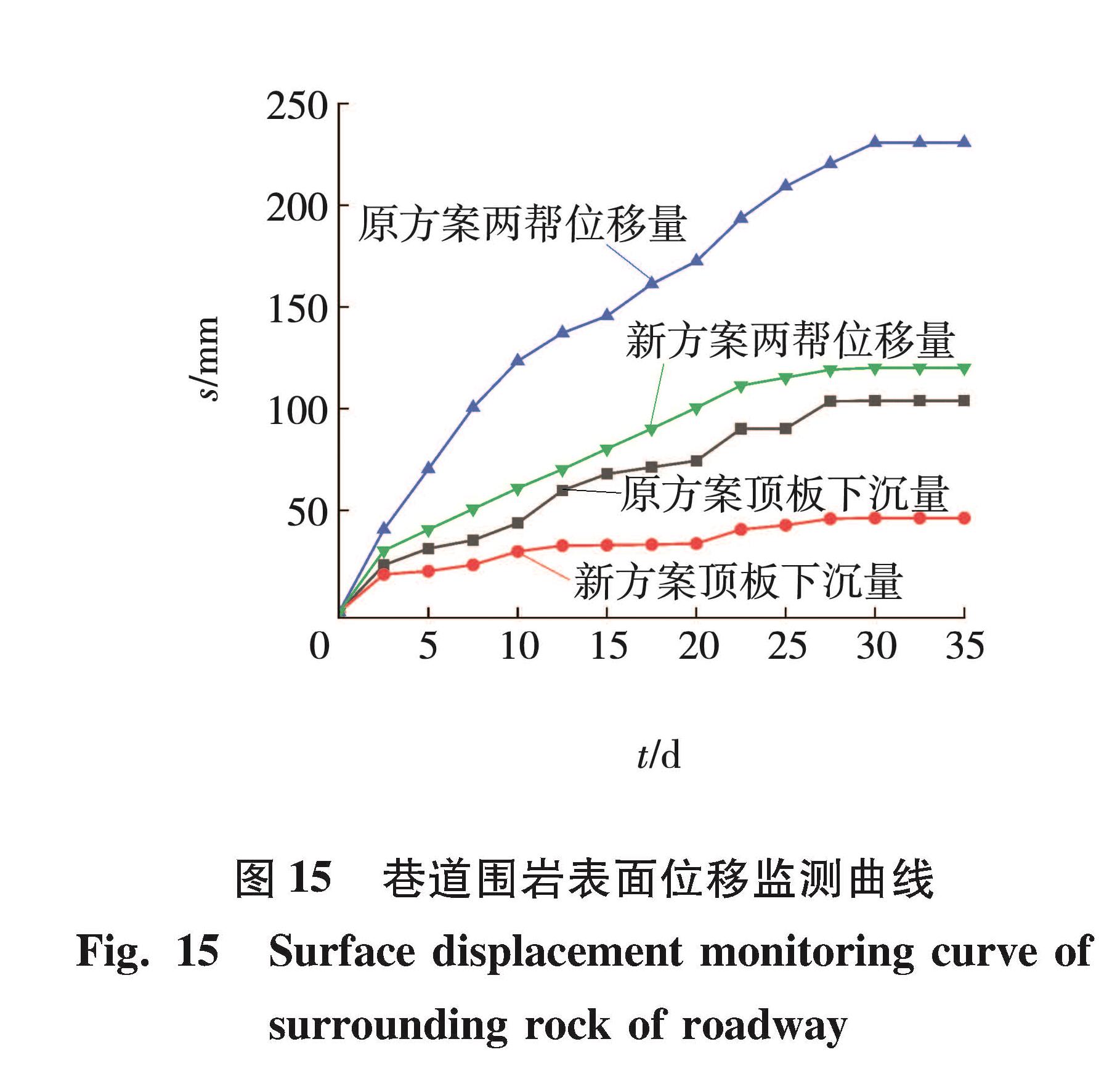
4.4 现场监测回风下山巷道采用合理的支护参数后,在巷道内布置测点,观测频率为2.5 d/次,观测周期为35 d,监测巷道两帮和顶板支护效果,观测数据汇总如图 15所示。由图 15可知,30 d前巷道顶底板和两帮变形量变化较大,30 d后顶板和两帮位移量开始趋于稳定,巷道围岩两帮移近量稳定在120.1 mm,下降了52.17%,顶板下沉量稳定在46.2 mm,下降了51.22%,巷道变形量不大,围岩变形得到有效控制。
综合以上分析,优化后的支护参数,使现场中出现支护不佳的问题得到有效解决,对围岩的稳定性起到了很好的控制作用。
5 结 论(1)黏聚力由1 MPa增加到3 MPa过程中,支护力的大小对塑性破坏能的影响比较明显; 黏聚力在3.5 MPa之后,不同支护力对吸收巷道围岩塑性破坏能的大小基本达到一致,此时不应选取增加支护力的方式来降低巷道围岩内的塑性破坏能。当内摩擦角小于30°时,巷道围岩塑性破坏能受支护力的大小影响明显,此时支护对巷道围岩的变形破坏起到很好的控制作用。
(2)在70 kN预应力下,锚杆在其作用的有效范围内可以更好地吸收巷道围岩塑性破坏能,更好地提高巷道围岩的强度,从而更好地控制巷道围岩的稳定。在0.8 m×0.8 m间排距下,锚杆预应力发挥作用的范围较广,在对锚固区围岩体进行支护后会产生较大的压应力值,压应力区范围也会变大,会使围岩的内摩擦角和黏聚力增大,使塑性破坏能降低,在此间排距下锚杆对围岩的能量吸收作用范围最小。
(3)巷道在支护方案优化后,两帮能量明显减少,集中程度降低,能量值减少了约30.62%。两帮垂直应力集中程度下降,顶板水平应力减小集中程度,两帮移近量和顶板下沉量分别减少了52.17%和51.22%。支护参数经过优化后,使现场中出现支护不佳的问题得到有效解决,对围岩的稳定性起到了很好的控制作用。
- [1] 康红普. 我国煤矿巷道锚杆支护技术发展60年及展望[J]. 中国矿业大学学报, 2016, 45(6): 1071-1081.
- [2] 耿伟乐, 董子文, 郭胜利, 等. 深部高应力巷道变形特性与支护时机[J]. 煤田地质与勘探, 2019, 47(6): 126-134.
- [3] 屠洪盛, 黄昌文, 刘送永, 等. 急倾斜煤层工作面巷道稳定控制机理研究[J]. 煤炭技术, 2020, 39(12): 12-16.
- [4] 薛 飞. 锚杆锚索联合支护机理研究及应用效果[J]. 石化技术, 2020, 27(11): 175-176.
- [5] 孙守孝. 鹿台山煤业巷道支护参数优化研究[J]. 能源与节能, 2020(11): 31-32.
- [6] 侯 兴. 近距离煤层巷道围岩控制技术研究与应用[J]. 江西煤炭科技, 2020(4): 4-7.
- [7] Wang C, Wang Y, Lu S. Deformational behaviour of roadways in soft rocks in underground coal mines and principles for stability control[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(6): 937-946.
- [8] Shan R L, Kong X S, Zhou J J, et al. Study and application of three step supporting design method in coal roadway[J]. Applied Mechanics and Materials, 2013, 353: 252-257.
- [9] 张志强. 掘进巷道围岩稳定性分析及控制研究[J]. 山东煤炭科技, 2016(7): 52-54.
- [10] 穆 磊, 赵龙刚. 基于FLAC~(3D)数值模拟的巷道围岩稳定性及支护参数设计研究[J]. 能源与环保, 2018, 40(12): 170-173.
- [11] 燕晓东. 大倾角煤层采场能量转移特征及其邻近巷道稳定性控制研究[D]. 徐州: 中国矿业大学, 2019.
- [12] 康红普, 姜铁明, 高富强. 预应力锚杆支护参数的设计[J]. 煤炭学报, 2008(7): 721-726.
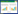 图 1 支护力与塑性破坏能的关系
Fig.1 Relationship of support force and plastic failure energy
图 1 支护力与塑性破坏能的关系
Fig.1 Relationship of support force and plastic failure energy