区域内市级地方政府集中管理调度应急救援力量,煤矿企业与地方政府进行煤矿事故应急救援能力协作建设对煤矿救援效率至关重要。因此,在系统效益最优下实现煤矿事故应急救援能力建设多主体协作,不断提高地方政府与煤矿企业事故应急救援水平具有重要意义。
近年来,在煤矿应急救援领域,已有学者应用灰色模糊综合评价法[1]、熵权法[2]、网络层次分析法[3]、可拓学理论[4]等方法研究煤矿应急救援能力评价。《国务院通知》[5]中指出“将地方煤矿应急救援队伍、设施建设等确认为地方政府财政事权”。地方政府加大对地方煤矿企业的安全投入,有利于双方更加重视煤矿事故应急救援能力协作建设。
目前,国内外学者已对煤矿事故应急能力多主体协作建设进行了深刻研究。周婷婷[6]研究了地方政府与煤矿企业安全生产协作的互惠关系,提出了双方采取一致互惠协作安全防范措施时,地方煤矿企业才愿意加大投入。王金凤[7]等人研究了不同企业在煤矿应急救援的协作演化博弈,提出了在安全生产与监督、应急救援等多方面进行探讨与交流,可加深双方相互监督、相互学习的协作关系。以上文献提出了地方政府和煤矿企业双方的互惠关系分析、煤矿企业间的演化博弈分析,并未对地方政府和煤矿企业的事故应急力量协作建设演化过程有过多分析。演化博弈在其它领域中已经有显著成效,其相关理论在绿色环保[8]、经济领域[9]、环境治理[10]等领域已得到了广泛的应用,而在煤矿应急救援领域研究文献甚少,且主要以企业双方为主体、协同竞争等方面进行的演化博弈研究。在煤炭生产领域,大多学者研究集中于安全投入和监督[11]、安全生产群体行为[12]等方面。由于煤矿应急救援主体行为博弈在应急力量协作建设中是一个有限理性的动态博弈过程,政、企双方会以自身效益最大化为期望进而不断改变策略,最终收敛于一个稳定状态。因此,利用演化博弈构建模型分析地方政府与地方煤矿企业在煤矿事故应急救援力量协作建设的策略选择切实可行。
分析以上结果发现,现有利用演化博弈理论分析地方政府和地方煤矿企业在煤矿事故应急救援能力协作建设的文献尚不多见。笔者借鉴此方法,采用演化博弈理论、MATLAB数字仿真方法来分析协作收益影响参数,在整体效益最优化下,研究相关参数对政、企进行应急救援能力协作建设行为博弈的策略导向的影响,再加以优化关键参数,实现最理想的ESS,促进双方煤矿应急协作能力和能力建设的提高。
1 基本假设负责煤矿事故应急的直接责任人有地方政府和地方煤矿企业[13],双方在事故应急救援前的能力建设程度大小各不相同,差异可能相差悬殊,将双方应急能力建设看作一个系统,则应急能力协作建设是双方选择最优方案的有效途径,使得整体系统达到目标最优。文中设定煤矿事故应急救援能力协作建设博弈主体为地方政府和地方煤矿企业,双方决策理性程度不同,在有限理性条件下进行动态行为博弈。某区域市级地方政府可视为个体参与博弈,地方政府作为地方行政管理部门,接收的信息会更全面,决策理性程度更高,但不是完全理性。地方煤矿企业数量较多,可视为一个群体,接收信息有限,决策理性程度不高。地方政府和地方煤矿企业双方决策均会在煤矿事故应急救援演化博弈中不断学习、模仿,最终趋于稳定。因此假设两者在决策时依据自身的特点所作选择是非理性,信息不对称。
目前,国家在对煤矿事故应急救援的强烈重视下,应急救援能力被纳入地方政府和企业发展规划和总体工作部署,进一步加强领导煤矿安全生产应急管理工作,确定地方政府在其方面的责任,来提高煤矿应急救援能力[14]。根据《国务院通知》,地方政府一定会对煤矿事故应急救援进行投入[5]。地方煤矿企业发生重大事故,地方政府必须进行援助,这是地方政府管辖地方企业和支援的责任。同时地方政府根据中央有关部门条例和自身责任及利益,会对地方煤矿企业进行监督,在应急能力建设方面也会与企业合作。但由于部分地方政府过多考虑到自身利益和对安全建设方面的思想认识不到位,对地方政府采取{严格监督协作,不严格监督协作}策略。地方煤矿企业常以利益为根本,在遵守煤矿安全条例的基础上进行安全投入,为了实现事故整体损失降到最低,减少人员伤亡,地方煤矿企业会积极投入协作。但部分煤矿企业一味注重眼前利益,被利益冲昏头脑,不积极投入,与地方政府在协作建设上难以达成共识,甚至不投入。因此,在地方政府采取策略时,地方煤矿企业会采取{积极投入协作,不积极投入协作}策略。
2 模型的构建选取两个有限理性博弈主体:某区域市级地方政府和地方煤矿企业,地方政府采取{严格监督协作,不严格监督协作}策略,概率分别为x、1-x; 地方煤矿企业采取对应的{积极投入协作,不积极投入协作}策略,概率分别为y、1-y。其中x,y∈[0,1]。主体参数及意义见表1,双方博弈支付矩阵如表2所示。
根据表2的支付矩阵,地方政府采取“严格监督协作”和“不严格监督协作”策略的期望收益函数和平均期望函数分别为
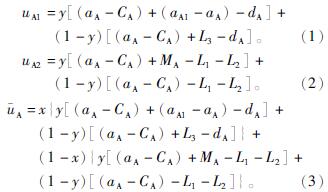
地方煤矿企业在采取“积极投入协作”和“不积极投入协作”策略的期望收益函数和平均期望函数分别为
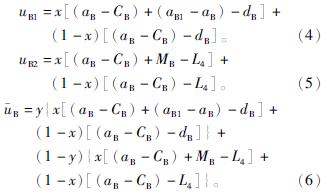
分析地方政府和地方煤矿企业,得出两者复制动态方程为
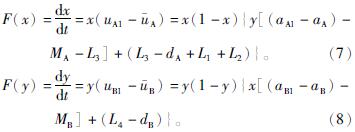
令F(x)=0,F(y)=0,求出均衡点:O(0,0)、A(0,1)、B(1,0)、C(1,1)和D(x*,y*),其中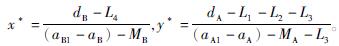
由于考虑到复制动态方程的解不一定是最优解,利用Friedman方法,求出并分析出该系统的雅可比矩阵的局部稳定性,进而求出最优解。将相关参数代入到J矩阵得出:
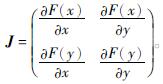
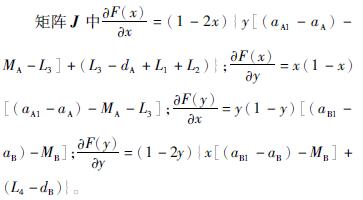
根据公式行列式的值为det J=ad-bc,迹为tr J=a+d,可计算出J矩阵的行列式的值和迹分别为
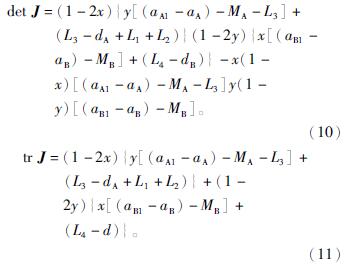
根据Friedman方法,在det J>0且tr J<0时,该均衡点符合最优解。讨论不同情景下,这5个均衡点是否符合上述要求。
3.2 情景讨论情景1:(aA1-aA)-dA>MA-L1-L2且(aB1-aB)-dB>MB-L4时,分别将各个均衡点代入式(10)、(11)中,其局部稳定性如表3所示。表3中A、B为局部不稳定点,D为鞍点(以下情景分析D均为鞍点,不再代入公式计算),O、C为ESS点,系统最终收敛于(0,0)和(1,1)。根据表3画出双方博弈相位图如图1所示。
从图1可以看出,策略演化主要分为区域AOBD和区域ADBC。当双方博弈的策略选择意愿初始点位于区域AOBD时,演化决策路径朝O(0,0)演化,即双方不乐意协作; 当双方博弈的策略选择意愿初始点位于区域ADBC,双方演化决策路径趋于C(1,1),即双方乐意协作。因此,最终双方应急救援的演化结果为协作或不协作。以下情景博弈相位图分析大致类似,不再做具体分析。
情景2:当(aA1-aA)-dA<MA-L1-L2且(aB1-aB)-dB<MB-L4时,A、B点为鞍点,C点为不稳定点,O点为ESS点,系统收敛于点O(0,0)。
情景3:当(aA1-aA)-dA>MA-L1-L2且(aB1-aB)-dB<MB-L4时,A、C点为鞍点,B点为不稳定点,O点为ESS点,系统收敛于点O(0,0)。
情景4:当(aA1-aA)-dA<MA-L1-L2且(aB1-aB)-dB>MB-L4时,A、C点为鞍点,B点为不稳定点,O点为ESS点,系统收敛于点O(0,0)。
三个情景各均衡点分析如表4所示,仅有O点是ESS点,系统最终收敛于点O(0,0),即双方不协作建设。
表4 情景2、3、4时各均衡点的局部稳定性分析
Table 4 Local stability analysis of equilibrium points in scenario 2, 3 and 4
4 数值仿真
为了进一步分析地方政、企业双方的行为博弈决策,提出有利于双方协作建设的有效措施,在此通过MATLAB仿真,赋初值模拟,直观分析双方演化路径、演化趋势,再进行参数优化仿真分析。
4.1 初始参数赋值下的策略演化情景1的理论结果是双方协作,情景2、3、4的理论结果是一方协作或不协作。在国家政策形势下,情景1中的双方协作策略更符合实际,因此假设选定情景1,运用MATLAB软件对复制动态方程相关参数初始赋值,只需在模型构建时,各参数的赋值满足约束条件(L1+L2+L3+L4<dA、dB)及模型分析时情景1的约束条件即可。初始状态下,令x、y初始值为0,循环步长为0.08,双方博弈演化路径如图2a所示。地方政府采取严格监督协作概率分别为0.3、0.5、0.7,代入模型中,观察地方煤矿企业因地方政府策略改变的演化路径,如图2b~d所示。
结合图1可清楚发现图2a区域AOBD面积明显大于区域ADBC,表示双方博弈在初始参数下,向{不严格监督协作,不积极投入协作}的概率比{严格监督协作,积极投入协作}更大。
图2 政、企双方初始状态的策略演变仿真
Fig.2 Simulation of strategy evolution of initial state of government and business
从图2b~d可看出,当地方政府采取严格监督协作的概率为0.3时,部分地方煤矿企业稍有考虑不协作后就坚定选择了与地方政府协作。当概率为0.5时,有了更多地方煤矿企业坚定选择了协作。当概率为0.7时,政、企的协作意愿依然不会改变。
同理,设地方煤矿企业采取积极投入协作的概率分别为0.3、0.5、0.7,代入模型中,如图3所示。
从图3可看出,当地方煤矿企业采取积极投入协作概率为0.3时,仅部分地方政府坚定选择了与地方煤矿企业协作。当概率为0.5时,有了地方政府更加坚定选择了协作。当概率为0.7时,地方煤矿政府几乎坚定选择了与地方煤矿企业协作。
综上可知,x、y的增加都会提高双方的协作几率。由于地方煤矿企业更希望以减少效益损失来进行应急能力建设,其协作意愿较高,因而下文参数设置x为0.6,y为0.7。
4.2 优化参数下的策略演化为了促使政、企策略选择实现帕累托最优,即演化路径向C(1,1)点方向演化,可通过优化鞍点D((dB-L4)/((aB1-aB)-MB),(dA-L1-L2-L3)/((aA1-aA)-MA-L3))中的参数来改变鞍点位置,使更大面积落于鞍点右上方,相关参数有aA、aB、aA1、aB1、MA、MB、L1、L2、L3、L4、dA、dB。利用控制变量法,保证其它影响因子初始值不变,以每组变量来分析影响鞍点D的位置变化。现对相关参数进行分组,组①:协作相对减少的损失量ΔaA=aA1-aA和 ΔaB=aB1-aB组②:侥幸收益MA、MB; 组③:罚金与负效益L1、L2、L3、L4; 组④:先期成本dA、dB。
(1)优化ΔaA=aA1-aA,ΔaB=aB1-aB。当政、企双方止损能力增加时,止损量ΔaA、ΔaB增加,鞍点D向左下方移动,区域ADBC面积增加,演化策略趋向(1,1)的可能性更大,政、企双方的协作意愿也越强。由于设定参数结果归属于情景1,要满足(aA1-aA)-dA>MA-L1-L2且(aB1-aB)-dB>MB-L4条件,此时计算出ΔaA>dA+MA-L1-L2且ΔaB>dB+MB-L4,因此当ΔaA、ΔaB分别增加1个单位,参数优化后双方博弈演化路径如图4所示。
图4 ΔaA、ΔaB优化时的主体策略演化
Fig.4 Evolution of principal strategy during optimization of ΔaA and ΔaB
从图中可以明显看出,ΔaA、ΔaB的增加,其曲线趋势在t∈[0,1]斜率更加陡峭,说明其增加会加快促使政企策略选择趋向于最优,但由于ΔaA由aA、aA1决定,ΔaB由aB、aB1决定,这些参数跟政、企的应急救援能力协作建设有关,双方均要与时俱进,结合新设备、新方法、新理念完善应急预案并加强能力协作建设,以利于提升自身的应急能力建设。
(2)优化MA、MB。当政、企双方因侥幸心理,减少安全投入而额外获得的收益增加时,鞍点D向C点移动,区域ADBC面积减小,演化策略趋向(0,0)的可能性更大,政、企双方存在较大侥幸心理和较高风险决策等均会导致双方不愿意签订协议,不利于应急能力建设。由于设定参数结果归属于情景1,此时计算出MA<ΔaA-dA+L1+L2且MB<ΔaB-dB+L4,因此当MA、MB分别增加3.6、4.4个单位,参数优化后双方博弈演化路径如图5所示。从图5中可以明显看出,MA、MB的增加,曲线斜率为负,演化结果趋向于0,即政、企都扩大了自己的侥幸心理,双方风险提高,会互相传达出危险信号,考虑到自身效益,导致政、企不乐意协作。
图5 MA、MB优化时的主体策略演化
Fig.5 Evolution of principal strategy during optimization of MA and MB
(3)优化L1、L2、L3、L4。当中央有关监管部门给予的惩罚和公众带来的负效益等增加时,鞍点D向O点移动,区域ADBC面积增大,演化策略趋向(1,1)的可能性更大,严厉的处罚、高额的罚金、较大的负效益均会约束双方行为倾向于协作。由于设定参数结果归属于情景1,当L1、L2、L3、L4分别增加0.2个单位,参数优化后双方博弈演化路径如图6所示。从图6中可以看出,提高L1、L2、L3、L4,曲线趋势变陡,说明L1、L2、L3、L4的提高有利于双方合作。但从实践中考虑,适当提高违约金有利于促进并约束政、企向协作发展。
图6 L1、L2、L3、L4优化时的主体策略演化
Fig.6 Evolution of principal strategy during optimization of L1,L2,L3 and L4
(4)优化dA、dB。当政、企双方计划更加深入协作时,协作难度增加,导致协作成本dA、dB增加时,鞍点D向右上方演化,区域ADBC面积减少,演化策略趋向(0,0)的可能性更大,双方为了实现最终效益在各方面进行协作,协作成本增加,会导致双方倾向于不协作。由于设定参数结果归属于情景1,此时计算出dA<ΔaA-MA+L1+L2且dB<ΔaB-MB+L4,因此当dA、dB分别增加3.2、2.8个单位,参数优化后双方博弈演化路径如图7所示。从图中可以分析出,增加dA、dB投入,曲线趋势趋于不协作。双方能快速积极协作是该演化博弈模型所追求的,增加投入才能增进协作的本金,但过多增加协作成本,会导致双方在经济上的负担,也会影响到系统整体的最终演化趋势,需通过增强双方信任度等方法来减少协作成本。
图7 dA、dB优化时的主体策略演化
Fig.7 Evolution of principal strategy during optimization of dA and dB
从图4~7整体可以看出,每组参数相应变化,政、企的行为策略也会相应变化。双方适当提高罚金与负效益L1、L2、L3、L4,会利于系统加快向最优状态演化; 增加侥幸收益MA、MB、协作先期成本dA、dB需要双方考虑自身的经济现状、决策信息是否全面、对方案的风险态度和信任度等来促进双方的合作。
5 结束语由于煤矿事故对社会造成负面影响,据国家政策发布与约束,必须降低不良影响和提高煤矿事故应急救援能力,政、企的协作建设是提高应急能力的有效手段,因此建立了政、企双方协作演化博弈模型。双方考虑自身理性,获得决策结果。以成本效益参数来分析系统协作建设,在我国应急救援领域,政治效益大于经济效益,投入各类成本远大于救援止损。相关成本效益参数优化前后的动态仿真可以直观分析政、企双方行为博弈,为提高煤矿应急救援能力建设出谋划策。研究发现:情景1符合实际所求,在初始条件下,侥幸收益增加,政、企会互相传达风险决策信号,不利于向整体最优演化; 适当提高双方协作的罚金和处罚力度,会促使双方博弈加快向最优状态演化,同时也会削弱政、企双方风险态度; 投入的协作成本与系统趋于最优决策成反比,增加协作投入可以提高应急能力建设,但较高的成本投入会增加经济负担,降低双方协作意愿,在一定程度上,通过增加双方信任度等方法来降低地方煤矿企业在初期的协作投入,达到应急能力建设与协作的最优状态。
通过以上研究,提出两条建议:
(1)适当提高税收比例,建立对官员的责任终身追究制度和声誉机制,并落实事故企业主体责任制度,来加大中央有关监督部门对地方政府不严格监督协作的惩罚力度。加强建设煤矿安全生产诚信制度,推出实施有效的煤炭企业安全生产失信惩罚机制。同时社会公众通过实地调查、网络信息平台、专业协会对地方政府和地方煤矿企业监督,与中央有关监督部门共同约束政、企利益合谋行为和侥幸行为。但监督惩罚力度不易过大,过大容易激发逆反心理,不利于长久协作发展,可以通过提高政策力度、补贴、声誉激励等方法,建立一套全面有效的激励机制。激励与惩罚并用,全面促进整个应急救援能力建设系统的良性循环。
(2)缩短地方政府和地方煤矿企业的协商、信息传递时间,通过增强双方的信任度等手段降低协作成本。地方煤矿企业必须加大培养职工安全生产意识、研发救援技术装备资金和各部门联动应急救援演练等方面建设的投入,并遵纪守法,建立良好信誉。地方政府积极建立完善的创新补偿机制,补偿企业研发投入不足,并主动减少合作流程时间,提高社会福利保障,树立良好的政府形象。政、企双方必须加强政企在应急救援培训中的协作联动性,统一计划管理。政、企多方面多层次相互协调与配合,从而提高双方信任度,减少协作时间成本,有效提高双方协作意愿,增强应急能力建设。
- [1] 黄宏纯. 应急管理科技支撑体系研究[D]. 武汉: 武汉理工大学, 2013.
- [2] 杨 悦, 杨 丹, 陈孝国, 等. 基于梯形Vague集熵权法的煤矿应急救援能力评价研究[J]. 灾害学, 2018, 33(3): 156-160.
- [3] 杨 力, 董一平, 刘程程. 基于网络层次分析法的煤矿应急救援能力评价[J]. 工矿自动化, 2015, 41(3): 114-118.
- [4] 戚宏亮, 宁云才. 基于可拓学理论煤矿安全应急管理能力评价[J]. 煤炭工程, 2016, 48(9): 161-164.
- [5] 国务院办公厅关于印发应急救援领域中央与地方财政事权和支出责任划分改革方案的通知[J]. 湖南安全与防灾, 2020(9): 31-32.
- [6] 周婷婷, 方 乐, 马晓南, 等. 地方政府与煤矿企业安全生产协作的互惠博弈模型[J]. 电子科技大学学报(社科版), 2015, 17(6): 37-43.
- [7] 王金凤, 常禾雨, 翟雪琪, 等. 煤矿应急协作的演化博弈及仿真分析[J]. 矿业安全与环保, 2017, 44(4): 110-114.
- [8] Ashkan H, Reza M. Selection of energy source and evolutionary stable strategies for power plants under financial intervention of government[J]. Journal of Industrial Engineering International, 2017, 13(3): 357-367.
- [9] Andrew R T, Joshua B P, Erol A. Evolutionary games with environmental feedbacks[J]. Nature Communications, 2020, 11(1): 915.
- [10] Dario M, Somnath M, Chiara M, et al. Evolutionary game for task mapping in resource constrained heterogeneous environments[J]. Future Generation Computer Systems, 2020, 108: 762-776.
- [11] Daniel F. On economic applications of evolutionary game theory[J]. Journal of Evolutionary Economics, 1998, 8(1): 15-43.
- [12] 韩 帅, 陈 红, 龙如银. 基于PT-MA理论的煤矿安全群体行为演化博弈分析[J]. 运筹与管理, 2017, 26(11): 77-86.
- [13] 王 一, 王成玉. 2010—2012年因施救不当导致事故损失扩大的原因分析[C]. 北京: 中国煤炭工业安全科学技术学会, 2013.
- [14] 李 英, 米晓红. 基于不完全信息博弈理论的地方煤矿安全监管的博弈分析[J]. 工业安全与环保, 2007(12): 55-56.
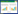 图 1 政、企的博弈相位
Fig.1 Phase game between government and business
图 1 政、企的博弈相位
Fig.1 Phase game between government and business











