地下工程中,硐室开挖会扰动围岩,破坏围岩原有应力平衡,在卸荷状态下围岩蠕变现象十分明显,若控制不当可能会造成大变形、塌方等不良后果[1-2]。研究岩石在卸荷条件下的蠕变特性,对地下工程施工及后期运营具有十分重要的意义[3-4]。
目前,对岩石卸荷蠕变已有较多研究成果,朱杰兵[5]以锦屏二级水电站开挖洞砂岩为研究对象,开展不同卸荷差应力水平下的流变实验,分析其应变特征和蠕变速率。闫子舰[6]开展了大理岩卸围压流变实验,建立一种可描述大理岩卸荷蠕变特性的本构模型。蒋昱州等[7]同时开展了大理岩和绿片岩卸荷蠕变实验,分析岩样卸荷蠕变破坏特征及卸荷蠕变参数与时间之间的变化规律。杨超等[8]基于损伤力学及能量理论,提出一种裂隙岩体卸荷蠕变损伤本构模型。张龙云等[9]开展花岗岩在温度50 ℃下的卸荷蠕变实验,研究蠕变破坏特征及抗剪强度指标的变化规律
以深埋矿井巷道的顶板页岩为研究对象,开展恒轴压卸围压蠕变实验,分析页岩卸荷蠕变过程中的应变特征、蠕变速率和长期强度,基于卸荷蠕变的非线性特征,构建一种新的能较准确描述页岩卸荷蠕变行为的非线性模型,为页岩卸荷蠕变特性及地下工程围岩稳定性研究提供一定参考。
1 实 验试样取自某深埋矿井巷道顶板新鲜页岩,岩层为志留系上统沙帽组,岩块呈紫红色层状,岩样基本物理力学参数:密度24.84 kN/m3,孔隙率0.67%,黏聚力19.78 MPa,内摩擦角38.65°。
根据国际岩石力学学会(ISRM)推荐标准,将岩样加工成50 mm×100 mm的圆柱样,断面打磨平整。采用TLW-2000型岩石三轴流变实验仪,在蠕变实验之前先开展三轴压缩实验,将围压设置为20 MPa,以A-1和A-2岩样进行平行实验确定页岩最大轴向应力为106.46和99.42 MPa,其平均值为102.94 MPa。
2 实验结果与分析2.1 卸荷蠕变初始轴压取页岩三轴实验中最大轴向应力平均值的70%,即72.1 MPa。在恒定轴条件下,围压从20 MPa开始以每一级4 MPa的梯度开始递减直至岩石破坏,每一级围压卸载保持50 h。页岩在恒轴压卸围压应力路径的轴向εz、侧向εc逐级卸载蠕变曲线,如图1所示。
由图1可以看出,页岩在恒轴压卸围压条件下的蠕变特征显著,轴向和侧向蠕变曲线形态较为相似,轴向应变量值总体上大于侧向。岩样在卸载瞬间,首先产生瞬时弹性应变,接着进入衰减和加速蠕变阶段,当达到破坏应力后,岩石发生加速蠕变行为,此时,岩石短暂时间内宏观变形破坏。
2.2 分别卸荷蠕变采用玻尔兹曼线性叠加[10]的方式,将图1处理成分别卸载蠕变曲线,如图2所示。
由图2可知,轴向和侧向的分别卸载蠕变曲线形态相似,两者应变量值差异在1.5倍以内,在第1级卸载下的轴向和侧向瞬时应变皆远大于第2~5级。岩石卸载至第5级之前,轴向应变为2.488×10-2,侧向应变为-1.797×10-2,在破坏围压应力下分别增长为3.481×10-2和-2.549×10-2,增长部分分别占轴向和侧向总应变的28.53%和29.50%。
文献[11]对轴向加载蠕变实验给出式(1)的蠕变速率计算方法,页岩卸载蠕变实验与轴向加载蠕变相处之处在于加载或卸载均是逐级完成,待应变稳定后再进行下一级,故可借鉴文献[11]的蠕变速率计算方法。
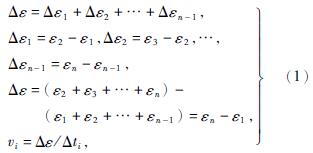
式中:Δti——蠕变时间;
N——蠕变实验数据个数;
vi——应变速率。
由于图2中轴向和侧向的分别卸载蠕变曲线形态相似,仅最后一级卸载才表现有加速蠕变行为,以最后一级卸载等级下的轴向蠕变曲线为例,采用式(1)计算页岩蠕变速率,绘制曲线如图3所示。
由图3可以看出,轴向蠕变速率曲线存在一个初始蠕变速率值为1.302×10-2/h,该速率值在5 h内迅速减小,在稳定蠕变阶段,蠕变速率保持在0.409×10-2/h附近,最后在极短时间内剧增,轴向蠕变速率最大值为2.916×10-2/h。图3轴向蠕变速率曲线可从一定程度上反映岩石的蠕变过程,结合图3和2可以看出,岩石在加速蠕变阶段。蠕变速率和蠕变应变剧增,这是由于岩石蠕变过程中内部微缺陷不断发育,当超过某一临界条件后,微缺陷加速拓展、贯通,由此造成宏观变形破坏。
2.3 长期强度岩石长期强度是岩体工程实践中须引起重视的内容,常用的长期强度求取方法主要有等时偏应力-应变曲线法、稳态蠕变速率与应力关系法及过渡蠕变法[11],其中,等时偏应力–应变曲线法通过取拐点的方式确定长度强度,该曲线还能从某种程度上反映岩石蠕变特征[12],故采用该方法确定长期强度。偏应力为轴向应力与围压之差,择取0 h(趋近于0 h的时刻点)、10、20、30、40和50 h时刻的偏应力-应变数据,绘制等时偏应力-应变曲线如图4所示。
由图4可以看出,等时偏应力-应变曲线具有较为明显的非线性特征,随着时间的增长,曲线逐渐像应变轴靠拢,通过等时偏应力-应变曲线法确定文中页岩长期强度为62.85 MPa,三轴压缩强度为102.94 MPa,前者仅为后者61.05%,这说明岩石在卸载条件下长期强度折减较大。
3 非线性蠕变模型3.1 基础模型Burgers模型是一种应用广泛的蠕变元件模型,其模型结构为H-N-H|N,模型示意见图5。
由图5可以看出,Burgers模型由弹性体、Kelvin体和牛顿体应力串联得到,具有一定的反映岩石弹性、黏弹性性质的能力,但由于Burgers模型中不含塑性元件,无法描述岩石加速蠕变行为,需进行改进。
Burgers蠕变模型的状态方程为
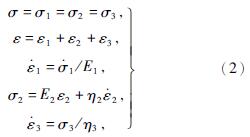
式中:σ1、σ2、σ3——弹性体、Kelvin体和牛顿体的应力;
ε1、ε2、ε3——与σ1、σ2和σ3相对应的应变;
σ、ε——模型总应力及总应变;
E1、E2——弹性体和Kelvin体的弹性模量;
η2、η3 ——Kelvin体和牛顿体的黏滞系数,上标表示对时间的一阶导数。
求解式(2)可得
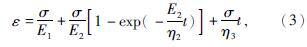
式中,t——时间。
式(3)即为Burgers蠕变模型的本构方程。
3.2 非线性蠕变模型式(2)、(3)的求解过程实质上是解析一个一阶线性常微分齐次方程,式(2)实际上还是线性状态方程,由于岩石卸荷蠕变的非线性特征,黏滞系数在蠕变过程中并不是一个常数,与时间和应力紧密关联,由此,将牛顿体黏滞系数表示为
η3(t)=(η3)/(βt),(4)
式中,β——与应力有关的大于0的参数。
将式(4)代入式(2)可得牛顿体ε3为
ε3=(σ(βt-1))/(η3ln β)。(5)
再综合式(2)、(3)、(5)可得
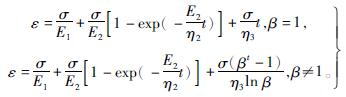 (6)
(6)
式(6)即为在图5模型基础上,考虑非线性的蠕变模型,求导式(6)可得:
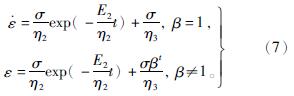
从式(7)可以看出,当β=1时,式(7)退化为传统Burgers模型本构方程,若当t→∞时,此时应变率为常数,可描述岩石长时间蠕变的稳定蠕变阶段; 在式(7)第二式中,当0<β<1时,应变率随t的增大而逐渐减小,可描述衰减蠕变阶段; 当β>1时,应变率随t的增大而急剧增大,可反映岩石加速蠕变阶段。
为反映岩石加速蠕变行为,引入一个含有开关的黏塑性元件见图6。
由图6可见,其本构模型为
ε4=((σ-σs))/(η4)t,(8)
式中:σs——长期强度;
η4——黏塑性元件的黏滞系数。
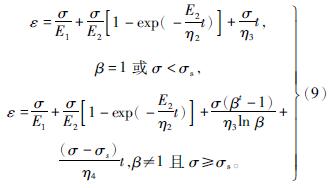
式(9)即为文中改进后非线性蠕变模型的本构方程。
4 参数求解及模型验证文中模型参数有E1、E2、η2、η3、η4、β和σs,其中,E1通过Hooke定律求解即可,σs通过等时偏应力–应变曲线法已确定为62.85 MPa,其余参数求解采用曲线拟合法,通过数学软件1stOpt,基于BFGS算法,拟合图2蠕变曲线,得到模型参数如表1所示,拟合曲线如图7所示。
由图7和表2可以看出,拟合值与实验值吻合较好,尤其是能较准确地拟合页岩加速蠕变曲线,平均R2达到0.988,由此证明文中所建模型的可行性和合理性。传统的Burgers模型为线性模型,无法描述岩石加速蠕变行为,通过将黏滞系数非定常化的方式,建立一个非线性的黏滞系数表达式,由此得到改进后的非线性Burgers模型。改进后模型拟合效果优良,能较好识别岩石加速蠕变,对地下工程围岩时效变形的监测与控制具有重要意义。
5 结 论
(1)页岩在恒轴压卸围压条件下的蠕变特征显著,轴向和侧向蠕变曲线形态较为相似,轴向应变值总体上大于侧向。轴向和侧向的分别卸载蠕变曲线形态相似,两者应变量值差在1.5倍以内。轴向蠕变速率曲线存在一个初始蠕变速率值为1.302×10-2/h,该速率值在较短时间内迅速减小,在稳定蠕变阶段,蠕变速率保持在0.409×10-2/h附近,最后在极短时间内剧增,轴向蠕变速率最大值为2.916×10-2/h。
(2)通过等时偏应力-应变曲线法确定页岩长期强度为62.85 MPa,三轴压缩强度为102.94 MPa,前者仅为后者61.05%,这说明岩石在卸载条件下长期强度折减较大,工程实践中应引起重视。
(3)在Burgers模型的基础上,定义非线性牛顿体,引入黏塑性元件,得到一个新的非线性蠕变模型。拟合对比页岩蠕变实验曲线,平均R2为0.988,证明了文中所建模型的可行性。
- [1] 赵宝云. 岩石拉、压蠕变特性研究及其在地下大空间洞室施工控制中的应用[D]. 重庆: 重庆大学, 2011.
- [2] 许 多, 吴世勇, 张 茹, 等. 锦屏深部大理岩蠕变特性及分数阶蠕变模型[J]. 煤炭学报, 2019, 44(5): 1456-1464.
- [3] Ivaljevi S, Tomanovi Z, Miladinovi B. Creep behaviour of a layered soft rock around the tunnel opening[J]. ce/papers, 2018, 2(2/3): 1057-1062.
- [4] 王 鑫. 深部裂隙岩体卸荷蠕变试验研究及其工程应用[D]. 重庆: 重庆交通大学, 2019.
- [5] 朱杰兵. 高应力下岩石卸荷及其流变特性研究[D]. 武汉: 中国科学院研究生院(武汉岩土力学研究所), 2009.
- [6] 闫子舰. 锦屏大理岩卸荷流变力学特性研究[D]. 上海: 同济大学, 2010.
- [7] 蒋昱州, 朱杰兵, 王瑞红. 软硬互层岩体卸荷蠕变力学特性试验研究[J]. 岩石力学与工程学报, 2012, 31(4): 778-784.
- [8] 杨 超, 黄 达, 黄润秋, 等. 断续双裂隙砂岩三轴卸荷蠕变特性试验及损伤蠕变模型[J]. 煤炭学报, 2016, 41(9): 2203-2211.
- [9] 张龙云, 杨尚阳, 张强勇, 等. 深部花岗岩50℃卸荷蠕变试验研究[J]. 东南大学学报(自然科学版), 2020, 50(2): 91-99.
- [10] 黄海峰. 红层泥岩的损伤和蠕变特性研究[D]. 成都: 成都理工大学, 2018.
- [11] 张春阳, 曹 平, 汪亦显, 等. 自然与饱水状态下深部斜长角闪岩蠕变特性[J]. 中南大学学报(自然科学版), 2013, 44(4): 1587-1595.
- [12] Günther R M, Salzer K, Popp T, et al. Steady-state creep of rock salt: improved approaches for lab determination and modelling[J]. Rock Mechanics and Rock Engineering, 2015, 48(6): 2603-2613.
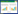 图 1 逐级卸荷蠕变曲线
Fig.1 Creep curves of progressive unloading
图 1 逐级卸荷蠕变曲线
Fig.1 Creep curves of progressive unloading








