强夯法可以有效提高地基的强度与承载力。由于施工设备简单,应用领域广,经济效益好,因此,强夯法在我国得到了广泛的应用。尽管强夯法优点较多,但由强夯施工所引起的振动会对周围既有建筑物产生一定的影响。
目前,关于强夯振动的研究较少,且主要集中在三个方面:一是强夯振动波形的特征分析; 二是强夯振动安全距离的预估研究; 三是减小强夯振动对周围建筑物影响的措施。文献[1-2]通过分析垂直与水平方向速度的衰减规律,得出强夯振动以水平方向的速度为主,分析了强夯振动波形的特点与衰减规律。于海涛[3]根据量纲分析法推导了强夯振动安全距离的预估模型,通过对监测数据的统计分析,验证了计算结果安全可靠。张露露等[4]通过强夯实验的地面振动监测数据,采用非线性回归分析的方法,拟合出强夯振动速度与安全距离的计算公式。左正轩[5]模拟分析了无隔振、空沟隔振以及双道隔振墙三种强夯振动模型,通过曲线拟合了三种模型的安全距离与最大振动速度的关系,发现空沟隔振效果最佳,其次是双道隔振墙,最差是无隔振。文献[6-7]结合实际工程,分析了隔振沟对强夯振动的减震效果。
笔者依托华晨宝马铁西工厂升级项目,通过现场实验田的实验数据,分析回填砂土地基强夯振动的波形特征、振动速度与频率的衰减规律,利用量纲分析法建立强夯振动安全距离的数学计算模型,为砂土地基强夯施工提供理论参考。
1 强夯振动实验华晨宝马铁西工厂升级项目,占地面积约为2.9 km2。为达到项目施工对场地地基土处理的技术标准,选取场地两处建立实验田,通过现场实验与监测数据分析,为整个场区地基处理设计提供依据。
实验田以正方形形状开挖,开挖平面尺寸为25 m×25 m,坑底平面尺寸为20 m×20 m,深度为2.0 m,实验田区域土层分布如图1所示,共建立A区与B区两个实验田。本次强夯工程采用三遍强夯工艺,夯锤重180 kN,夯击能为3 000 kN·m,落距为16.7 m,锤径2.5 m,收锤标准是最后两击平均沉降量不大于5 cm,击数不小于15击。
强夯振动采集设备为TC-4850爆破测振仪[8](STMT08050289),传感器为三维一体式传感器(TT0328153)。测试地点位于A区实验田东侧以及B区实验田东南侧,两实验田分别布置3组测试线,每组测试线布置8个测试点,A区实验田振动测试点距离强夯点分别为10、20、30、40、50、60、70、100 m,B区实验田测试点距离强夯点分别为10、15、20、25、30、50、70、100 m。A区实验田进行了振动波峰值速度[9-10]与振动频率监测[11],B区实验田进行了振动波形图监测、振动波峰值速度以及振动频率监测。数据处理标准按《爆破安全规程》(GB6722—2014)[12]进行。
2 实验结果与分析2.1 波形
B区实验田3组振动波形图变化规律大致相同,文中选取一组距离夯击点10、50、100 m三个位置的振动波形图进行波形分析,分别如图2所示。每个位置的振动波形图分别记录了水平径向振动波、水平切向振动波与垂直方向振动波。根据《爆破安全规程》(GB6722—2014)的规定,质点振动速度取三个方向振动的最大值,对应的振动频率为主振频率。
由图2a可知,此监测点的主振波是红色的水平径向振动波,按照波形图的特点,将波形图划分为两个阶段。第一阶段0~0.43 s,振动波从开始到结束时间短且有明显的峰值,主要是由夯锤夯击地面产生的,这部分峰值是此监测点的峰值速度,其对周围建筑物的影响较大,在t=0.028 s,振动峰值速度为1.61 cm/s、振动频率为7.353 Hz。第二阶段0.43~1.00 s,没有明显的峰值点,主要是由强夯夯击地面后余震所产生的,其特点是混乱无章,对周围建筑物的影响较小,故不做具体分析。
由图2b可知,此监测点主振波也是红色的水平径向振动波。在0~0.63 s,振动波存在的时间短且有明显的峰值,是由夯锤夯击地面产生的,其对周围建筑物的影响较大,在t=0.0 105 s,振动峰值速度为0.41 cm/s,强夯振动频率为14.93 Hz。在0.63~1.93 s,没有明显的峰值点,是由夯击余震所产生的,其对周围建筑物的影响较小。
由图2c可知,此监测点主振波仍是红色的水平径向振动波,0~1.0 s为第一阶段,在t=0.324 0 s,质点的振动速度达到最大值0.421 cm/s,水平径向振动为主导波,主振频率为8.772 Hz。1.0~1.9 s为第二阶段。
综上所述,强夯产生的振动波以水平径向振动波为主,波形图分为两个部分,第一部分是由夯锤夯击地面时产生的振动波,持续时间为0~1.0 s,振动峰值速度与主振频率均发生在该阶段,其对周围建筑物影响较大; 第二部分为夯锤夯击地面后余震产生的振动波,该部分振动波杂乱无章,对周围建筑物影响较小。同时强夯振动波动持续时间在2 s之内,夯锤接触地面时间小于0.3 s。
2.2 振动速度衰减A区强夯振动速度峰值随距夯击点距离的变化曲线[13-15]如图3所示。由图3可知,强夯振动过程中质点组Ⅰ~Ⅲ振动速度峰值随距离的增加基本呈现幂指函数的衰减规律[1-4]。在距离夯击点10~40 m范围内,强夯振动速度峰值随距离的增加而快速由7.45 cm/s衰减到1.01 cm/s; 在距离夯击点40~100 m范围内,强夯振动速度峰值在0.28~1.01 cm/s之间出现微小的波动。
B区强夯振动速度峰值随距夯击点距离的变化曲线如图4所示。由图4可知,强夯振动过程中质点组Ⅳ~Ⅵ振动速度峰值随距离的增加基本呈现幂指函数的衰减规律[14]。在距离夯击点10~30 m范围内,强夯振动速度峰值随距离的增加而快速由1.69 cm/s衰减到0.50 cm/s; 在距离夯击点30~100 m范围内,强夯振动速度峰值在0.3~0.6 cm/s之间出现微小的波动。
由以上分析可知,强夯振动速度峰值随与夯击点距离的增加基本呈现幂指函数的衰减规律,在距离夯击点10~40 m范围内,强夯振动速度峰值随距离的增加而快速减小; 在距离夯击点40~100 m范围内,强夯振动速度峰值作微小的波动。
2.3 振动频率衰减
A区强夯振动主频率随距夯击点距离的变化曲线[16-20]如图5所示。由图5可知,组Ⅰ~Ⅲ强夯振动主频率随距离的增加呈现减小-增大-减小-增大的变化规律,变化幅度大。其中,在距离夯击点10~20 m范围内,强夯振动主频率峰值由17.24 Hz降到11.11 Hz; 在距离夯击点20~40 m范围内,强夯振动主频率峰值由11.11 Hz增加到14.71 Hz; 在距离夯击点40~70 m范围内,振动主频率峰值由14.71 Hz降到10.75 Hz; 距离夯击点70~100 m范围内,强夯振动主频率峰值由10.75 Hz增加到12.57 Hz。
图5 A区强夯振动主频率衰减曲线
Fig.5 attenuation curve of main frequency of dynamic compaction vibration for zone A
B区强夯振动主频率随距夯击点距离的变化曲线如图6所示。由图6可知,组Ⅳ~Ⅵ强夯振动主频率峰值随距离的增加呈现增大-减小-增大-减小的变化规律,变化幅度也较大。其中,在距离夯击点10~20 m范围内,强夯振动主频率峰值由10.02 Hz增加到26.32 Hz; 在距离夯击点20~30 m范围内,强夯振动主频率峰值由26.32 Hz减小到9.80 Hz; 在距离夯击点30~50 m范围内,振动主频率峰值由9.80 Hz增加到16.95 Hz; 在距离夯击点50~100 m范围内,强夯振动主频率峰值由16.95 Hz减小到8.82 Hz。
图6 B区强夯振动主频率衰减曲线
Fig.6 Attenuation curve of main frequency of dynamic compaction vibration for zone B
由以上分析可知,强夯振动主频率峰值受距离的影响较大,且呈现的变化规律也不尽相同。在距离夯击点10~30 m范围内,强夯振动主频率峰值受距离的影响最大; 当距离大于30 m后,距离对强夯振动主频率峰值的影响程度略有减小。
3 强夯振动安全距离预测3.1 量纲分析法的计算模型以强夯振动速度v为因变量,以夯击能W、夯锤质量m、与夯击点距离d、主振频率f为自变量。基于量纲分析法П原理,将这5个物理量中的夯击能W、夯锤质量m、主振频率设定为基本量纲,即可形成2个无量纲П数为
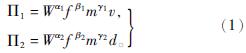
式(1)中的5个物理量可以通过长度L、时间T和质量M来表示,即
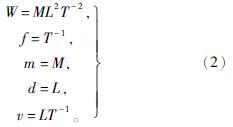
将式(2)代入式(1),得
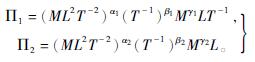
由量纲一致性原理可得
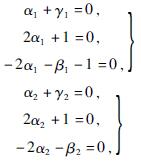
解得α1=1/2,β1=0,γ1=1/2,α2=-1/2,β2=1,γ2=1/2。
将上述参数代入式(1)得
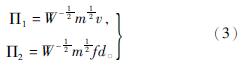
由图3、4分析可知,整个强夯振动过程中速度峰值与距离之间基本呈现幂指函数关系。因此,可构建强夯振动速度与距夯击点距离之间的函数模型为
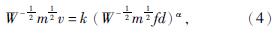
式中:α——衰减指数;
k——当量系数。
为了求解衰减指数α与当量系数k,将式(4)两边同时取对数,得
ln(W-1/2m1/2v)=ln k+αln (W-1/2m1/2fd)。
结合现场实验数据(选取A区与B区各一组数据),令Y=ln(W1/2m1/2v),X=ln(W1/2m1/2fd),通过线性拟合方法拟合直线如图7所示。
由图7可见,图7a为A区的X值与Y值拟合曲线,则可求得A区α=-1.615 06,k=37.16; 图7b为B区的X值与Y拟合曲线,则可求得B区α=-0.476 56,k=0.269 8。
应用式(4)对本工程的强夯振动速度进行预测计算,与实际监测数据进行对比分析,如图8所示。由图8可知,曲线的吻合度较好。A和B区预测值与监测值的误差分析见表1,由表1数据可知,最大误差为21.8%,最小误差为0.28%,平均误差为7.74%; 由表1数据可知,最大误差为27%,最小误差为4.1%,平均误差为12.7%。
3.2 基于非线性曲线拟合的计算模型
由图3、4可知,整个强夯振动过程中速度峰值与距夯击点距离基本呈现幂指函数关系,故可建立强夯振动速度与距夯击点距离之间的函数模型为
v=aebd,(5)
式中:v——振动速度,cm/s;
d——安全距离,m;
a、b——拟合参数。
结合A区与B区现场实验田的监测数据,通过最小二乘法对模型参数进行非线性拟合分析,可求得A区计算模型参数a=10.939 02,b=-0.049 46; B区计算模型参数a=1.541 59,b=-0.022 38。
按式(5)对本工程的强夯振动速度进行预测计算,并与实际监测数据进行对比,如图9所示。由图9可知,曲线的吻合度较差。预测值与监测值的误差分析见表2。由表数据可知,A区预测最大误差为72.2%,最小误差为2.4%,平均误差为24.41%; B区预测最大误差为61%,最小误差为6.8%,平均误差为27.2%。
3.3 模型对比分析
将上述两种强夯振动分析模型的计算结果进行对比可知,量纲法预估模型相较于非线性预估模型,A区最大误差减小50.4%,最小误差减小2.12%,平均误差减小19.46%; B区最大误差减小34%,最小误差减小2.8%,平均误差减小14.50%。
由此可知,基于量纲分析法的强夯振动计算模型的计算精度优于基于非线性曲线法的计算模型。将式(4)变形后即可得到基于量纲分析法的强夯振动安全距离预估计算模型为
d=[vk-1W(α-1)/2f-αm(1-α)/2]-1/α 。
4 结 论通过现场实验田实验,分析了回填砂土地基强夯振动的波形特征、振动速度与频率的衰减规律,基于量纲分析法建立了一种强夯振动安全距离的计算模型。
(1)强夯振动以水平径向波为主导波,波动持续时间在2 s之内,波形分为两个部分,第一部分是由夯锤夯击地面时产生的振动波,持续时间为0~1.0 s,其对周围建筑物影响较大; 第二部分为夯锤夯击地面后余震产生的振动波,对周围建筑物影响较小。
(2)强夯振动速度峰值随与夯击点距离的增加基本呈现幂指函数的衰减规律,在距离夯击点10~40 m范围内,强夯振动速度峰值随距离的增加而快速减小; 在距离夯击点40~100 m范围内,强夯振动速度峰值作微小的波动。
(3)强夯振动主频率峰值受距离的影响较大,且呈现的变化规律也不尽相同。在距离夯击点10~30 m范围内,强夯振动主频率峰值受距离的影响最大; 当距离大于30 m后,距离对强夯振动主频率峰值的影响程度略有减小。
(4)基于量纲分析法建立的强夯振动安全距离计算模型的计算精度较高,两组数据平均误差比基于非线性曲线法模型分别减小19.46%和14.50%。
- [1] 秦伟华, 韩云山, 段 伟, 等. 强夯对填方边坡振动效应分析[J]. 绿色科技, 2015(1): 257-259.
- [2] 张 涛, 吕淑然. 强夯振动波形特征及衰减规律探究[J]. 绿色科技, 2015(1): 259-260.
- [3] 于海涛. 强夯施工振动对建筑物影响安全距离计算方法研究[J]. 建筑监督检测与造价, 2016, 9(1): 28-32.
- [4] 张露露, 方 勇. 强夯振动监测及安全距离预估[J]. 施工技术, 2016, 45(13): 75-77.
- [5] 左正轩. 强夯试验研究及高聚物隔振分析[D]. 广州: 广州大学, 2020.
- [6] 张海江. 强夯振动影响测试[J]. 勘察科学技术, 2017(S1): 183-186.
- [7] 秦伟华, 韩云山, 段 伟, 等. 强夯对填方边坡振动效应分析[J]. 绿色科技, 2015(1): 257-259.
- [8] 林世雄. 爆破安全评估的新设备——TC-4850爆破测振仪[J]. 爆破, 2008(2): 33-52.
- [9] 李云生. 强夯振动安全监测应用探讨[J]. 工程建设, 2020, 52(10): 72-78.
- [10] 黄 璇, 许彩琦. 水库工程坝基强夯振动监测与分析[J]. 水利与建筑工程学报, 2019, 17(6): 236-239.
- [11] 邵安阳, 孙进忠, 肖庭庭, 等. 强夯振动对环境影响的监测与评价[C]//中国地球物理学会. 2014年中国地球科学联合学术年会——专题23: 环境与工程地球物理研究进展论文集, 2014.
- [12] 中华人民共和国国家标准编写组. GB 6722—2014, 爆破安全规程[S]. 北京: 中国标准出版社, 2015.
- [13] 阿拉塔, 谭晓晶, 许国山. 场平工程强夯加固振动测试与分析[J]. 低温建筑技术, 2020, 42(8): 89-94.
- [14] 王斯海, 陈海军, 王世坚. 不同土层结构场地强夯振动效应研究[J]. 施工技术, 2016, 45(S1): 15-19.
- [15] 王志楠, 何小飞, 沈锦儒. 强夯地面振动衰减规律探讨[J]. 工业建筑杂志社, 2016(S2): 473-477.
- [16] 王百升. 高能级强夯作用下黄土边坡动力响应规律研究[D]. 西安: 长安大学, 2018.
- [17] 王文强. 桥头桩基在强夯振动波作用下的动力响应分析[D]. 济南: 济南大学, 2017.
- [18] 张力闻. 强夯振动对挡土墙稳定性的影响研究[D]. 北京: 中国地质大学(北京), 2017.
- [19] 张宏伟. 阶梯型土坡平台强夯施工振动效应及振害防治研究[D]. 重庆: 重庆交通大学, 2016.
- [20] 张忠和. 强夯法加固地基振动效应数值分析[D]. 北京: 中国地质大学(北京), 2015.
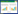 图 1 实验区土层分布
Fig.1 Soil layer distribution in experimental area
图 1 实验区土层分布
Fig.1 Soil layer distribution in experimental area











