自2003年,Bruneau 等[1]首次提出“可恢复功能抗震结构”的概念以来,具有恢复功能的防震结构已成世界地震工程领域的研究热点。自复位摩擦耗能支撑(Self-centering energy dissipation braces, SCED)是一种典型的具有可恢复功能结构,具有良好的变形能力、能量耗散能力及恢复能力[2]。近年来,研究者们陆续采用了一系列滞回模型描述自复位摩擦耗能支撑的力学性能。2011年,Ma等[3]使用Bouc-Wen模型[4-5]研究自复位阻尼器响应,该模型可以合理地描述支撑力-位移滞回特性。文献[6-7]基于预压弹簧自复位耗能支撑工作原理和原Bouc-Wen 模型,提出了分段简化恢复力模型,实验验证该模型能准确描述各阶段的滞回响应。2016年,Zhou等[8]在流变学模型的基础上,提出了一个预测自复位屈曲约束支撑滞回行为的弹塑性模型。樊晓伟等[9]提出了由双Bouc-Wen 模型和一组线弹性模型组成的支撑非线性原理模型,通过模拟确定了模型参数。2020年,Zhang等[10]提出了经改进的旗形模型(Modified flag-shaped model,MFS),MFS模型包括线性部分、双线性部分和具有滑移区的弹塑性部分,可以更有效反应自复位摩擦耗能支撑的滞回响应特性。
为了能够准确给出模型参数影响规律,确定模型参数取值,笔者分析MFS模型参数的敏感性,给出模型参数合理取值范围,采用CKF算法识别MFS模型在线参数,验证该算法模型参数识别精度与计算效率。
1 自复位摩擦耗能支撑系统1.1 SCED支撑滞回模型SCED支撑作为一种耗能构件,具有良好的耗能效果和结构残余位移控制等优点。其中,MFS模型可以准确描述SCED支撑滞回特性,MFS模型滞回曲线与SCED支撑滞回曲线吻合程度较高,更接近SCED支撑的滞回现象,有效扩展耗能构件在抗震领域的应用。以MFS[10]模型为研究对象,MFS模型由线性部分、双线性弹性部分、具有可滑移弹塑性部分组成,自复位摩擦耗能支撑机理如图1所示。初始阶段刚度K为模型线性、双线性、具有可滑移弹塑性三部分的刚度之和,即K=K1+K2+K3。当摩擦装置启动后,支撑刚度减小至预应力筋刚度K1,卸载初始阶段的卸载刚度等于K1+K3,当力到达激活点b时,刚度变成K1+K2。
MFS的恢复力可表达为
F=K1x+K2R(x)+K3z,
式中,R(x)——双线性弹性模型恢复力,kN。
R(x)具体表达式为
R(x)=x[1-H(x-b)-H(-x-b)]+b[H(x-b)-H(x-b)],(1)
式中:H(x)——海维赛德阶跃函数;
B——激活位移,mm;
z——模型滞回位移,mm。
z微分表达式为
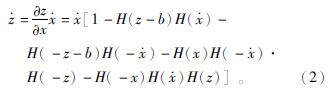
K1、K2、K3由式(3)~(5)给出
K1=AK,(3)
K2=(1-A)(1-Q)K,(4)
K3=(1-A)QK,(5)
式中:A——激活刚度比,A=(1-Q)b;
Q——耗能率,是能量耗散的重要指标,Q=K3/(K2+K3)。
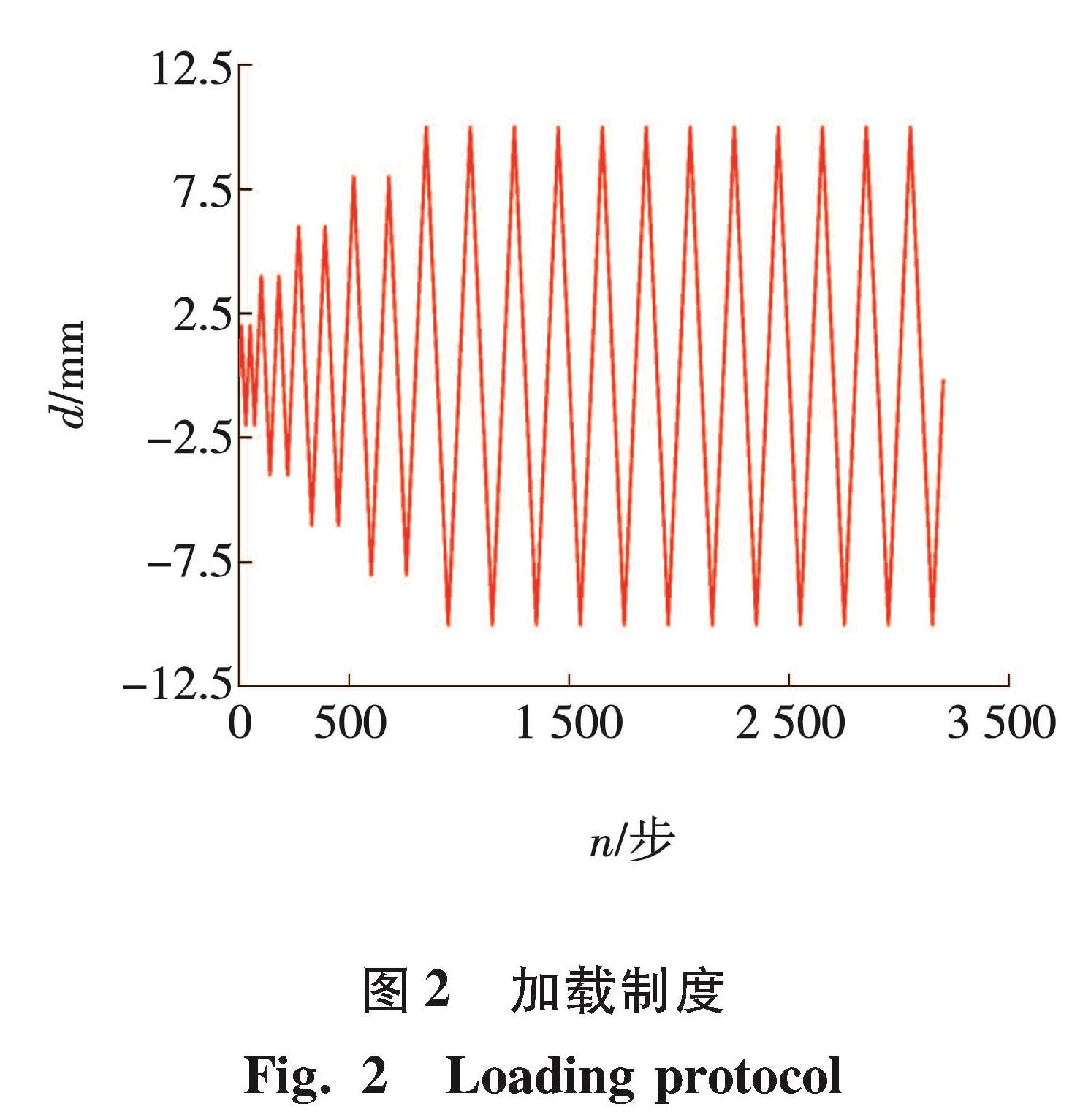
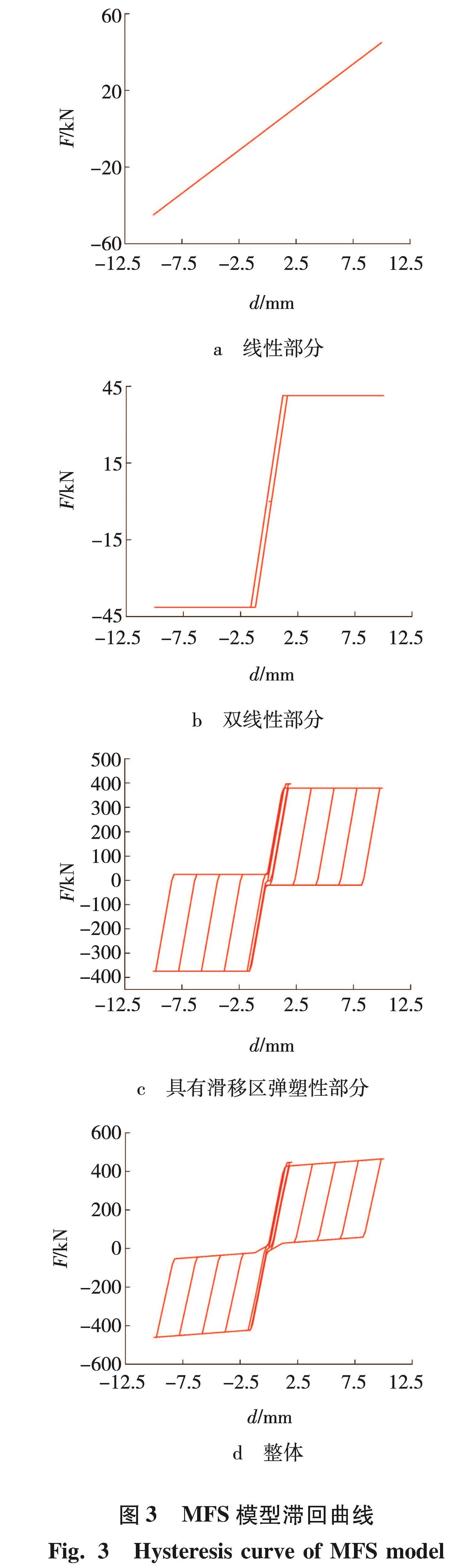
1.2 MFS模型有效性验证为验证本文模拟MFS模型有效性,对MFS模型采用低周期往复位移加载,加载峰值为10 mm,加载步数为3 200步,模型加载制度如图2所示。MFS模型真实参数依次设置为:激活刚度比A=0.015、耗能率Q=0.9、激活位移b=1.4 mm、初始刚度K=300 kN/mm。MFS模型的滞回位移利用四阶Runge-Kutta积分算法得出,计算步长为0.01 s。模拟MFS模型线性部分、双折线部分、具有滑移区弹塑性部分及整体部分模拟结果如图3所示。
由图3可以看出,通过对MFS模型进行低周期往复位移加载,MFS模型线性部分为一条斜直线、模型双线性部分为双折线、模型具有滑移区弹塑性部分及模型整体滞回曲线可以产生一个旗形滞回曲线,得出的计算结果可以反映MFS模型滞回特点,验证了所模拟MFS模型的有效性。
2 MFS参数敏感性分析
在验证MFS模型的有效性的基础上,分别选取MFS模型参数激活点b、初始刚度K、模型耗能率Q、模型激活后刚度比A四个参数作为分析对象,以1.2节参数值作为参数基值,通过MFS模型低周期往复加载分别对四个参数分别进行敏感性分析,分析结构如图4~7所示。给出四个参数在定量处理后的变化规律,从而得到参数取值范围。
由图4可见,以b=1.4 mm为基值,单一调整参数b值大小,b的取值范围为0~3.5 mm,分别研究MFS模型线性部分、双线性部分、具有滑移区弹塑性部分、整体部分恢复力随b值变化规律。
由图4可以看出,随着激活点b值的增加,MFS模型线性部分没有影响,MFS模型双线性部分、MFS模型具有滑移区弹塑性部分、MFS模型整体的轴向恢复力不断增大; 随着支撑轴向力的增大,支撑整体滞回耗能不断增加。
图7 通过对A定量分析模型各部分及整体滞回曲线
Fig.7 Quantitative analysis of each part and the overall hysteretic curve of A
随着激活点b值的增大,MFS模型具有滑移区弹塑性部分,激活位移、激活力逐渐增大,当b=0时,整体滞回曲线近似为线性,耗能几乎为0,当b=3.5 mm时,推迟了模型进入耗能阶段,导致滞回环与真实滞回环卸载路径产生明显差异。因此,建议b的取值范围为0<b<3.5 mm。
由图5可以看出,针对K进行敏感性分析。以K=300 kN/mm为基值,单一调整参数K值大小,K的取值范围为0~750 kN/mm,分别研究MFS模型线性部分、双线性部分、具有滑移区弹塑性部分、整体部分恢复力随K值变化规律。
随着初始刚度K值的增加,MFS模型线性部分的图像斜率增大,MFS模型双线性部分、MFS模型具有滑移区弹塑性部分、MFS模型整体的轴向恢复力不断增大; 初始刚度K与MFS模型轴向力存在正相关关系。因此,建议K的取值范围为K>0。
由图6可以看出,以Q=0.9为基值,单一调整参数Q值大小,Q的取值范围为0~1,分别研究MFS模型线性部分、双线性部分、具有滑移区弹塑性部分、整体部分恢复力随Q值变化规律
随着耗能率Q值的增加,MFS模型线性部分没有影响,MFS模型双线性部分、具有滑移区弹塑性部分、整体的轴向恢复力不断增大; 当Q增加至1时,滞回曲线出现在二、四象限,模型没有意义。因此,建议Q的取值范围为0<Q<1。
由图7可以看出,以A=0.015为基值,单一调整参数A值大小,A的取值范围为0~1,分别研究MFS模型线性部分、双线性部分、具有滑移区弹塑性部分、整体部分恢复力随A值变化规律。
随着激活点A值的增加,MFS模型线性部分的图像斜率增加,MFS模型双线性部分、具有滑移区弹塑性部分、整体的轴向恢复力不断增大; MFS模型双线性部分、具有滑移区弹塑性部分、整体的轴向力会随着耗能率A值的增加而增加,当A增加至1时,滞回曲线变成一条直线,A>1时,模型没有意义。因此,建议A值取值范围为0<A<1。
3 CKF参数识别3.1 CKF识别更新MFS模型参数为了检验CKF识别MFS模型参数的鲁棒性。采用CKF[11]对MFS模型进行在线参数识别,利用低周期往复位移加载,加载制度同1.2节图2。文中设定MFS模型真实参数分别为:激活刚度比A=0.01、耗能率Q=0.9、激活位移b=1.4 mm、初始刚度K=300 kN/mm。激活点b的取值,决定支撑是否快速进入耗能状态。文中选取模型重要参数b作为待识别参数,设定初始参数激活位移预估值b^=2 mm。CKF设别模型状态量分别为模型滞回位移z、模型加载位移x、激活点b,观测值为MFS模型恢复力,结构状态方程和观测方程如式(6)~(7)所示。
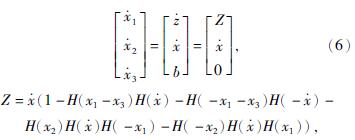
式中:x——加载位移;
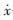 ——加载速度;
——加载速度;
H(x)——海维赛德阶跃函数。
y=KxA+(1-A)(1-Q)KR(x)+ (1-A)QKx1+WR。(7)
利用四阶Runge-Kutta积分算法将式(6)转化为离散状态方程,加入过程噪声WQ,过程噪声WQ和观测噪声WR分别为均值为零的高斯白噪声,过程噪声WQ和观测噪声WR的协方差矩阵分别为V、W。x^0为系统初始预估状态量,P0为初始预估协方差矩阵,实验加载速度x·由位移差分确定,过程噪声协方差V、观测噪声协方差W、系统预估状态量x^0、初始预估协方差矩阵P0具体取值如式(8)~(11)所示。
V=10-25I3,(8)
式中,I3——3×3的单位矩阵。
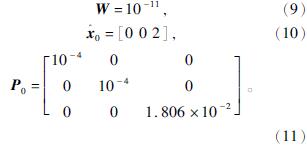
本次模拟加载速度由式(12)近似计算得到
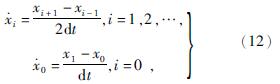
式中,dt——积分步长,其值为0.01 s。
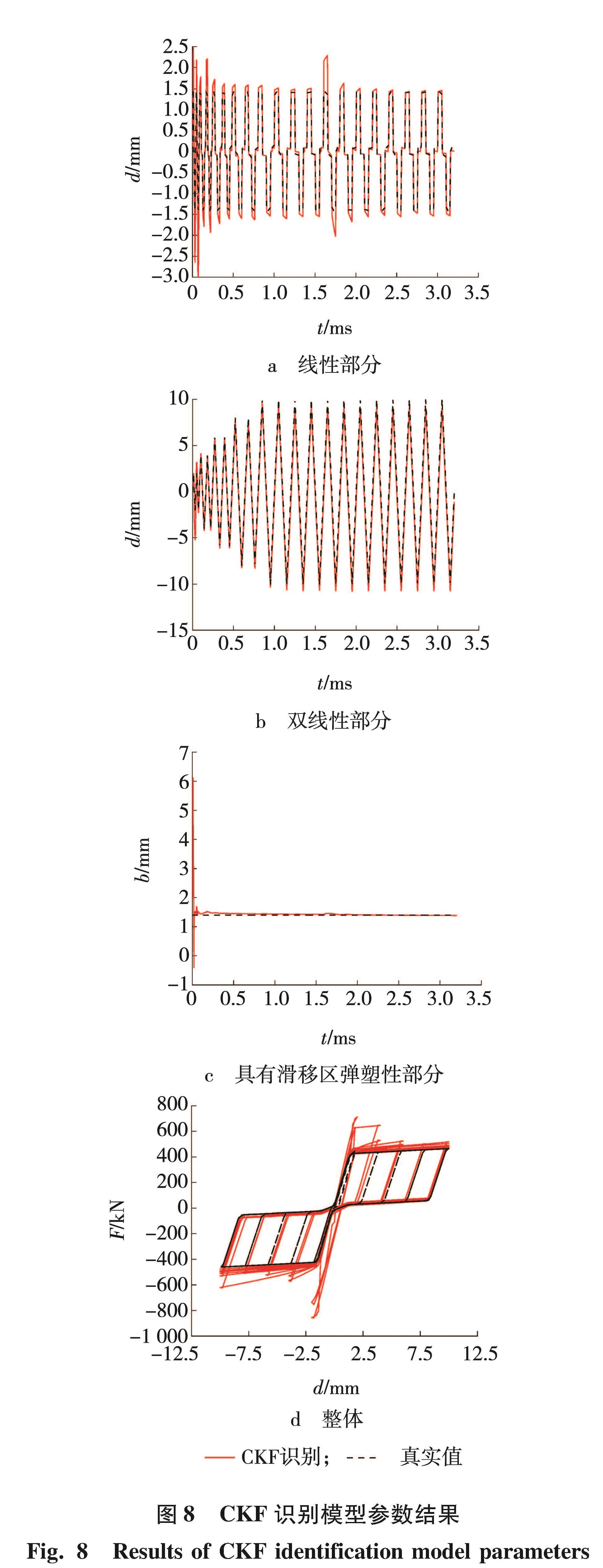
3.2 仿真结果与分析通过CKF对MFS模型参数进行识别,通过识别结果与模型参数真实值进行对比,识别仿真结果如图8所示。仿真计算耗时1.058 s,可见该算法具有较高的计算效率。从图8可以看出,CKF可以快速识别模型参数,识别的模型参数滞回位移、加载位移、b、支撑轴向恢复力收敛速度快,且真实值与识别值误差较小,CKF识别模型参数值滞回位移、加载位移、b、支撑轴向恢复力相对误差分别为23.2%、3.6%、2.2%、14.8%,识别参数可以有效反应模型真实性能。
4 结 论
(1)通过对MFS模型参数敏感性分析,得到了MFS模型参数影响规律,建议激活点b值的取值范围为0<b<3.5 mm。初始刚度K>0。耗能率Q值取值范围为0<Q<1。模型激活后刚度比取值范围为0<A<1。
(2)采用CKF算法在线识别MFS模型参数,结果表明,该算法具有较高的参数识别精度和计算效率,识别的参数能够反映MFS模型真实的滞回特性。
- [1] Bruneau M, Chang S E, Eguchi R T, et al. A framework to quantitatively assess and enhance the seismic resilience of communities [J]. Earthquake Spectra, 2003, 19(4): 733-752.
- [2] 池 沛, 董 军, 彭 洋, 等. 一种新型自复位耗能拉索支撑的理论研究与数值分析 [J]. 振动与冲击, 2016, 35(21): 171-176.
- [3] Ma H, Yam M C H. Modelling of a self-centring damper and its application in structural control [J]. Journal of Constructional Steel Research, 2011, 67(4): 656-666.
- [4] Bouc R. Forced vibration of mechanical systems with hysteresis [C]. Proceedings of the Fourth Conference on Nonlinear Oscillation, Prague, Czechoslovakia, 1967.
- [5] Wen Y K. Approximate method for nonlinear random vibration [J]. Journal of the Engineering Mechanics Division, 1975, 101(4): 389-401.
- [6] Xu L H, Fan X W, Li Z X. Development and experimental verification of a pre-pressed spring self-centering energy dissipation brace [J]. Engineering Structures, 2016, 127: 49-61.
- [7] 徐龙河, 樊晓伟, 逯登成, 等. 预压弹簧自恢复耗能支撑恢复力模型与滞回特性研究 [J]. 工程力学, 2016, 33(10): 116-122.
- [8] Zhou Z, Xie Q, Meng S P. Hysteretic performance analysis of self-Centering buckling restrained braces using a rheological model [J]. Journal of Engineering Mechanics, 2016, 142(6): 04016032.
- [9] 樊晓伟, 徐龙河, 李忠献. 预压弹簧自恢复耗能支撑非线性原理模型参数识别及实验验证 [J]. 土木工程学报, 2018, 51(7): 29-35.
- [10] Zhang H M, Quan L M, Lu X l. Modified flag-shaped model for self-centering system and its equivalent linearization and structural optimization for stochastic excitation [J]. Engineering Structures, 2020, 215: 110420.
- [11] 王 涛, 李 勐, 孟丽岩. 容积卡尔曼滤波器的Bouc-Wen模型在线参数识别 [J]. 黑龙江科技大学学报, 2020, 30(5): 551-555.
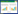 图 1 自复位摩擦耗能支撑机理
Fig.1 Self-centering energy dissipation brace mechanics
图 1 自复位摩擦耗能支撑机理
Fig.1 Self-centering energy dissipation brace mechanics