煤矿生产企业希望在供电系统发生高压电缆故障时,能够及时准确地排除电缆故障,避免永久故障发生时造成的突发停电和因电缆短路造成的各类事故。在矿井供电系统中,由于自然环境恶劣,当电缆发生单相接地故障时,接地电流产生的漏电火花可能引燃瓦斯尘埃,严重时会导致爆炸。矿井高压电缆发生故障时,需要更加快速准确发现故障点并加以修复; 由于矿井供电系统的供电方式为中性点不接地或中性点经消弧线圈接地,因此,发生单相接地故障时,流过接地点的电流很小,故障信号中的高频暂态信号不易获取。

目前,国内外对输电线路故障定位方面的研究日趋成熟,行波法及故障分析法等已经在实际工作场合中有了大量运用。基于小波变换模极大值的行波故障测距方法在矿用电缆故障定位中有着广泛的研究^[1-2],可以看出小波变换对小波基、分解尺度的选取比较灵活,不同的信号需要根据具体的条件来选取,而且由于小波固有的频率混叠现象会造成极大值的移位^[3],会导致极大值识别的误差,从而导致基于小波变换模极大值的矿用高压动力电缆故障定位方法不够精确,存在较大的误差。

基于传统的小波模极大值故障定位法使故障行波波头的检测不准确,导致故障定位误差较大。目前,基于VMD-TEO的故障定位方法在矿井供电系统中尚未得到应用。笔者将VMD-TEO相结合应用到矿用高压动力电缆故障行波波头信号的检测中,提出一种基于VMD-TEO的矿用高压动力电缆故障定位的方法。

VMD是Dragomiretskiy等^[4]提出的一种信号处理方法,VMD分解信号的核心思想是将信号的分解过程转移到变分框架内^[5],通过迭代搜寻变分模型的最优解,获解各个模态分量的中心频率与带宽。

变分模态的分解过程主要包括两个方面^[6-9]。

(1)变分问题的构造

构造变分问题需要寻找目标函数,设待分析的信号为f,通过VMD分解,将信号分解为K个模态函数u_k(t),假设每个模态都具有各自的中心频率与有限带宽,使每个模态的估计带宽之和最小。则对应的约束变分问题模型表达式为

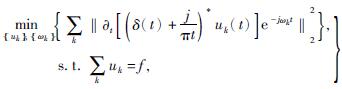(1)

式中:{u₁,u₂,…,u_k}——分解得到的k个IMF分量;

{ω₁,ω₂,…,ω_k}——各分量的中心频率;

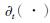——Hilbert变换;

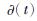——单位脉冲信号。

(2)变分问题的求解

引入Lagrange乘法算子λ(t)和二次惩罚因子α,所得增广Lagrange函数表达式为

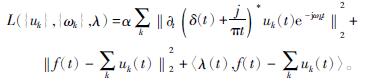(2)

通过交替方向乘子算法,求取增广Lagrange函数的鞍点,即为最优解。更新uⁿ⁺¹_k、ωⁿ⁺¹_k 和λⁿ⁺¹_k。uⁿ⁺¹_k的取值可表述为

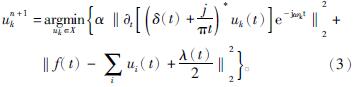
为了简便起见,认为ωⁿ_k=ωⁿ⁺¹_k,则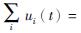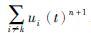,将式(3)转换到频域为

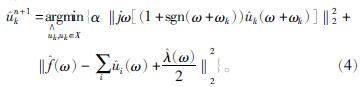
将式(4)中的第一项的ω用ω-ω_k代替,则可得

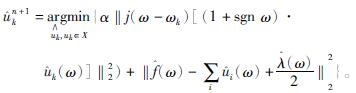(5)

将式(5)表示为积分区间为[0,∞]的积分形式

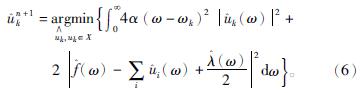
二次优化式(6),可以得到频率的解为

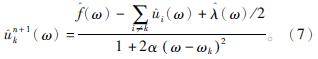
同理,对中心频率ωⁿ⁺¹_k进行求解,表达式为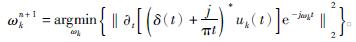

同上,优化可得

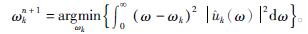(8)

对式(8)求解,可得最终中心频率为

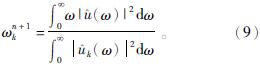
VMD算法流程如图1所示。由图1可见,VMD算法的计算步骤分为6步。

图1 VMD算法流程
Fig.1 Flow of VMD algorithm

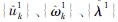(1)初始化和n=0;

(2)n=n+1,开始执行循环;

(3)根据式(7)、(9)更新u_k和ω_k;

(4)k=k+1,判断是否k=K,若是,则循环结束,若不是,则重复步骤(3);

(5)根据式(10)更新λ,

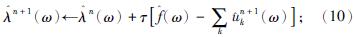
(6)根据式(11)判断是否满足迭代停止条件,若满足,则迭代停止,得到K个IMF分量。若不满足,重复步骤(2)至(5);

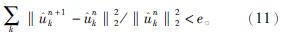
Teager 能量算子^[10-12]是一种信号分析算法,计算量小,能够快速准确地追踪信号能量,对信号的瞬时变化具有良好自适应能力。根据TEO的特点,获取分解后高频信号的瞬时能量谱,提取瞬时能量谱上首个峰值对应的时刻,即为故障初始行波到达检测点的时刻。

对于连续信号s(t),其能量算子的定义为

ψ[s(t)]=s'2(t)-s(t)s″(t),

式中:s'(t)——一阶导数;

s″(t)——二阶导数。

对于离散信号s(n),其能量算子的定义为

ψ[s(n)]=s²(n)-s(n+1)s(n-1)。

主要步骤如下:

(1)同步采集故障后M、N两侧检测点的A、B、C三相暂态电压行波信号;

(2)通过karenbauer相模变换,解除相间的耦合影响,得到行波线模、零模分量;

(3)选取行波线模分量进行VMD分解,得到K个IMF分量;

(4)选取IMF分量中的高频模态分量进行TEO分析;

(5)获取高频模态分量的Teager瞬时能量谱;

(6)通过Teager瞬时能量谱,可以得到故障行波到达M、N两侧检测点时刻。

利用Matlab/Simulink工具箱建立一个简化的3条出线的35 kV中性点不接地的单端电源的矿用高压供电网络的仿真模型,如图2所示。

由图2可知,35 kV的电源电压,经过三相变压器降压到10 kV向电缆供电,三条出线的高压动力电缆长度均设置为25 km且将线路l₃设为故障线路,电缆采用分布参数模型,线路的参数如表1所示。

图2 矿用高压供电网络仿真模型
Fig.2 Simulation model of mine high voltage power supply network

表1 分布式线路模型参数
Table 1 Distributed line model parameters

线路左侧为M侧,右侧为N侧。由仿真模型可知,线路l₃由两部分组成,改变线路l₃的长度,可以模拟不同故障位置,通过故障模块模拟不同故障类型和过渡电阻。采样频率为1 MHz,仿真时间为0.2 s,设置线路l₃发生故障发生的时间为0.10 s小于0.15 s。

设置故障点距离M侧14 km,同步采集故障后M、N两侧的A、B、C三相电压暂态行波信号,由于在三相系统中,相间存在耦合关系。利用Karenbauer相模变换解耦得线模与零模分量的表达式为

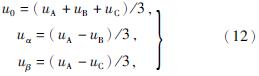
式中:u₀——零模分量;

u_α 、u_β——线模分量。

由于零模分量容易受集肤效应的影响,造成零模分量的衰减较为严重,不利于行波波头的检测,因此,文中选择线模分量u_a进行分析,不考虑参数的频率相关性时,线模分量的波速与正序分量的波速相近且波速较为稳定,其波速表达式为

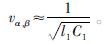
采用VMD分解线模分量u_a,选取分解后的高频分量分析Teager能量值,通过TEO瞬时能量谱获取故障行波到达时刻。VMD参数设置K=4、α=2 000、τ=0,故障时M、N两侧的线模信号及其VMD分解结果和高频分量的Teager能量值分析如图3所示。

图3 M侧的线模信号及其VMD分解结果
Fig.3 Line mode signal at M side and its VMD decomposition results

在研究电缆故障定位时,如何获取所需要的故障信息是研究的关键所在。通常情况下,信号的高频部分中含有丰富的故障信息,这些高频部分中的故障信息是电缆故障定位的关键因素,因此,文中选择IMF₁分量来进行Teager能量值计算,如图4所示。

图4 M侧的 IMF1分量及TEO的瞬时能量谱
Fig.4 M IMF1 component and instantaneous energy spectrum of TEO

通过TEO提取IMF₁分量瞬时能量变化的极大值,提取对应的横坐标如图5所示,即可得到故障行波到达M侧检测点的时间。

同理,可以得到故障时,N侧的线模信号s及其VMD分解结果; N侧的IMF₁分量及TEO的瞬时能量谱如图6和7所示。N侧的IMF₁分量的TEO瞬时能量谱峰值所对应的时刻,如图8所示。

图5 M侧IMF1分量的TEO瞬时能量谱峰值
Fig.5 Time corresponding to peak value of TEO instantaneous energy spectrum of IMF1 component at M side

图6 N侧的线模信号及其VMD分解结果
Fig.6 Line mode signal on N side and its VMD decomposition results

图7 N侧的 IMF1分量及TEO的瞬时能量谱
Fig.7 IMF1 component on N side and instantaneous energy spectrum of TEO

由图5和8可见,线路故障的初始行波达到M侧和N侧的时刻,分别记为t₁和t₂。双端行波测距即可以求得故障定位距离为

d=(l-v(t₂-t₁))/2,(13)

式中:d——故障点距离M侧的距离,km;

l——线路长度,L=25 km;

v——行波的传播速度,文中v=2.899×10⁸ m/s。

将图5和8中初始行波到达M侧和N侧的时刻代入式(13)中,求得故障点距离M侧的距离为

d=14.094 km。

图8 N侧的IMF1分量的TEO瞬时能量谱峰值所对应的时刻
Fig.8 Time corresponding to peak value of TEO instantaneous energy spectrum of IMF1 component on N side

由相对误差公式为

e=(|d_j-d_s|)/(d_s)×100%,(14)

式中:d_j——计算距离;

d_s——故障实际距离。

相对误差为

e=(|14.094-14|)/(14)×100%=0.671%。

为了验证基于VMD-TEO的矿用高压动力电缆故障定位方法较小波变换模极大值故障定位方法有更高的可靠性和精确度,分别以不同的故障距离、故障类型进行对比分析,由于篇幅有限,文将过渡电阻设50 Ω,对比结果如表2和3所示。

由表2和3可知,在相同故障距离、故障类型与过渡电阻的的条件下,基于VMD-TEO算法的故障定位方法比小波变换模极大值的故障定位方法的测距结果相对误差小、精确度更高。

表2 基于小波变换模极大值的故障定位结果
Table 2 Fault location results based on wavelet transform modulus maximum method

表3 基于VMD-TEO算法的故障定位结果
Table 3 Fault location results based on VMD-TEO algorithm

(1)针对矿井供电系统中,由于中性点的运行方式,当系统发生单相接地故障时,流过接地点的电流很小,很难获取到故障信号中的高频暂态分量,使行波波头的检测不准确,导致故障定位误差较大。通过提出一种基于VMD-TEO的矿用高压动力电缆故障定位的方法,将VMD-TEO相结合应用到矿用高压动力电缆故障行波波头信号的检测,获取初始行波到达检测点的准确时间,代入测距算法进而确定故障位置。

(2)基于小波变换模极大值故障定位的相对误差均大于1%,而基于VMD-TEO算法故障定位的相对误差均小于1%,提高了定位精确度,更有利于电缆故障的排除。