随着风能的利用率不断提高,风力发电以其独特的优势得到迅速发展。伴随电网中新能源接入数量的增加,架设更多更长的输电线路会向电网中引入大量线路阻抗,使电网逐渐呈现出弱网特性[1-3],风电场阻抗与电网阻抗的相互影响导致系统失稳,为解决这一问题,高本锋[4]、宋瑞华[5]和苏田宇[6]提出调整控制器参数法、附加阻尼法与配置机网侧阻尼控制等多种方法改善风电并网后系统的运行稳定性。Cespedes等[7]指出可通过更改附加的滤波装置实现系统的稳定运行,但采用单电感滤波器需要较大电感值的电感,其滤波器成本高、体积大且动态性能差,已经不符合大规模风电并网的需求[8-9],通过LCL型滤波器能够选取较小的电感实现同样的滤波效果[10]。Wen等[11]给出了阻抗法的单电感型滤波器的并网逆变器阻抗模型,其滤波电感值较大。夏丹妮[12]指出了通过阻抗法的基于LC型并网逆变器的直驱风电机阻抗模型,其小信号模型未考虑电容电流支路。
为了进一步提高并网稳定性,减小直驱风电机并网成本,笔者以阻抗法的LCL逆变器型直驱风电机为研究对象,综合锁相环、电流内环与功率外环的特性,在两相旋转坐标系下推导其等效阻抗模型,通过广义奈奎斯特判据分析部分参数对稳定性的影响。
1 直驱风电机网侧小信号模型1.1 直驱风电机基本原理直驱风力发电机原理如图1所示。
直驱风电机由风轮、发电机、变流器及其控制系统组成。在整个直驱风力发电机运行时,可以忽略风轮、轴系产生的机械振荡,将风轮、发电机和发电机侧变流器通过戴维宁定理等效为一个直流电压源,通过调整电压值的大小实现控制功率的大小[8,12]。
1.2 dq坐标系下的开环小信号模型直驱风电机网侧逆变器的主电路结构如图2所示,其中,Udc为直流电压稳态值,Cdc为直流电压母线稳压电容,S1~S6为反并联自关断二极管,Lf1、Lf2和Cf分别为LCL滤波器的滤波电感与滤波电容,Rf1、Rf2和RC分别为LCL滤波器上滤波电感与滤波电容上的寄生电阻,Lg为网侧电感,Rg为网侧电感上的寄生电阻,ea、eb和ec分别为网侧三相电压。
为了从并网点处得到整个系统的阻抗模型,需要先得到其传递函数,根据图2所示结构进行派克变换,得到在两相旋转坐标系(dq坐标系)下的小信号模型,如图3所示。
图3中,Dsd、Dsq、dsd和dsq分别表示在两相旋转坐标系下主电路电压的稳态值与扰动值,udc为直流电压扰动值,isd、isdc和usd,isq、isqc和usq分别表示两相旋转坐标系下d轴与q轴并网点电流扰动值、电容支路电流扰动值和并网点电压扰动值。
由图3可以看到
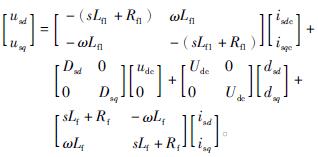
对于开环输出阻抗Zout,可以令dsd、dsq和udc为0,则有
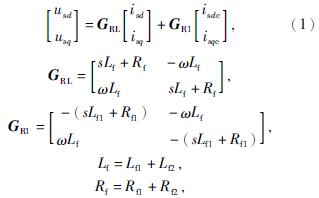
式中:GRL——LCL滤波器阻抗传递函数矩阵;
GR1——LCL滤波器逆变电路侧阻抗传递函数矩阵;
Lf——LCL滤波器等效电感;
Rf——LCL滤波器等效电阻。
对于开环主电路占空比到并网点电流的传递函数Gid,可以令usd、usq和udc为0,则
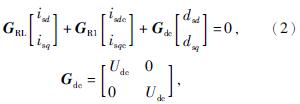
式中,Gdc——dq坐标系下直流电压稳态值的传递函数矩阵。
根据基尔霍夫电压定律,并网点处电压扰动关系为
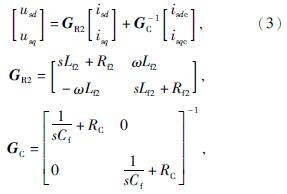
式中:GR2——LCL滤波器网侧阻抗传递函数矩阵;
GC——LCL滤波器电容支路阻抗传递函数矩阵。
将式(3)分别代入式(1)和(2),可以得到并网点电压到并网点电流的传递函数为
Zout=(GRL-GR1GCGR2)/(E-GR1GC),
占空比到并网点电流的传递函数为
Gid=(Gdc)/(GR1GCGR2-GRL)。
此时,开环情况下的主电路传递函数如图4所示。其中,us为主电路中的电压扰动值,is为主电路电流扰动值,ds为主电路占空比扰动值。
1.3 dq坐标系下的闭环模型
在并网逆变器的控制策略中,通过锁相环(PLL)获取控制系统与电网系统的相位信息,使并网逆变器与电网同步。而锁相环内部使用PI控制器进行控制,原理如图5所示。图中,ua、ub和uc分别为锁相环采样点处的三相电压,ud和uq分别为经过派克变换后的d轴和q轴电压,θPLL为主电路系统与控制系统间在扰动存在时的相位差。
主电路系统与控制系统间在扰动存在时的相位差θPLL可以定义为
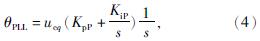
式中:KpP——锁相环PI调节器比例系数;
KiP——锁相环PI调节器积分系数。
当电网侧出现扰动时,电网与控制系统就会出现相位差,两坐标系之间的相位关系矩阵为
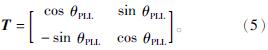
由于扰动量导致的相位变化很小,因此,可以将cos θPLL≈1,sin θPLL≈θPLL,则式(5)为
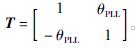
主电路与控制电路的关系为
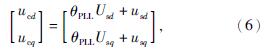
式中:ucd——控制电路中d轴扰动值;
ucq ——控制电路中q轴扰动值;
Usd——主电路中d轴电压稳态值;
Usq——主电路中q轴电压稳态值。
联立式(4)和(6),可得
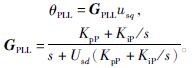
式(6)可以变为
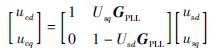
因此,可以得到主电路电压、电流和占空比到控制电路电压、电流和占空比的传递函数矩阵
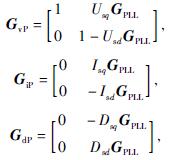
式中:Isd——主电路中d轴电流稳态值;
Isq——主电路中q轴电流稳态值;
Dsd——主电路中d轴占空比稳态值;
Dsq——主电路中q轴占空比稳态值;
GPLL——锁相环传递函数矩阵。
含锁相环的主电路控制模型如图6所示。图中,ic为控制电路电流扰动值,dc为控制电路占空比扰动值。
此时的输出阻抗为
ZoP=(Z-1out+GidGdP)-1。
除了通过锁相环对直驱风电机系统的并网进行控制,还通过电流内环和功率外环两个环节实现系统的控制。在电流内环中,通过一个PI调节器实现对电流的控制,电流内环控制矩阵为
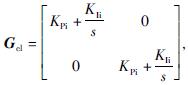
式中:KPi——电流内环PI调节器比例系数;
KIi——电流内环PI调节器积分系数。
在系统通过派克变换从三相静止坐标系到两相旋转坐标系的变换后,电流内环还会存在正负序电流的耦合,因此,还需要加入解耦矩阵:
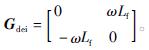
含锁相环与电流内环的主电路控制模型如图7所示。图中,iref为电流参考值。由于该模型为小信号模型,为了尽可能减小使扰动值,故将电流参考值设为0。
此时,输出阻抗为
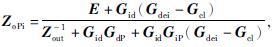
式中,E——二阶单位矩阵。
为了实现对电流内环中的参考电流进行更加准确的控制,现选择在电流内环的控制器之前加入功率外环,确保逆变器产生正确的无功功率和有功功率。在控制电路的两相旋转坐标系中,有功功率与无功功率的表达式为
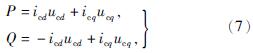
式中:P——有功功率;
Q——无功功率;
icd——控制电路中d轴电流稳态值;
icq——控制电路中q轴电流稳态值;
ucd——控制电路中d轴电压稳态值;
ucq——控制电路中q轴电压稳态值。
当系统稳定时,通过对式(7)进行线性化可以得到:
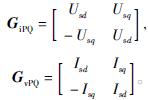
式中:GiPQ——电流到功率的传递函数矩阵;
GvPQ——电压到功率的传递函数矩阵;
Isd——主电路中d轴电流稳态值;
Isq——主电路中q轴电流稳态值;
Usp——主电路中d轴电压稳态值;
Usq——主电路中q轴电压稳态值。
功率外环的PI控制器传递函数矩阵为
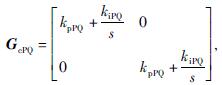
式中:KpPQ——功率外环PI调节器比例系数;
KiPQ——功率外环PI调节器积分系数。
含锁相环、电流内环与功率外环的主电路控制模型如图8所示,Pref、Qref为有功功率与无功功率参考值,与电流参考值选取目的一致,故设为0。
此时的输出阻抗为
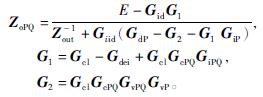
在传统的直驱风电机并网中,采用单个电感进行滤波。为了更加优异的并网效果,需要不断增加电感值的大小,随着电感大小的增加,电网强度便会随之下降,导致系统的动态性能同步降低。将通过对比单电感型滤波器和LCL型滤波器在直驱风电机并网中的实际效果。
2.1 LCL型滤波器谐振根据图2所示的直驱风电机并网侧电路结构,其基尔霍夫电压方程为
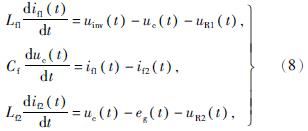
式中:if1——滤波器逆变器侧电感电流值;
if2——滤波器网侧电感电流值;
uc——滤波器电容支路电压值;
uinv——逆变器输出电压值;
uR1——滤波器逆变器侧电感寄生电阻值;
uR2——滤波器网侧电感寄生电阻值;
eg——并网侧电压值。
为了简化计算,忽略滤波器寄生电阻,对式(8)进行拉普拉斯变换可得,逆变器输出电压到并网电流的传递函数为
HLCL=1/(s3Lf1Lf2Cf+s(Lf1+Lf2))。(9)
由式(9)可知,传递函数HLCL的分母不含二次项,此时,系统易受到尖峰谐振的干扰,现通过在电容支路添加一个电阻RC,获得新的传递函数矩阵为
HRL=(sCfRC+1)/(s3Lf1Lf2Cf+s2(Lf1+Lf2)CfRC+s(Lf1+Lf2))。
同理,可以得到单电感滤波器的逆变器输出电压到并网电流传递函数为
HL=1/(sL)。
在Matlab/Simulink中对上述三种情况下的幅频特性分析结果如图9所示,单滤波电感滤波器的电感值为3 mH,LCL型滤波器电感值为0.3 mH。含电容支路电阻的LCL型滤波器电感值为0.3 mH。
从图9可以看出,三种滤波器具有相近的滤波效果,对于电容支路不含电阻的LCL型滤波器,在某一特定频率下会出现尖峰,造成系统失稳,在引入电容支路电阻后,尖峰得到抑制,保证系统能够在高频段下稳定运行。
2.2 阻抗模型
单电感型滤波器与LCL型滤波器进行对比如图 10所示。
由于dq、qd分量的幅值与相位趋势与dd、qq轴相近,故仅对dd与qq轴,通过其波德图分析稳定性。由于在相同控制模式与控制参数下,单电感滤波器需要更大值的电感才能保证系统稳定,将LCL型滤波器的电感值调整至单电感型滤波器相同值,通过Matlab/Simulink搭建不同滤波器下的直驱风电机模型,由图 10可以看到,在1到100 Hz内,无论d轴q轴的曲线都有较高程度的拟合; 在100到1000 Hz内,dq分量和qq分量的负序范围都有明显增大,其中,电容支路不串接电阻的LCL型滤波器变化尤为明显,这种情况下系统极易失稳,电容支路串接电阻的LCL滤波器对整个系统的稳定效果更优,可以保证直驱风电机系统并网的稳定性需求。
3 仿真与结果分析由于在风电并网中,电网显感性,呈现弱电网状态,控制器参数会对并网稳定性产生不可忽略的影响。为了探究不同控制器参数下的LCL型并网逆变器的直驱风电机系统的稳定性,通过广义奈奎斯特判据(GNC)进行论证。需要建立直驱风电机输出阻抗模型与网侧阻抗模型的回比矩阵N(s),根据广义奈奎斯特判据对系统稳定性的判别依据,当回比矩阵N(s)的GNC曲线围绕(-1,j0)点时,系统失稳,出现振荡的风险加大; 反之,系统稳定[12-13]。关系式为
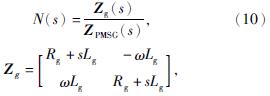
式中:Zg(s)——电网等效阻抗矩阵;
ZPMSG(s)——直驱风电机等效阻抗矩阵;
Rg——电网等效电阻;
Lg——电网等效电感。
主电路仿真参数:PN为2 MW,Uabc为690 V,Lf1为0.8 mH,Lf2为0.8 mH,Cf为20 μF,Cdc为4 700 μF,Udc为1 200 V和Lg为0.6 mH。控制电路参数:KpP为40,KiP为180,KpPQ为0.5,KiPQ为2,KPi为0.6,KIi为35。
3.1 电网电感对直驱风电机稳定性的影响由于电网阻抗与主电路的各项参数会产生耦合现象,电网等效电感值越大,弱网特性越明显[12,14],对系统的稳定运行的状态影响越大。稳定运行下的回比矩阵广义奈奎斯特图如图 11所示。电网电感分别为0.5、1.0与1.5 mH时的奈奎斯特图见图 12。
由图 11、12可见,此时曲线没有包围稳定判别点(-1,j0),文中均将采用局部放大图对稳定性进行分析。在直驱风电机系统并网时,线路上的寄生电阻较小,电网强弱主要受线路上的电感影响。通过图 12可见,当电网强度变弱,即电网电感逐渐增大,由0.5 mH增大至1.5 mH时,红色实线逐渐包围稳定判别点。根据广义奈奎斯特稳定性判据,系统从稳定状态过渡到了不稳定状态,如果继续增加电网电感,系统将出现不可抑制的振荡。
3.2 控制器参数对直驱风电机稳定性的影响通过将讨论锁相环比例系数与电流环比例系数对系统的影响。电网电感为0.5 mH,锁相环比例系数分别为40、80、120时的奈奎斯特曲线如图 13所示。
与不同滤波器的波德图反映出的结果近似,由于在两相旋转坐标系(dq坐标系)中推导的阻抗模型已计及解耦,因此dq与qd两个通道的耦合分量在不同锁相环比例系数下的波德图显示出的变化趋势与dd与qq分量近似,故在这里仅展示dd分量的幅值与相位和qq分量的幅值与相位。由图 13可见,锁相环比例系数从40到120变化时对系统的稳定性影响不大。
为了保证结论的正确性,结合不同比例系数下的波德图进行判定,如图 14所示。
图 14 不同锁相环比例系数的直驱风电机波德图
Fig.14 Bode of PMSG impedance with different proportionality coefficient of PLL
由图 14可见,综合不同锁相环比例系数的奈套斯特图与波德图,不同锁相环比例系数下,曲线相差近似,没有曲线在负序范围内有较大变化,因此,可以断定,锁相环比例系数从40变化到80,再变化到120时对系统的稳定性影响不大。
电网电感为0.5 mH,锁相环比例系数为40,电流内环比例系数分别为0.6、0.4和0.2时的奈奎斯特曲线如图 15所示。
由图 15可见,电流内环比例系数从0.6减小到0.2后,广义奈奎斯特曲线中蓝色线逐渐包围稳定判别点,系统从稳定状态逐渐过渡到不稳定状态,如果继续减小电流内环的比例系数,系统将失稳振荡。
4 结 论运用了阻抗分析法建立了基于LCL型并网逆变器的直驱风电机的等效数学模型,推导了直驱风电机的小信号阻抗公式,在Matlab/Simulink中分别分析了直驱风电机并网滤波器的幅频特性,以及不同并网逆变器、滤波器的稳定性。
(1)并网逆变器应用于直驱风电机并网时,电感值为3 mH的单电感滤波器才能与电感值为0.3 mH 的LCL型滤波器达到相同的稳定效果,在选择电感值为0.3 mH的滤波电感时,LCL型滤波器的滤波效果更稳定。
(2)当电网电感由0.5 mH增大至1.5 mH及电流环比例系数由0.6减小至0.2时,直驱风电机系统的奈奎斯特曲线逐渐包围稳定判别点(-1,j0),说明系统稳定性开始下降。
(3)锁相环比例系数由40增大至120时,奈奎斯特曲线始终未包围判别点,对系统稳定性影响不大。由此可见,直驱风电机系统并网的过程中应选取合适的控制参数来实现系统的稳定性。
- [1] Roinila T, Messo T. Online grid-impedance measurement using ternary-sequence injection[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 5097-5103.
- [2] 曾志杰, 肖华锋, 高 博, 等. 并网逆变器小信号建模简化方法与应用[J]. 中国电机工程学报, 2020(21): 7002-7012
- [3] 万玉良, 朱 玲, 项 颂, 等. 直驱风电机组与弱电网交互作用稳定分析[J]. 中国电力, 2019, 52(9): 118-125.
- [4] 高本锋, 崔意婵, 邵冰冰, 等. 直驱风电机组全运行区域的次同步振荡特性分析[J]. 电力建设, 2020, 41(2): 85-93.
- [5] 宋瑞华, 郭剑波, 李柏青, 等. 基于输入导纳的直驱风电次同步振荡机理与特性分析[J]. 中国电机工程学报, 2017, 37(16): 4662-4670.
- [6] 苏田宇, 杜文娟, 王海风. 并网风电场次同步振荡抑制措施研究综述[J].南方电网技术, 2018, 12(04): 60-69.
- [7] Cespedes M, Sun J. Impedance modeling and analysis of gridconnected voltage-source converters[J].IEEE Transactions on Power Electronics, 2014, 29(3): 1254-1261.
- [8] 李奕欣, 赵书强, 马燕峰, 等. 三相LCL型并网逆变器的阻抗建模及特性分析[J]. 电力自动化设备, 2019, 39(7): 107-113.
- [9] Bruno B, Karel B, Jeroen K, et al. Model-based generation of low distortion currents in grid-coupled PWM-inverters using an LCL output filter[J]. IEEE Transactions on Power Electronics, 2006, 21(4): 1032-1040.
- [10] 郭小强, 邬伟扬, 顾和荣, 等. 并网逆变器LCL接口直接输出电流控制建模及稳定性分析[J]. 电工技术学报, 2010, 25(3): 102-109.
- [11] Wen B, Boroyevich D, Burgos R, et al. Analysis of D-Q small-signal impedance of grid-tied inverters[J]. IEEE Transactions on Power Electronics, 2015, 31(1): 1-4.
- [12] 夏丹妮. 直驱风电机组次同步振荡分析与抑制策略研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.
- [13] 苏勋文, 岳 兵, 安鹏宇, 等. 双馈风机的小信号阻抗模型与稳定性[J].黑龙江科技大学学报, 2020, 30(3): 302-308.
- [14] 徐海亮, 聂 飞, 王诗楠. 弱电网下永磁风机网侧变流器频率耦合效应关键作用因子评估及控制对策[J]. 电网技术, 2021(5): 1687-1697.
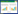 图 1 直驱风力发电机原理
Fig.1 Schematic diagram of PMSG
图 1 直驱风力发电机原理
Fig.1 Schematic diagram of PMSG