在“碳达峰”、“碳中和”等国家层面的承诺中不难看出,未来的电源研发领域在高频高效领域有广阔的空间。图腾柱PFC拓扑以其组件数量少、共模干扰低、最低传导损耗、最高效率等优点在功率因数校正圈内备受关注。氮化镓(GaN)、碳化硅(SiC)等第三代宽禁带半导体器件的出现,将制约图腾柱拓扑的第一大阻力二极管反向恢复问题迎刃而解,使图腾柱PFC在大功率场合的应用成为可能。功率等级的增加必然会带来传导损耗增大,因此,传统图腾柱无桥PFC拓扑中的二极管注定会被取代,业界最常见的解决方案是用导通电阻较小的MOSFET替代,但依旧无法解决开关损耗高带来的温升和过零点畸变等问题,系统高频化难以实现。针对这些问题,笔者提出了一种半周期高频半周期工频的控制策略,将传统图腾柱无桥PFC拓扑中的二极管用功率开关管替代,应用数字锁相技术在输入电压过零点处切换前后桥臂的频率等级,没有快慢桥臂之分。开关管在高频和工频模式下切换工作,有效解决器件的温升问题,电压过零点处工频高电平切换高频时脉冲由宽渐窄、工频低电平切换高频时由窄渐宽,高频向低频切换时类似,此种脉冲切换方式避免了占空比突变,过零点畸变问题得到有效解决。笔者研究图腾柱PFC工作于连续导电模式(CCM),分析电路的工作原理,理论分析电路控制算法及公式推导,对改进后的电路拓扑进行建模,通过搭建样机进行调试验证。
1 电路模态与控制策略系统采用改进后的图腾柱无桥PFC结构,具体方案原理如图1所示。电路由泵升电感L,开关管Q1、Q2、Q3、Q4及滤波电容Co构成,与传统图腾柱结构不同的是后桥臂的二极管被可控管替代。高功率密度的需求促使开关电源向高频化发展,硬开关下的高频化带来较大的开关损耗,TCM模式控制虽能实现软开关,但控制算法过于复杂实现困难。采用半周期高频半周期工频的驱动方式,均衡器件高频硬开关带来的温升以保证系统长时间可靠运行,以及过零点处无占空比突变的特性有效解决过零点处相关问题。通过电路拓扑模态、系统控制策略及电路小信号建模三个方面进行原理介绍,验证系统的稳定性与可行性。
1.1 CCM图腾柱PFC模态
CCM模式下图腾柱PFC工作模态如图2所示。由图2可见,根据输入电压的正负半周及电感的充放电可将电路分为四个模态。
模态1输入正半周时,开关管Q1、Q3关断,Q2、Q4导通,电感L通过Q2、Q4由电网Uin给其储能,负载由电容Co供电。此时电路工作状态与Boost电路的储能阶段一致。
模态2输入正半周时,开关管Q1、Q4导通,Q2、Q3关断,电网Uin与电感L一起经Q1、Q4给负载和电容Co供电。此时电路工作状态与Boost电路的放能阶段一致。
模态3输入负半周时,开关管Q1、Q3关断,Q2、Q4导通,电感L通过Q4、Q2由电网Uin给其储能,负载由电容Co供电。此时电路工作状态与Boost电路的储能阶段一致。
模态4输入负半周时,开关管Q2、Q3导通,Q1、Q4关断,电网Uin与电感L一起经Q3、Q2给负载和电容Co供电。此时电路工作状态与Boost电路的放能阶段一致。
系统在一个工频周期内各个开关管的驱动脉冲示意如图3所示。
在输入电压正半周时,前桥臂作高频桥臂,储能管Q2的脉冲脉宽呈宽渐窄再渐宽变化,续流管Q1与Q2脉冲为互补波形,脉宽呈窄渐宽再渐窄变化。后桥臂作工频桥臂,开关管Q3的脉冲保持常低,相对的开关管Q4则保持常高。在输入电压由正半周进入负半周时,Q1脉冲由窄脉冲变为常低,Q2脉冲由宽脉冲变为常高,Q3脉冲由常低变为窄脉冲,Q4脉冲由常高变为宽脉冲。输入电压由负半周进入正半周时与之情况相似此处不再赘述。观察各个脉冲波形后不难发现,在输入电压过零点处并无脉宽突变的情况。系统采用该调制方式,不仅能够有效均衡开关管的温升,还能有效解决输入电压过零点处的相关问题。在输入电压负半周时,前桥臂作工频桥臂,后桥臂作高频桥臂,具体脉冲与输入电压正半周相似,此处不再作具体阐述。
1.2 系统控制策略由图2可见,电路中的图腾柱无桥PFC采用的是CCM模式下基于平均电流的电压前馈双闭环控制策略。直流输出电压采样后与给定电压做误差PI后和数字锁相获得的与输入电压同相位的单位馒头波相乘后作电流给定,此为电压环。将得到的电流给定与电流采样获得的电流反馈信号做误差PI后为双闭环调制信号,此为电流环。输入交流电压峰值与输出电压幅值的比值与锁相获得的单位馒头波相乘得到电压前馈信号。双闭环调制信号与电压前馈信号一起构成总的调制信号,与三角基波比较后就可得到驱动脉冲。系统使用的主控芯片是TI公司的Piccolo微控制器TMS320F28035,利用基于二阶广义积分的数字锁相技术,再结合输入电流采样及输出电压采样,经过处理及算法计算完成对系统的实时控制。文中对开关周期内的电感电流进行暂态分析及算法理论公式推导,如图4所示。电流值ia、ib、ic分别为开关周期内的起始电流、峰值电流及终止电流,D代表储能管的占空比,忽略死驱时间。
Uin=L(diL)/(dt)=L(ib-ia)/(DTs)。(1)
在电感L放能阶段,可得电路方程为
UO-Uin=L(diL)/(dt)=L(ib-ic)/((1-D)Ts),(2)
联立式(1)(2)可得
ic-ia=([Uin-(1-D)UO]Ts)/L。
若设终止电流ic为给定电流i*,起始电流ia为当前采样电流i,则可以得到从当前采样占空比的表达式为
D=1+(L(i*-i))/(TsUO)-(Uin)/(UO) 。
分析占空比的表达式可知,其受控于电感L电感量、开关频率、输入电压、输出电压及当前电流值和给定电流值控制,系统稳定时占空比主要受输入电压、当前电流值和给定电流值控制。
1.3 恒频CCM图腾柱的小信号建模由上述分析可知,改进后的图腾柱PFC与同步Boost变换器工作模态一致,以该拓扑进行建模分析。将状态空间平均方法(SSA)应用于如图5所示同步Boost变换器。
主开关管Q1导通和关断期间的等效电路分别如图6所示。
由图6可见,根据元器件特性关系式为

主开关管导通时间内有:
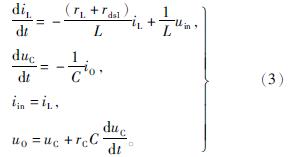
主开关管关断时间内有:

将式(3)乘以系数d,式(4)乘以d',然后两者相加,考虑到d+d'=1,可得平均状态空间方程组为

由于变换器工作于连续模式,可将平均变量等价为直流量和交流小信号量之和,利用此方法对式(5)进行线性化后,可得到时域状态空间方程的矩阵形式为

对矩阵方程进行拉普拉斯变换,求得输入到输出的关系为

令式(5)中的(diL)/(dt)和(duC)/(dt)等于零,可得各状态变量的稳态值为
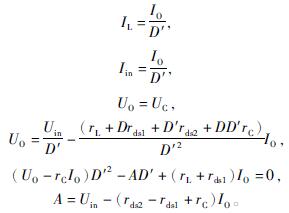
同步Boost变换器小信号等效电路如图7所示。结合上述分析,给出同步Boost变换器的等效小信号动态电路方程为

由变量稳态值的表达方程可知,同步Boost变换器的输出电容ESR对稳态工作点有影响。其影响反应在变换器模型中为输出端的串联电阻,在特定输出电压条件下要求增加占空比,在变换器设计时应予以考虑。通过对变换器小信号模型的分析及时域和频域公式推导,验证了半周期工频半周期高频控制策略的可行性和必要性。
2 实验验证为了验证文中方案设计的可行性及算法理论推导的正确性,搭建了一台实验样机如图8所示。交流输入电压Uin范围为176~264 V,直流输出电压UO为400 V,额定输出功率400 W满载时,要求输入功率因数PF大于0.98,输入电流总谐波畸变率THD小于5%,整机效率96%以上。
实验样机主要包括前级的共模EMI滤波器模块、主拓扑电路、单管单芯片的独立驱放电路和由比较器构成的硬件门限过流保护电路(触发后直接进TZ口),以及由反激构成的多路隔离电源的辅助电源模块等,经过多版迭代最终样机尺寸为15.73 cm×6.2 cm×1.62 cm,整机功率密度2.53 W/cm3,实现高功率密度要求。主开关器件选用GaN Systems公司耐压650 V和最大持续导通电流7 A的GS66502B,驱动芯片选用独立驱放的SI8271GB,辅助电源模拟控制芯片选取频率自动调节的NCP1253,泵升电感磁芯材质选用高磁导率的铁镍钼磁芯,电感量L取3 mH,滤波电容CO容量为200 μF。
样机工作在额定220 V交流输入,直流输出电压400 V和输出功率满载400 W时,样机散热方式为顶部铝制散热片散热,环境为无风机常温自然散热。实验样机满载运行时的温度分布如图9所示,可见样机运行时最高温度为80.12 ℃,并对温度分布进行了基于温度的柱状分析如图 10所示,从图 10可以看出,温度主要集中在40~60 ℃。
满载时输入输出波形如图 11所示。由图 11可知,满载输出功率时,交流输入电压、电流波形图以及输出电压。输入电压与输入电流波形重合度很高,满足对输入功率因数的要求,输入电流波形正弦化程度颇深且过零点处无明显异常,输入电流THD达到2.9%。整机的效率曲线如图 12所示。由图 12可见,峰值效率高达97.9%,实现对高效电源的要求。
3 结 论
(1)传统图腾柱无桥PFC拓扑中的二极管用GaN HEMT替代后,采用半周期高频半周期工频的控制策略,实现开关管的高低频切换,没有高频管和低频管的界定,有效均衡高频开关损耗引起的温升。
(2)针对电压过零点输入电流畸变的问题,采用半周期高频半周期工频的控制策略,能够实现工频周期内低脉冲与窄脉冲的切换和高脉冲与宽脉冲的切换,解决占空比突变问题,有效解决了输入电流过零点畸变。
- [1] Yu Z, Xia Y, Ayyanar R. A simple ZVT auxiliary circuit for totem-pole bridgeless PFC rectifier[J]. IEEE Transactions on Industry Applications, 2019, 7(3): 1-1.
- [2] 程章格. 基于氮化镓器件的电动汽车充电机中无桥PFC应用技术研究[D]. 重庆: 重庆大学, 2018.
- [3] Liu Z, Lee F C, Qiang L, et al. Design of GaN-based MHz totem-pole PFC rectifier[J]. Emerging & Selected Topics in Power Electronics IEEE Journal, 2016, 4(3): 799-807.
- [4] 经雯荔, 管乐诗, 王懿杰, 等. 高频AC/DC变换器优化控制策略研究[J]. 电源学报, 2020, 18(5): 60-71.
- [5] Zhang R, Liu S, Li B, et al. Totem-pole bridgeless boost PFC converter based on GaN HEMT for air conditioning applications[C]. 2018 2nd IEEE Conference on Energy Internet and Energy System Integration(EI2), IEEE, 2018.
- [6] Zhang B, Imaoka J, Shoyama M, et al. Study on zero-crossing conducted noise issue of totem-pole bridgeless PFC converter[C]. Future Energy Electronics Conference & Ecce Asia, IEEE, 2017.
- [7] 李力超, 何 维, 吴新科. 基于软开关图腾柱拓扑的AC/DC电源[J]. 电力电子技术, 2021, 55(2): 77-79.
- [8] 陈伟川. 基于V2G的双向AC-DC变换器及其锁相优化研究[D]. 厦门: 厦门理工学院, 2020.
- [9] Q Huang, Q Ma, R Yu, et al. Improved analysis, design and control for interleaved dual-phase ZVS GaN-based totem-pole PFC rectifier with coupled inductor[C]. 2018 IEEE Applied Power Electronics Conference and Exposition(APEC), IEEE, 2018.
- [10] 张 旬, 林志贤, 姚剑敏, 等. 基于GaN的图腾柱PFC电流过零点问题的研究[J]. 微电子学, 2019(4): 39-42.
- [11] 钱圣宝. 连续导通模式图腾柱无桥PFC变换器的分析与设计[D]. 南京: 东南大学, 2017.
- [12] 徐厚建. 临界连续模式高效率无桥PFC整流器研究[D]. 杭州: 浙江大学, 2018.
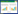 图 1 拓扑原理
Fig.1 Topology principle
图 1 拓扑原理
Fig.1 Topology principle












