采煤机截割煤岩时,截割部承受载荷复杂[1],对传动系统和牵引部形成冲击,因此,传动系统的扭矩轴要求较好的稳健性[2],张丹等[3]通过优化参数改善其动态特性。针对截割部传动齿轮,提高传动机构可靠性是众多学者研究的重要方向。吴卫东等[4]建立行星轮系数学优化模型,使用Isight软件进行参数优化,有效提高截割部行星机构各齿轮的弯曲强度。赵丽娟等[5]以多体动力学理论研究行星轮系受力情况,针对应力集中位置改进设计参数,提高行星机构各零部件强度。秦仙蓉等[6]根据拟合分目标函数关系完成行星机构的多目标优化,在重量更轻的情况下,有效提高可靠度和传动特性。张利等[7]使用KISSsoft建立采煤机行星传动机构的参数化模型,以弯曲疲劳和接触疲劳的安全系数为目标进行优化,有效提高了行星机构的可靠性。
笔者以某型采煤机截割部行星机构为例,通过选择齿数、模数和变位系数为设计变量,建立以弯曲应力和各齿轮总体积为目标的优化模型,考虑行星机构优化模型的非线性多峰特性,引入烟花算法[8](FWA),改进传统烟花算法,求解优化模型。
1 数学模型的建立1.1 设计变量的选取采煤机行星传动机构多采用角变位齿轮,考虑优化目标和约束条件,选择太阳轮、行星轮和内齿圈的齿数za、zb、zc、模数m、变位系数xa、xb、xc7个齿设计变量为
X=(za,zc,zb,m,xa,xb,xc)T。
1.2 目标函数的确定某采煤机截割部装机功率250 kW,是单级NGW型行星机构,其太阳轮转速为220 r/min,行星轮个数K=4,以齿根弯曲承载能力函数为目标[9]
σF=(Ft)/(bm)YFaYSaYεYβKAKVKFβKFα,
式中:KA——使用系数,文中取2;
KV——动载系数,文中取1.035;
KFβ——齿向载荷分布系数,文中取1.204;
KFα——齿间载荷分布系数,文中取1;
Yε——弯曲强度重合度系数,Yε=0.25+0.75/ε;
ε——对应齿轮对的重合度;
YFa——齿形系数;
YSa——应力修正系数;
Yβ——螺旋角系数,文中取1。
行星轮弯曲应力目标函数为
f1(x)=(519 120)/(zabm2)(0.25+0.75/εac),
式中,εac、εcb——对应齿轮的齿面重合度。
每个齿轮体积以节圆和齿宽组成的圆柱体体积等效代替,行星机构体积目标函数为
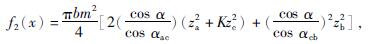
式中:α——齿顶圆压力角;
αac、αcb——对应轮组啮合角。
对于多目标优化问题,为使所有目标处于一个量级,归一化原目标函数,在求解过程中获得更多Pareto解集,设置动态权重[10]为
F(x)=w1 fc f1(x)+w2 fv f2(x),
式中,fc、fv——目标函数原始值的倒数。
设t为当前迭代数,f为权重循环频率,w1、w2为动态权重,计算公式为
w1(t)=|sin(2πt/f)|,
w2(t)=1-w1(t)。
1.3 约束条件的确定(1)传动比约束
为保证工作性能,优化后按照传动比的误差不得大于10%,可得
g1=|(1+zb/za)-5.06|-0.5≤0。
(2)重合度约束
g2=1.2-1/(2π)[za(tan αa-tan αac)+ zc(tan αc-tan αac)]≤0,
g3=1.2-1/(2π)[zc(tan αc-tan αcb)- zb(tan αb-tan αcb)]≤0。
式中,αa、αc、αb——对应的齿顶圆压力角,rad。
(3)齿顶厚约束
g4=0.25m-(mza+2m(1+xa-Δy))·((π)/(2z)a+(2xa)/(za)tan α+inv α-inv αa)≤0,
g5=0.25m-(mzc+2m(1+xc-Δy))·((π)/(2zc)+(2xc)/(zc)tan α+inv α-inv αc)≤0,
g6=0.25m-(mzb-2m(1-xb-Δy))·((π)/(2zb)-(2xb)/(zb)tan α-inv α+inv αb)≤0,
式中,Δy——齿顶高变动系数。
(4)齿轮过渡曲线干涉约束
g7=(zc)/(za)(tan αc-tan αac)-tan αac+tan α-(4(1-xa))/(zasin 2α)≤0,
g8=(za)/(zc)(tan αa-tan αac-tan αac+tanα-(4(1-xc))/(zcsin 2α)≤0。
(5)齿面接触强度约束
太阳轮与行星轮的材料均为18Cr2Ni4WA,其接触疲劳极限σHlim=1 600 MPa,内齿圈材料为42CrMo,其接触疲劳极限为σHlimb=1 000 MPa。齿面接触强度许用应力为σHP=0.95σHlim,接触应力计算式为
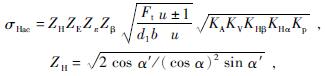
式中:ZH——节点区域系数;
Zε——重合度系数,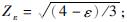
ZE——弹性系数,文中取值为189.812 N/MPa;
Zβ——螺旋角系数,文中取1;
u——齿数比。
对应的太阳轮与行星轮、行星轮与内齿圈的接触应力约束为
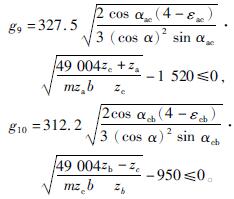
(6)行星齿轮的领接条件约束
g11=zc+2(1+xc)-(za+zc)sin(π)/4<0。
(7)齿轮的无侧隙啮合
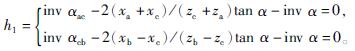
(8)行星轮系同心条件
h2=(za+zc)/(cos αac)-(zb-zc)/(cos αcb)=0。
(9)装配条件
h3=(za+zc)/4=C,
式中,C——任意整数。
2 改进的烟花算法2.1 烟花算法FWA以模拟烟花爆炸作为随机探索机制,在选择策略中平衡适应度在与个体在种群中聚集情况,使烟花算法构建一种平衡局部探索和全局探索资源分配的方式,各算子具体运行方式如下。
(1)种群的初始化
设xi=(xi1,xi2,…,xij,…,xiD)为第i个烟花的当前位置,其表达式为
xi=(xmax-xmin)rand(1,D)+xmin,
式中:M——种群规模;
D——变量维度;
xij——第i个烟花j个维度上的分量。
(2)爆炸火花的范围和数量
设烟花位置为xi,则其子代数量Si以及爆炸半径Ai计算方式为
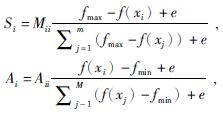
式中:Mii、Aii——调节数量、爆炸半径;
fmax、fmin——f(xi)的适应度最大值、最小值;
e——定义的极小量。
设置每个子代火花的数量范围,进行约束为
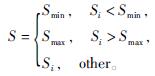
(3)子代火花生成
在烟花xi上随机选择更新z维的位置信息,对所选z维的xki进行位置偏移形成新的xki。根据上述烟花的爆炸范围给新xki进行位移,表达式为
xik=xik+hk,
hk=Airand(-1,1)。
(4)高斯变异火花
烟花算法通过在子代火花中随机选取火花进行高斯变异方式跳出局部最优解,变异公式为
xkj=xkiGaussian(1,1)。
对超出许可领域的火花根据公式更新位置信息为
xjk=xmink+rand(0,1)(xkmax-xkmin)。
(5)迭代选择方式
采用轮盘赌的方式选择其他的个体,筛选概率为
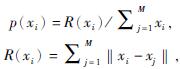
式中,R(xi)——除xi外所有个体欧式距离之和。
2.2 改进策略结合烟花算法的执行流程,活跃型烟花算法(Activation fireworks algorithm,AFWA),流程如图1所示。
(1)自适应爆炸范围
为提高算法在迭代初期的全局寻优和末期的精细化探索,使用Sigmoid函数构建火花半径的变化函数,爆炸范围条件函数为
at=1/(1+et/T·n1)+n2,
式中:n1、n2——自定义调节系数;
T——总迭代次数;
t——当前迭代次数。
新的爆炸半径函数为

(2)学习算子
针对火花间缺乏信息交流的问题,引入粒子群算法的学习方式,引导其余火花向目前最优方向进行探索,具体构造方式为
Δx=xi+cφ(k)(gbest(xi)-xi),
式中:φ(k)——随机选择的维度;
c——自定义学习因子。
3 算法仿真测试3.1 标准函数的测试为验证改进算法性能,选择Sphere、Schwefel、Rosenbrock、Ackley、Griewank和Rastrigrin共6种典型测试函数[8]进行验证。以Matlab2019版作为运行平台编译,FWA的参数设置种群规模为20,其它见文献[8],AFWA算法调节系数分别取6和0.4,学习因子为1.45,其他参数与FWA相同。所有函数问题维度均为30,迭代1 000代,寻优曲线部分见图2。
由图2和表1可以看出,AFWA相对于传统FWA表现出显著的优越性。在f1~f3函数中,最终求解的最优值、方差和平均值除Sphere函数外均优于原始算法,f4~f6函数中,从图2可以看出,改进后的算法寻优速度更快。
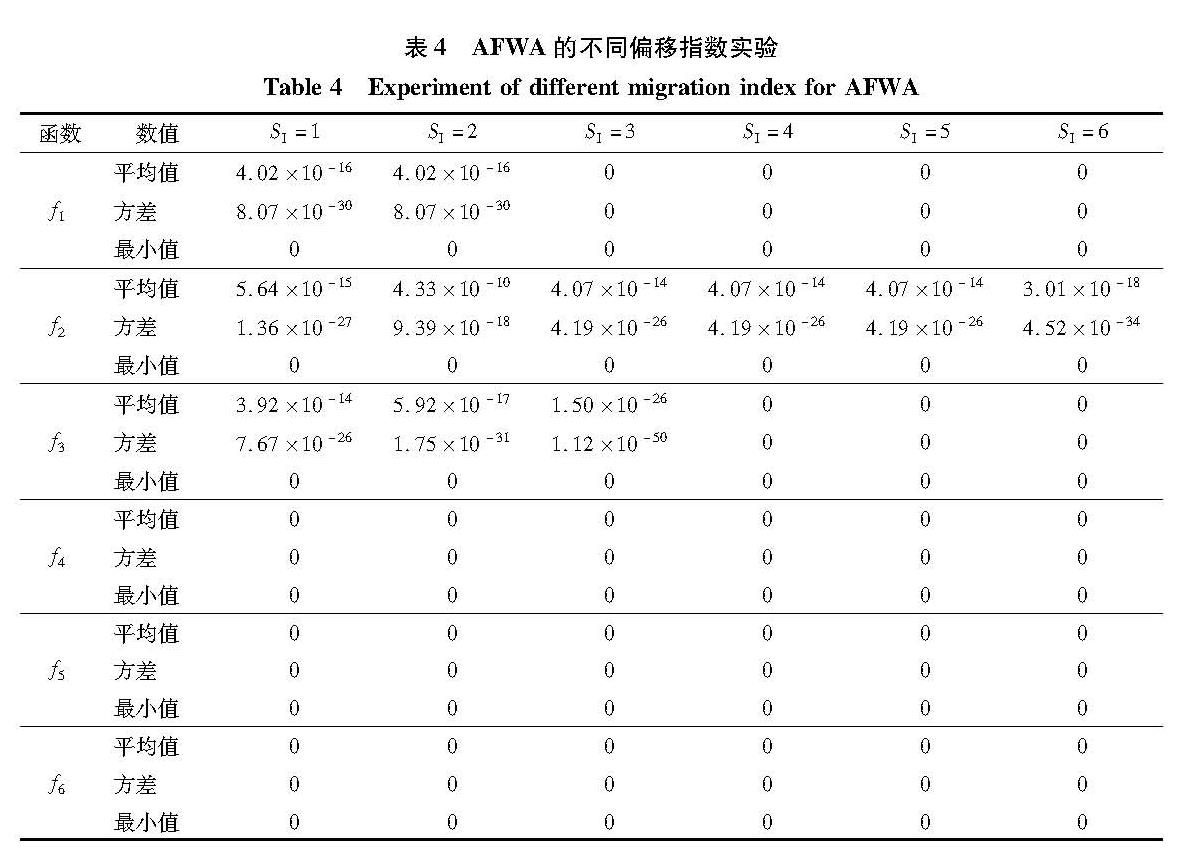
3.2 偏移函数测试在对于FWA的研究过程中,发现FWA在寻优过程中对最优解的位置有明显的敏感性,通过偏移函数最优解的位置,使最优位置不在原点或其附近时,则FWA的求解结果会变的很差[11-12]。
为检测改进算法对于偏移函数的寻优能力,给出如表2所示的偏移指数SI,设UL为函数的边界差值,偏移距离Sv使被测函数的最优点位置远离搜索区域原始位置,而测试函数的变量搜索范围不发生改变。
偏移函数测试AFWA与FWA算法,将6种典型测试函数进行6次偏移,每个偏移度的函数都计算50次,记录其最优值、平均值和方差。测试结果在图3中展示部分,详细数据如表3所示。
综上所述,通过图3和表3的对比,改进后的算法几乎不受原点偏移的影响。实验结果表明,改进后的AFWA算法不仅具有较好的稳定性和跳出局部最优的能力,且在收敛速度和精度上也有明显提高,可以应用于求解多峰特性的行星机构优化模型。
4 优化模型的求解求解行星机构优化模型为典型的混合离散函数问题[13],为使烟花算法能够求解混合离散模型,在齿数变量的寻优变化时进行圆整处理,将模数建立为数组,使用位置序号为变量参与寻优。为获得多目标问题Pareto解集,通过动态权重在不同方向上探索,将每次迭代的寻优结果进行非支配排序,以支配等级最高的个体组成新的父本火花参与下一次迭代,存储每次迭代过程中寻到的Pareto解,后进行非支配排序获得最终前沿,得到如图4中Pareto前沿。
在符合原始结构条件下,选择弯曲强度最高的优化结果如表5和6所示。
5 结 论
(1)通过Sigmoid自适应函数和学习算子,有效提高烟花算法的寻优性能并和稳健性。实验结果证明,AFWA在6种测试函数上的寻优性能与传统烟花算法相比是有着明显的优势。
(2)应用改进后的算法优化行星机构多目标,并设置动态权重分配,使得目标权重分配合理并获得较好pareto前沿,总体积降低0.95%,太阳轮弯曲应力减小15.9%、内齿圈弯曲应力减小16.7%,行星轮弯曲应力减小15.8%,优化后齿轮承载能力显著提高。
- [1] 刘春生, 白云锋, 沈佳兴. 基于HHT和排列熵的轴向倾斜截齿截割载荷特性[J]. 黑龙江科技大学学报, 2021, 31(3): 309- 317.
- [2] 吴卫东, 郭昌利. 采煤机扭矩轴卸载槽表面粗糙度的稳健特性[J]. 黑龙江科技大学学报, 2017, 27(2): 104- 108.
- [3] 张 丹, 刘春生, 王爱芳, 等. 分布质量模型下的采煤机牵引部扭振系统动态特性及优化[J]. 黑龙江科技大学学报, 2017, 27(2): 109- 113.
- [4] 吴卫东, 李君华, 薛红锐. 基于Isight采煤机截割部行星传动优化设计[J]. 煤矿机械, 2013, 34(10): 9- 11.
- [5] 赵丽娟, 乔美娜, 兰金宝. 新型采煤机截割部行星轮系强度分析[J]. 机械传动, 2015, 39(2): 107-110.
- [6] 秦仙蓉, 余传强, 孙远韬, 等. 重型顶升器行星传动系统优化设计[J]. 机械设计与研究, 2018, 34(4): 74-77.
- [7] 张 利, 黄筱调, 金 伟, 等. 基于KISSsoft的采煤机齿轮箱参数优化设计[J]. 机械设计与制造, 2020(2): 214- 217.
- [8] Tan Y, Zhu Y. Fireworks algorithm for optimization [C]. international conference on swarm intelligence, 2010: 355- 364.
- [9] 成大先. 机械设计手册[M]. 北京: 化学工业出版社, 2017.
- [10] 傅武军, 朱昌明, 叶庆泰. Multi-objectie integrated optimization based on evolutionary strategy with a dynamic[J]. Journal of Southeast University, 2006(2): 204- 207.
- [11] 余冬华, 郭茂祖, 刘晓燕, 等. 改进选择策略的烟花算法[J]. 控制与决策, 2020, 35(2): 389- 395.
- [12] 张水平, 李殷俊, 高 栋, 等. 带有动态爆炸半径的增强型烟花算法[J]. 计算机工程与应用, 2020, 56(18): 50- 57.
- [13] 王 盛, 龚宪生. 基于遗传算法的行星轮系混合离散变量优化[J]. 机械科学与技术, 2014, 33(8): 1150- 1154.
 图 1 改进烟花算法的流程
Fig.1 Flow of improved fireworks algorithm
图 1 改进烟花算法的流程
Fig.1 Flow of improved fireworks algorithm


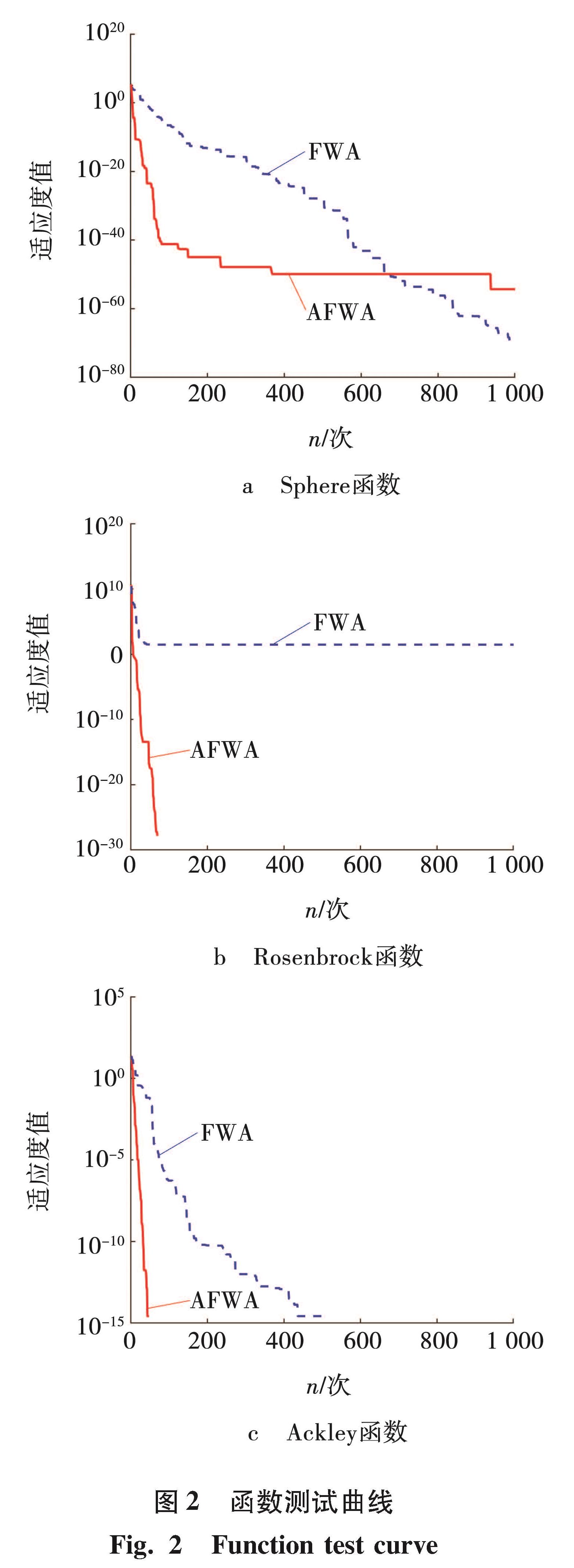 表1。"/>
表1。"/>