高性能的截割煤岩刀具是煤矿机械装备的基础,刀具截割煤岩力学模型是设计高性能刀具的关键。目前,国内外学者对刀具破碎不同强度的煤岩进行了诸多研究,如Nishimatsu[1]指出刀具破碎煤岩时,煤岩破碎面服从Mohr-Coulomb准则。梁宇等[2]通过煤岩剪切强度率效应力学特性实验,得出在不同剪切速率下煤岩的力学特性。刘晓辉等[3]根据煤岩的单轴与三轴压缩实验,研究不同围压下煤岩的强度及变形特征。Tiryaki[4]指出截齿截割比能耗与岩石抗拉强度存在线性关系。Bilgrin等[5]对不同抗压强度的岩石进行切削深度和刀具间距值的全尺寸线性实验,得出锥形刀具破岩过程中主要影响参数。周强等[6]以煤岩的颗粒破碎过程的最大破碎力和断裂能,探究适合煤岩颗粒强度分布的数学模型。张慧梅等[7]根据岩石内部裂隙和孔隙分布的随机性,建立基于Weibull统计分布的岩石损伤模型。蒋维等[8]基于Mohr强度理论,提出服从对数正态分布建立的岩石损伤模型。岳洋[9]假定岩石微元强度服从幂函数分布,建立了岩石破坏过程中的损伤统计本构模型。Ranman[10]通过对岩石切削实验,获得了圆锥截齿破碎岩石过程的载荷变化特征。张桂菊等[11-12]通过对TBM盘型滚刀的研究,构建了盘型滚刀破岩的力学模型。林敏等[13]针对硬地层的工况,提出类盘式牙轮式钻头破岩机理。Muro等[14]揭示了点冲击钻头破碎岩石的机理。刘春生等[15-21]提出一种以轴向振动与径向切削运动形式破碎煤岩的新型刀具,研究了其破岩机理和载荷特性。笔者通过分析碟盘刀具振动切削煤岩的力学过程,引入煤岩的损伤统计理论,建立碟盘刀具破碎煤岩的理论模型,采用ABAQUS 有限元仿真软件模拟碟盘刀具破碎煤岩过程,通过碟盘刀具复合振动切削破碎煤岩的仿真,与煤岩微元强度服从Weibull与对数正态分布建立理论模型计算结果进行对比,验证模型的适用性。
1 煤岩破碎力学模型碟盘刀具是一种新型破碎煤岩的刀具,由刀刃和楔面两部分组成,其结构如图1所示。以轴向振动vs与径向切削vj的运动方式破碎煤岩,刀刃有助于刀具楔入煤岩,楔面部分则有助于煤岩的大块崩落。
碟盘刀具破碎煤岩的过程中,煤岩在碟盘刀具轴向振动作用下发生损伤,随着碟盘刀具对煤岩的径向切削作用,煤岩在刀具楔面施加载荷下发生剪切破坏,当剪切破碎面上的力达到煤岩剪切强度时,剪切破碎面上的煤岩发生大块崩落即煤岩从岩体上滑移分离。碟盘刀具振动切削破碎煤岩过程中,假设煤岩破碎服从Mohr-Coulomb准则,破碎形式为剪切破坏,选取碟盘刀具等效单元分析破碎煤岩过程中的受力,煤岩在剪切破碎面上存在与剪切破碎面平行的剪切破碎力FS和相反方向抵抗剪切破碎力FR,如图2所示。
由图2可见,剪切破碎面平行的剪切破碎力为
FS=τnBlcos β。(1)
相反方向抵抗剪切破碎力为
FR=(μσn+c)Blcos β,(2)
式中:μ——内摩擦系数,μ=tan φ;
φ——内摩擦角;
c——内聚力,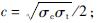
σc——抗压强度;
σt——抗拉强度,σt=(0.03~0.1)σc;
l——煤岩破碎面中心剪切破碎线长度,l=h/sin ψ;
ψ——煤岩崩落角;
B——刀具刀刃与煤岩接触弧长,文中取单位长度1 mm;
τn——煤岩剪切破碎线上外部施加的剪切应力;
σn——煤岩剪切破碎线上外部施加的正应力;
β——煤岩剪切破碎面中心破碎线与两侧破碎线的夹角,文中β取0°~90°。
根据图2的受力分析可得,碟盘刀具单位长度对应的楔面部分破碎煤岩所受的总载荷为
Fz=1/(cos ξ)(FS-FR)=1/(cos ξ)FH,(3)
式中:ξ——碟盘刀具楔面作用合力与煤岩剪切破碎面的夹角,ξ=90°-α-ψ,
α——碟盘刀具楔面角。
根据碟盘刀具单位长度对应的楔面部分破碎煤岩所受的总载荷,可以得其径向载荷为
Faj=Fzcos ω,(4)
式中,ω——碟盘刀具总载荷与径向载荷间夹角,ω=ψ+ξ。
碟盘刀具在破碎煤岩过程中,有效截割面积为刀具的1/2,刀盘半径为125mm,且载荷从刀刃中间向两侧逐级递减,即可得碟盘刀具破碎煤岩径向载荷为

在煤岩破碎过程中,基于Mohr-Coulomb准则可得剪切破碎面上的正应力为
σ*n=1/2(σ1+σ3)+1/2(σ1-σ3)cos 2θ,(6)
剪应力为
τ*n=1/2(σ1-σ3)sin 2θ,(7)
式中:σ1——第一主应力;
σ3——第三主应力;
θ——剪切面的法线方向与第一主应力σ1的夹角。
2 不同损伤统计分布下的力学模型考虑碟盘刀具轴向振动对煤岩的损伤作用,引入统计损伤理论,假设碟盘刀具轴向振动时煤岩内部损伤服从某种分布,在碟盘刀具破碎煤岩的过程中,煤岩符合Lemaitre提出的应变等价性假说,煤岩损伤的本构关系为
σ=σ*(1-D)=Eε(1-D),(8)
式中:σ——煤岩外部施加应力;
σ*——煤岩内部有效应力;
D——损伤变量;
E——弹性模量;
ε——应变。
假定煤岩微元在破碎前,服从虎克定律,根据式(8)可得
D=1-(σ1)/(Eε1),(9)
式中,ε1——主应力作用下的应变。
由式(8)可以得出,在煤岩剪切破碎面上的外部施加正压力σn和剪切力τn为
σn=σ*n(1-D),(10)
τn=τ*n(1-D)。(11)
由式(10)、(11)可知,要准确表达煤岩破碎过程中的有效剪应力和有效正应力,关键要求得煤岩的损伤变量D。损伤变量D为某一荷载作用下已破坏的微元数目n与总微元数N的比值,用于衡量岩石损伤程度的大小。在碟盘刀具振动损伤破碎煤岩的过程中,煤岩的破坏为损伤积累的过程,损伤变量为

式中:F——煤岩微元强度;
P(x)——煤岩微元概率模型。
煤岩在破碎过程中服从Mohr-Coulomb准则,根据Mohr-Coulomb准则主应力公式,可得煤岩微元强度为
F=1/2(σ1-σ3)+1/2(σ1+σ3)sin φ。(13)
煤岩微元概率模型是假设碟盘振动损伤煤岩在破碎过程中内部损伤服从某种概率模型,文中采用Weibull分布和对数正态分布构建碟盘刀具破碎煤岩的损伤力学模型。
2.1 Weibull分布假设碟盘刀具振动切破碎削煤岩过程中,其内部损伤服从的Weibull分布
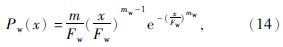
式中:x——微元强度的随机分布变量;
mw、Fw——Weibull分布参数。
将式(14)代入式(12),可得服从Weibull分布概率下的煤岩损伤变量为

将服从Weibull分布概率模型下的煤岩损伤变量代入式(5),因σ3相对较小,故仅考虑σ1,可得碟盘刀具破碎煤岩的力学模型为
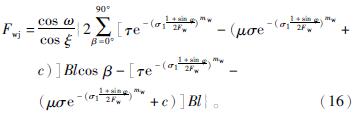
结合式(9)、(15),取两次对数可得
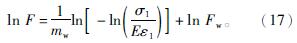
假设碟盘刀具振动切削破碎煤岩过程中内部损伤服从的对数正态分布为
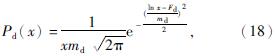
式中:x——微元强度的随机分布变量;
md、Fd——对数正态分布参数。
与Weibull分布计算步骤相同,可得服从的对数正态分布概率模型下的煤岩损伤变量和碟盘刀具破碎煤岩的力学模型分别为
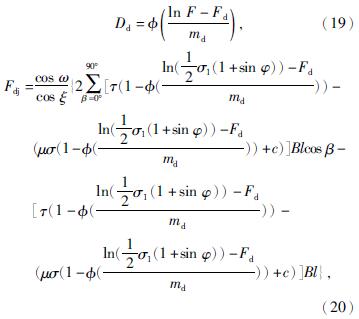
式中,φ((ln F-Fd)/(md))——标准正态分布函数。
将式(9)移项代入式(19)可得
Dd=1-(σ1)/(Eε1)=Φ((ln F-Fd)/(md)),(21)
令Φ(X)=1-(σ1)/(Eε1),可得
ln F=mdX+Fd。(22)
2.3 分布参数的确定为确定各微元概率模型分布参数,对19、33、75、94 MPa强度的煤岩进行单轴抗压实验,得出不同强度煤岩下的应力与应变参数,设定碟盘刀具切削煤岩厚度为14 mm,将其代入式(17)、(22)并线性拟合可得,Weibull分布参数mw、Fw,对数正态分布参数md、Fd,如表1所示。
2.4 理论载荷
将各微元概率模型分布参数、不同强度的煤岩参数和碟盘刀具参数代入式(16)、(20),可得基于Weibull分布、对数正态分布两种分布建立的力学模型计算的碟盘刀具所受的径向载荷,如表2所示。
3 碟盘刀具复合破碎煤岩的仿真
为了验证基于不同损伤统计本构模型建立的碟盘刀具破碎煤岩力学模型的准确性,选用最佳的损伤统计本构模型建立的碟盘刀具破碎煤岩力学模型,采用ABAQUS 有限元仿真软件对碟盘刀具破碎煤岩的过程进行仿真。刀具和煤岩体都采用六面体C3D8R的单元,煤岩采用Drucker-Prager塑性本构模型。选取工况进行仿真,其刀具楔面角α为50°、切削厚度h为14 mm、进给速度vj为300 mm/s、振动幅值A为2.0 mm、振动频率f为45 Hz。
在ABAQUS 有限元仿真软件中对碟盘刀具破碎煤岩建立模型,如图3所示。根据19、33、75、94 MPa四种强度的煤岩破碎的仿真,可以得到仿真结果的径向载荷如图4所示。
根据仿真结果求取碟盘刀具破碎不同强度煤岩的径向载荷均值,在19、33、75、94 MPa强度的煤岩下,碟盘刀具所受的径向载荷均值分别为14.64、37.65、80.04、117.77 kN。
在19、33、75、94 MPa强度下,碟盘刀具振动切削煤岩大块崩落阶段的应力云图,如图5所示。由图5可知,碟盘刀具破碎煤岩时,应力损伤面积从中间向两侧逐渐减小,破碎煤岩形状呈月牙状,破碎面积从中间向两侧逐渐递减; 其应力延伸扩展变化也呈月牙状,应力面积从中间向两侧递减,说明计算碟盘刀具径向总载荷的理论模型推论符合实际。碟盘刀具在破碎不同强度煤岩的过程中,随着煤岩强度增加,在相同结构参数与运动参数下,刀具所受的径向载荷明显增大,符合理论模型的计算结果即随着煤岩强度增大径向载荷不断增大。
在破碎不同强度煤岩时,基于Weibull分布和对数正态分布所建立的载荷模型的理论值与仿真结果值具有相对较好的吻合性,基于Weibull分布和对数正态分布建立模型误差值范围分别为0.45%~3.25%和0.42%~3.42%,其平均误差值分别为2.29%、2.34%。根据平均误差值的大小、模型误差的精确性及理论分析综合考虑,基于Weibull分布、对数正态分布建立模型适用于碟盘刀具破碎煤岩的分析。
4 结 论
(1)通过分析碟盘刀具振动切削煤岩破碎过程,引入统计损伤理论,分别给出了基于Weibull分布和对数正态分布,根据Mohr-Coulomb破坏准则建立了煤岩大块崩落的载荷模型。
(2)通过煤岩的应力与应变特性曲线,给出了Weibull和对数正态两种分布下的损伤因子,计算了两种分布下理论模型的均值,基于Weibull分布和对数正态分布建立模型的理论计算值与仿真载荷均值误差范围分别为0.45%~3.25%和0.42%~3.42%,平均误差分别为2.29%、2.34%。综合考虑分析,可得基于Weibull和对数正态分布建立的碟盘刀具复合振动切削煤岩的损伤力学模型适用碟盘刀具的载荷计算。
(3)由于理论模型采用的是Mohr-Coulomb准则,而ABAQUS 有限元中煤岩体的模型为Drucker-Prager准则,Mohr-Coulomb与Drucker-Prager准则在内聚力和内摩擦角存在一定的转换关系,文中未考虑其转换关系,在下一步的研究中,进一步构建基于Mohr-Coulomb准则理论模型与ABAQUS 有限元模型的转换关系。
- [1] Nishimatsu Y. The mechanics of rock cutting[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1972, 9(2): 261-270.
- [2] 梁 宇, 徐素国, 刘 超, 等. 不同速率下的煤岩剪切强度力学特性[J]. 煤矿安全, 2018, 49(2): 5-7.
- [3] 刘晓辉, 余 洁, 康家辉, 等. 不同围压下煤岩强度及变形特征研究[J]. 地下空间与工程学报, 2019, 15(5): 1341-1352.
- [4] Tiryaki B, Cagatay D A. Effects of rock properties on specific cutting energy in linear cutting of sandstones by picks[J]. Rock Mechanics and Rock Engineering, 2006, 39(2): 89-120.
- [5] Bilgin N, Demircin M A, Copur A, et al. Dominant rock properties affecting the performance of conical picks and the comparison of some experimental and theoretical results[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 43(1): 139-156.
- [6] 周 强, 潘永泰, 徐宏祥. 单轴压缩作用下煤岩颗粒强度分布实验研究[J]. 中国矿业大学学报, 2020, 49(2): 381-386.
- [7] 张慧梅, 雷利娜, 杨更社. 基于Weibull统计分布的岩石损伤模型[J]. 湖南科技大学学报(自然科技学版), 2014, 49(3): 29-32.
- [8] 蒋 维, 邓 建. 基于对数正态分布的岩石损伤统计分析方法研究[J]. 南华大学学报(自然科技学版), 2010, 24(2): 34-37.
- [9] 岳 洋. 岩石损伤本构模型研究[J]. 贵州大学学报(自然科技学版), 2010, 27(4): 117-119.
- [10] Ranman E. A model describing rock cutting with conical picks[J]. Rock Mechanics and Rock Engineering, 1985, 18(2): 131-140.
- [11] 张桂菊, 谭 青, 劳同炳. TBM盘形滚刀切削力学模型分析[J]. 中南大学学报(自然科技学版), 2020, 51(10): 2792-2799.
- [12] 张桂菊, 谭 青, 劳同炳. 不同动静载荷组合作用下盘形滚刀破岩机制[J]. 中南大学学报(自然科技学版), 2019, 50(3): 540-549.
- [13] 林 敏, 刘八仙, 杨迎新, 等. 类盘式牙轮钻头破岩机理实验研究[J]. 中南大学学报(自然科技学版), 2017, 40(1): 11-13.
- [14] Muro T, Takegaki Y, Yoshikawa K. Impact cutting property of rock material using a point attack bit[J]. Journal of Terramechanics, 1997, 34(2): 83-108.
- [15] 刘春生, 徐玉芸, 李德根, 等. 碟盘刀齿冲击与切削复合破碎煤岩的载荷特性[J]. 黑龙江科技大学学报, 2017, 27(2): 97-103.
- [16] 刘春生, 徐玉芸, 袁 昊, 等. 碟盘刀具振动与切削破碎煤岩力学特性的数值模拟[J]. 黑龙江科技大学学报, 2018, 28(1): 36-42.
- [17] 刘春生, 徐玉芸, 李德根, 等. 边缘牙齿形碟盘破碎煤岩的力学机理及其模型[J]. 煤炭学报, 2018, 43(1): 272-279.
- [18] 刘春生, 袁 昊, 张艳军, 等. 不同楔面角度碟盘刀具切削煤岩的载荷与小波能量熵[J]. 黑龙江科技大学学报, 2018, 28(5): 543-551.
- [19] 刘春生, 李德根, 任春平. 基于熵权的正则化神经网络煤岩截割载荷谱预测模型[J]. 煤炭学报, 2020, 45(1): 474-483.
- [20] 刘春生, 刘延婷, 徐玉芸, 等. 碟盘刀具上刀齿切削煤岩的载荷特性研究[J]. 煤炭科学技术, 2019, 47(7): 176-182.
- [21] 刘春生, 袁 昊, 李德根, 等. 碟盘刀具轴向振动破碎煤岩载荷模拟与粉碎量研究[J]. 煤炭科学技术, 2020, 48(1): 189-195.
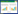 图 1 碟盘刀具
Fig.1 Disc cutter
图 1 碟盘刀具
Fig.1 Disc cutter







