行走机构承担采煤机沿工作面导向槽行走的任务,随着对采煤机工作性能要求的不断提高,其装机功率和牵引力也随之增大,行走轮经常发生过度磨损,严重时甚至断齿[1-2]。针对行走轮的力学特性,国内外学者开展了大量研究,黑龙江科技大学研究团队探究了行走系统刚度对齿销啮合力的影响,分析了行走轮与销排的极限啮合工况,设计了一种采煤机液压浮动支撑自适应调姿牵引机构,有效降低牵引速度波动。张丹等[3-5]研究了摆线齿廓行走轮齿销啮合特性,得到了销排过渡处牵引速度和加速度变化规律。相关学者从外部载荷特性入手,分析了瞬时冲击、短时过载工况对齿销啮合力的影响规律[6-7],还有从截割载荷模型的构建及载荷谱的预测研究截割煤岩截荷变化特性,获得滚筒随机载荷下行走机构力学特性[8-9]。近年来,对采煤机行走部的研究多以单因素变量法为主,通过单一变量分析行走机构动力学特性,且牵引阻力由电机功率转换得到,存在较大误差。笔者在现有研究的基础上,根据截割阻力和牵引阻力匹配公式计算牵引阻力,研究节距、中心距、煤层倾角等对齿销啮合力和啮合力波动率的影响规律,通过正交实验法分析行走机构力学特性的主要影响因素。
1 行走机构动力学模型1.1 行走轮-销齿啮合力采煤机行走部销齿传动过程与齿轮齿条传动过程类似。动态激励是行走机构系统振动的根源,主要包含刚度激励、啮合冲击激励和误差激励三部分[10]。
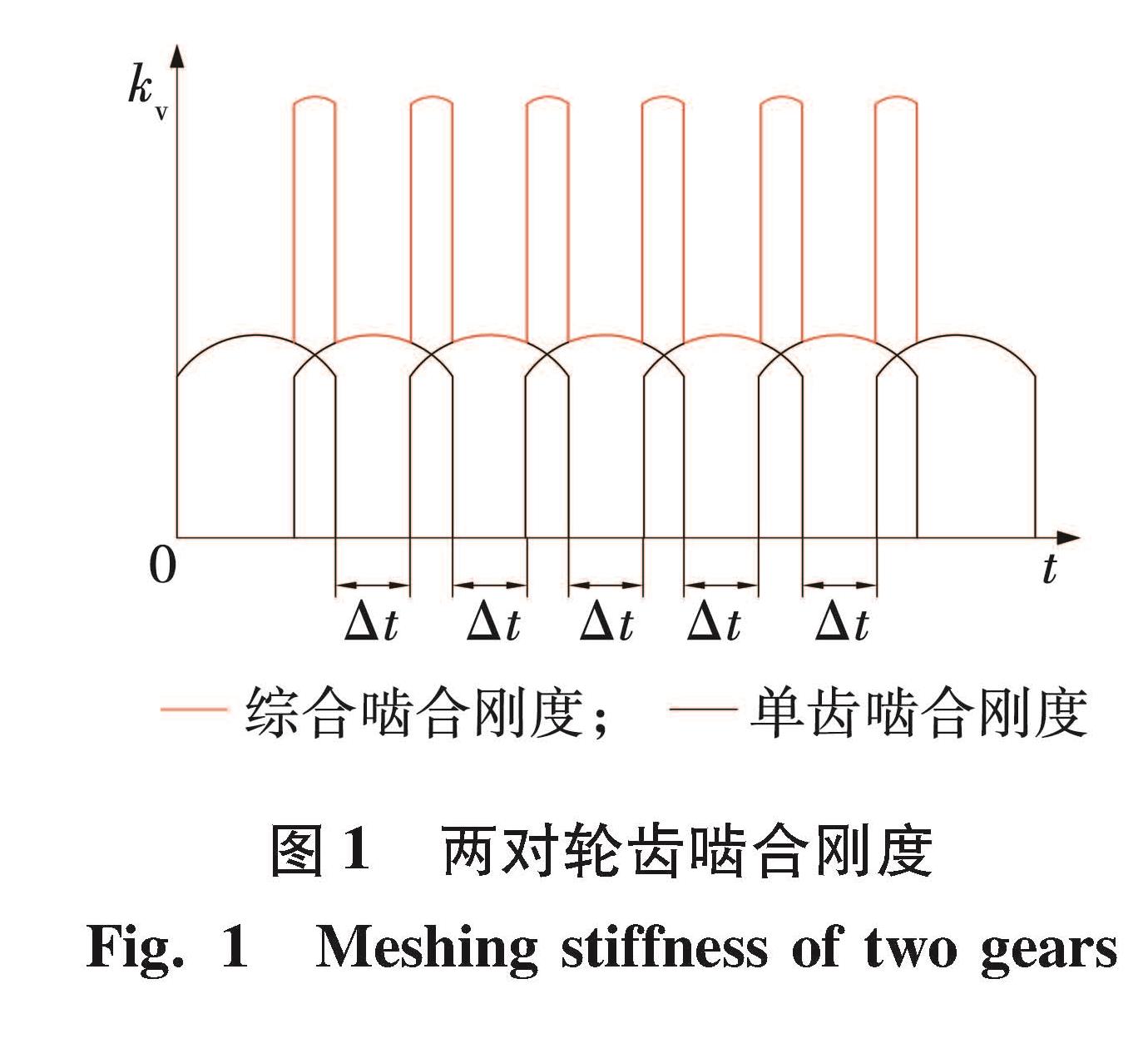
1.1.1 刚度激励牵引部传动系统各级齿轮相互啮合过程中由于重合度变化会引起刚度激励。通常情况下,销齿传动重合度1<ε<2,在啮合过程中一对齿与两对齿交替啮合,销齿传动的综合啮合刚度kv可表示为
kv=∑kvi,i=1,2,(1)
式中:kvi——第i对销齿的综合啮合刚度,kvi=k1ik2i/k1i+k2i,N/mm;
k1i——行走轮啮合点法向啮合刚度,N/mm;
k2i——销齿啮合点法向啮合刚度,N/mm。
两对销齿啮合刚度变化如图1所示,Δt为一对轮齿啮合时间,实际进行分析时用矩形波替代。
1.1.2 啮合冲击激励
行走轮制造过程中基节误差的存在和销齿啮合时的弹性变形均会导致啮合冲击,啮合冲击属于瞬间行为,是一种动态载荷激励,采用常规方法很难定量确定啮合冲击激励f(t),可通过有限元方法模拟的齿轮传动内部的啮合冲击激励近似代替。
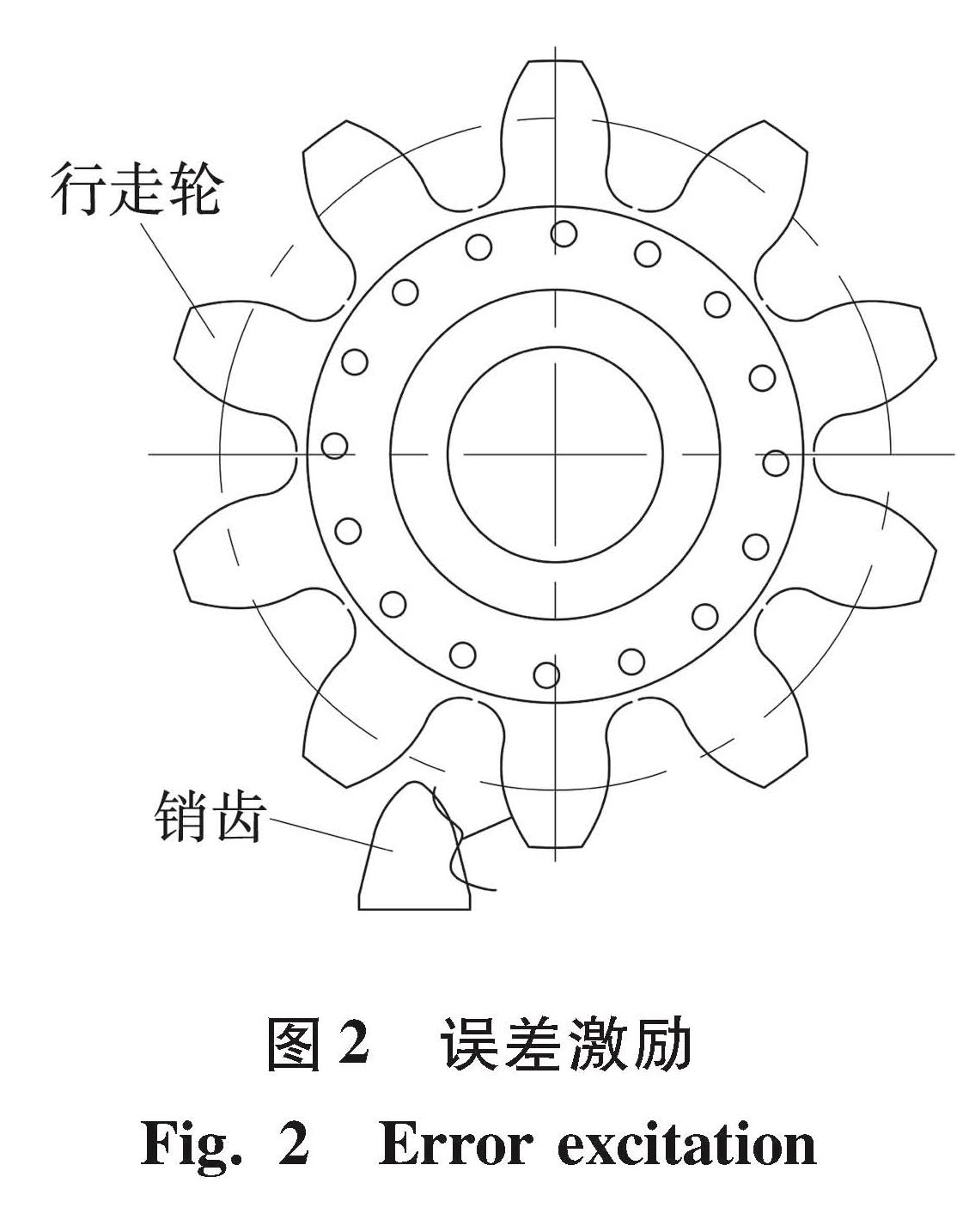
1.1.3 误差激励采煤机行走部属于开式传动,截煤过程中大量煤粉与煤块会掉落齿轨上,销齿啮合处接触精度不高,因此,误差激励不容忽视。齿销啮合过程误差激励如图2所示,与接触点处弹性变形量有关,其转角长周期误差近似为正弦曲线,短期误差可用傅里叶级数表示为
e(t)=∑ej(2πfmjt+φj),(2)
式中:ej、φj——第j阶分量的幅值和相位;
fm——啮频,Hz。
1.1.4 销齿啮合力
用ei表示第i对齿的齿廓误差,销齿啮合力可表示为
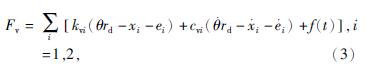
式中:θ——行走轮转角,rad;
xi——行走轮轴沿牵引方向振动位移,mm;
cvi——啮合阻尼;
rd——行走轮基圆半径,mm。
1.2 行走轮-销齿弹性碰撞模型行走轮与销排通过接触碰撞的方式传递力,impact函数定义f(d),其模拟行走轮与销排之间的接触力,f(d)函数可表示为
当d<d1时,
f(d)=k(d1-d)e-cmaxd.step(d,d1-δ,1,d1,0),
当d>d1时
f(d)=0,
式中:k——接触刚度系数,N/mm·s-1;
d1——f(d)函数阈值,mm;
d——行走轮和销齿之间距离,mm;
e——材料力指数;
cmax——阻尼系数;
δ——穿透深度,mm。
k与弹性模量和接触半径有关,可表示为
k=4/3R1/2E,
1/R=1/(R1)±1/(R2),
1/E=(1-μ21)/(E1)+(1-μ22)/(E2),
式中:E1、E2——行走轮和销排弹性模量,MPa;
R1、R2——行走轮和销排曲率半径,mm;
μ1、μ2——行走轮和销排材料泊松比。
对于行走轮与销排,其材料力指数e通常取1.5,最大穿透深度d取0.1 mm,阻尼系数cmax一般取刚度系数的0.1%~1.0%,将模型实际参数代入,求得R≈88 mm,E≈1.07×105 MPa,k≈106 mm·MPa。
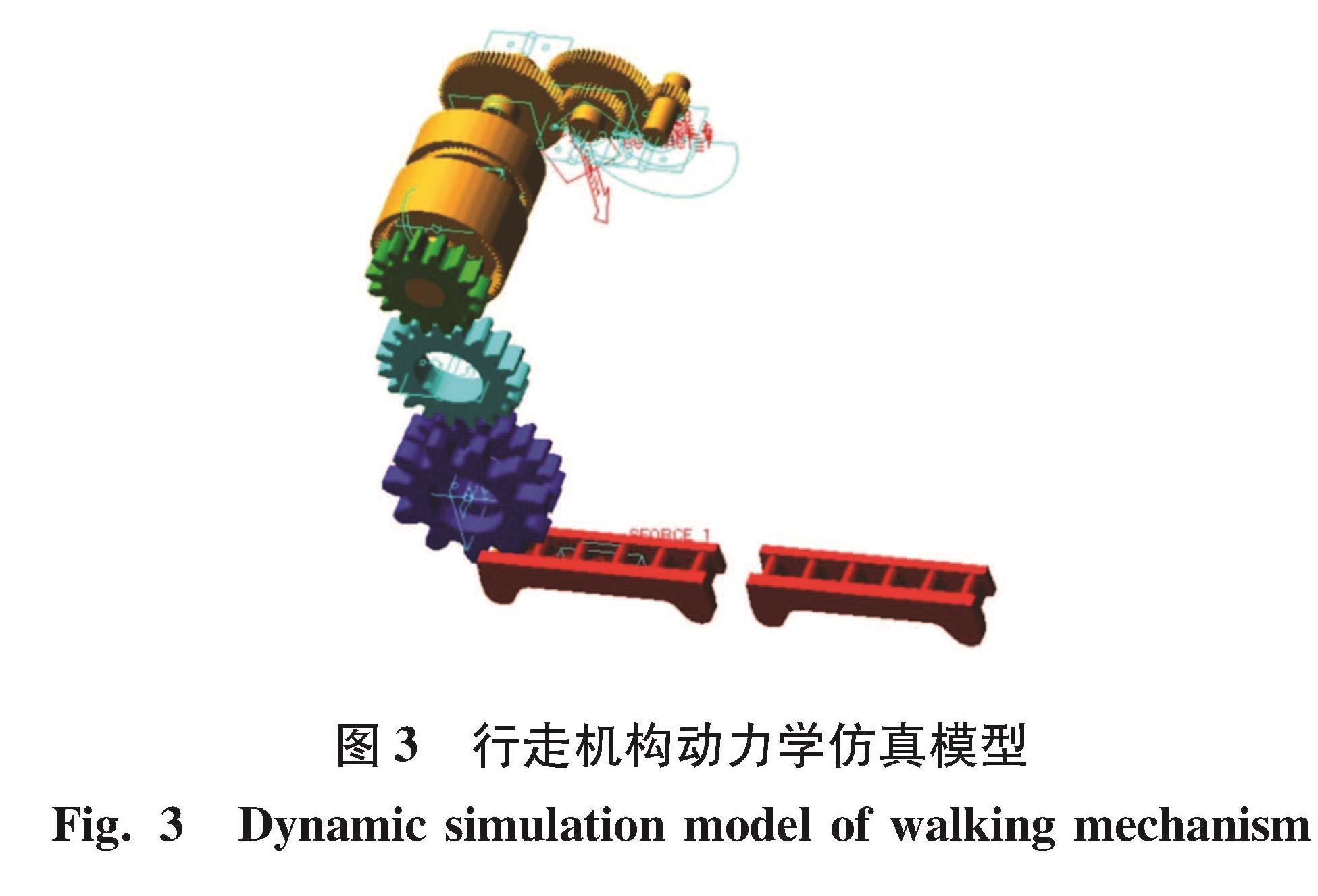
1.3 动力学仿真模型实际工况下销排固定不动,行走轮转动和向前移动,根据相对运动原理,约束行走轮定轴转动,销排只保留水平方向的移动自由度,相邻齿轮和行走轮与销排之间添加接触,齿轮与机架之间添加转动副,如图3所示。在二级减速器输入轴添加转速v=step(time,0,0,0.3,8 820d),将牵引阻力施加到销排质心处,为提高仿真精度,采用SI2求解器,仿真步长设置为0.02。
2 牵引阻力计算
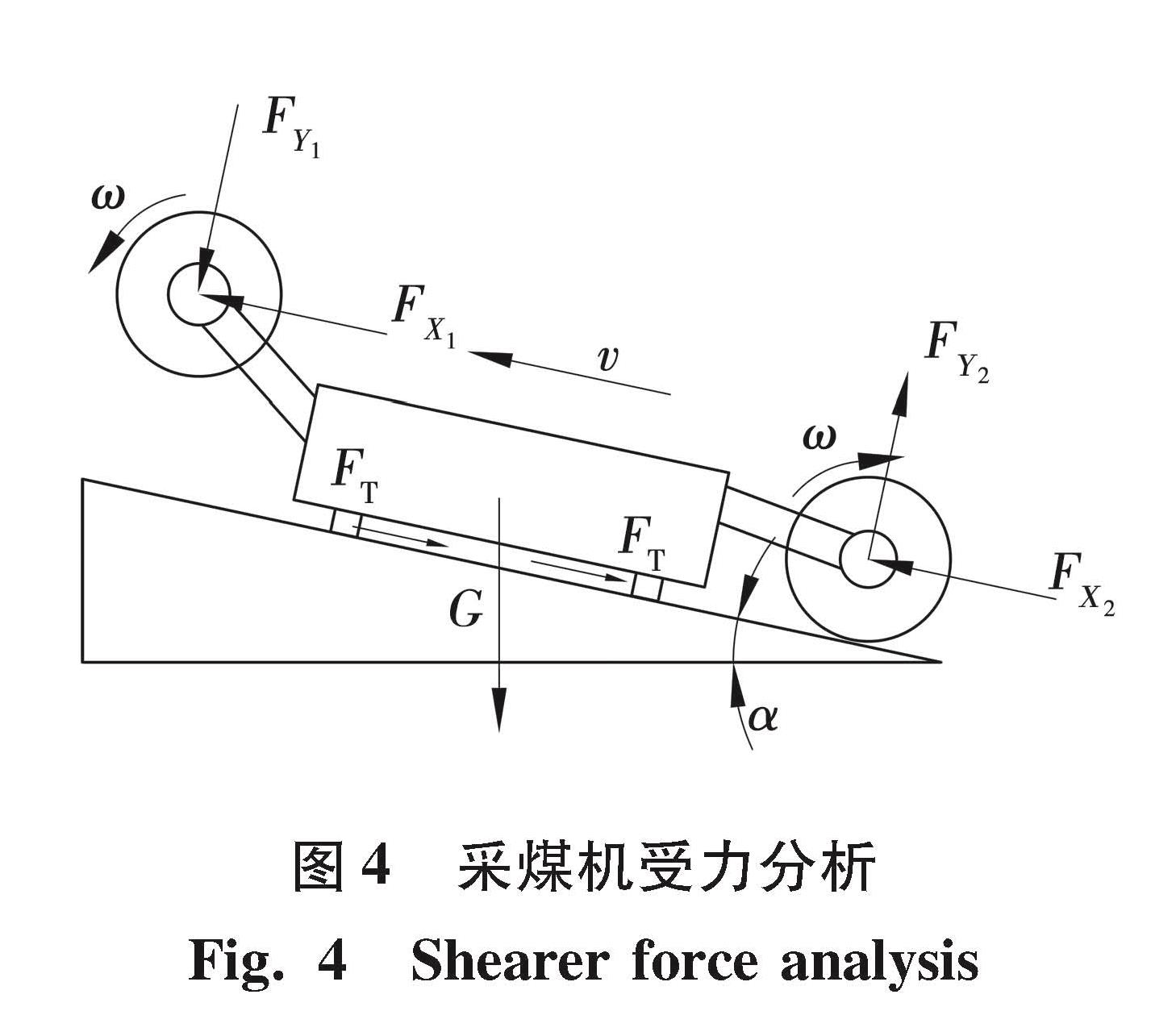
牵引阻力是设计采煤机时的重要工作参数。采煤机在工作过程中受自身重力、滚筒载荷、摩擦力和牵引力的作用,采煤机受力分析如图4所示。
牵引阻力FT可表示为
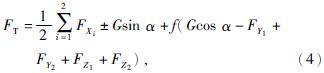
式中:FX——滚筒截割阻力,前滚筒顺转FX1为负号,后滚筒逆转FX2为正号,N;
FY——滚筒推进阻力,N;
FZ——滚筒轴向力,N;
f——滑靴与输送机轨道摩擦系数;
G——采煤机自重,N;
α——煤层倾角,(°)。
根据文献[11]计算滚筒载荷,滚筒截割阻力、推进阻力和轴向阻力可表示为
FX=(1.91×104Pjη)/(nDc),
FY=KqFX,2FZ≈(2FXbk)/J,
式中:bk——端盘部分滚筒的截割宽度,mm;
J——螺旋滚筒有效截深,mm;
k——截割条件系数,一般k=2;
Pj——截割功率,kW;
n——滚筒转速,rad/min;
Dc——滚筒直径,m;
Kq——截齿磨损系数,Kq=0.6~0.8。
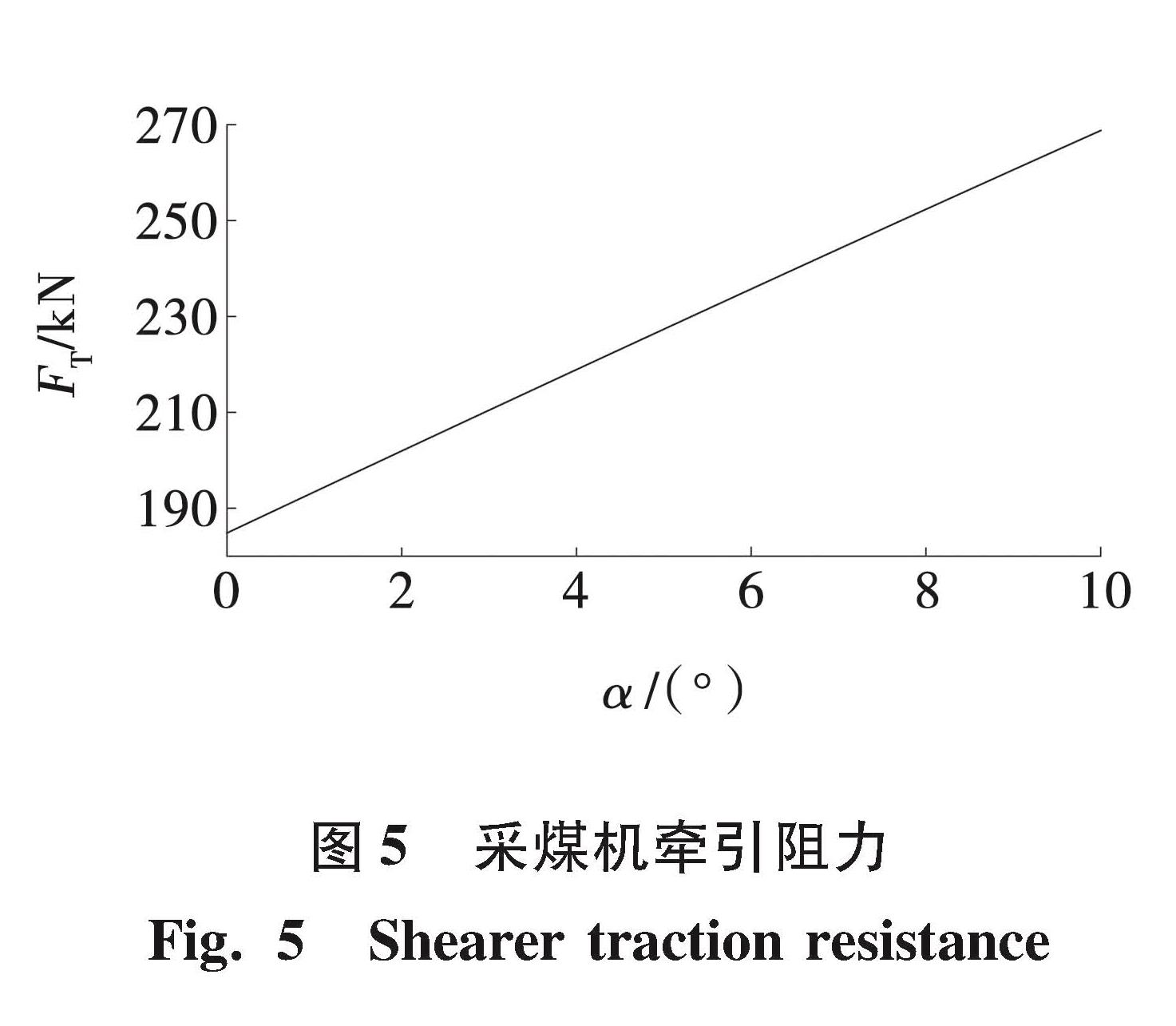
以MG650/1720型采煤机为例,采煤机基本性能参数为机重约100 t,单截割电机功率650 kW,螺旋滚筒转速30 r/min,螺旋滚筒直径2.24 m。牵引阻力与煤层倾角之间关系如图5所示。
当煤层倾角为0°时,牵引阻力约为184 kN,煤层倾角为5°时,牵引阻力约为227 kN,煤层倾角为10°时,牵引阻力约为270 kN。
3 行走机构齿销啮合特性3.1 标准工况下齿销啮合特性施加牵引阻力FT=step(time,0,0,0.3,184 000),其作用点选择销排质心处,标准工况下齿销啮合力曲线如图6所示。
在0~0.3 s内,随着电机启动齿销啮合力平缓上升,达到稳定阶段后啮合力呈周期性波动,周期约为0.88 s,波动周期与单齿啮合周期一致。行走轮与销齿圆弧段啮合时压力角大于与直线段啮合时压力角,行走轮与销齿圆弧段接触时,啮合力达到最大值228 kN,与直线段啮合时,啮合力较小,约为186 kN。行走轮与销齿圆弧段啮合属于非共轭啮合,啮合过程中压力角一直在减小,导致啮合力波动剧烈,行走轮与直线段啮合属于共轭啮合,啮合力较为平稳,一个完整的啮合周期内啮合力波动率为22.5%。
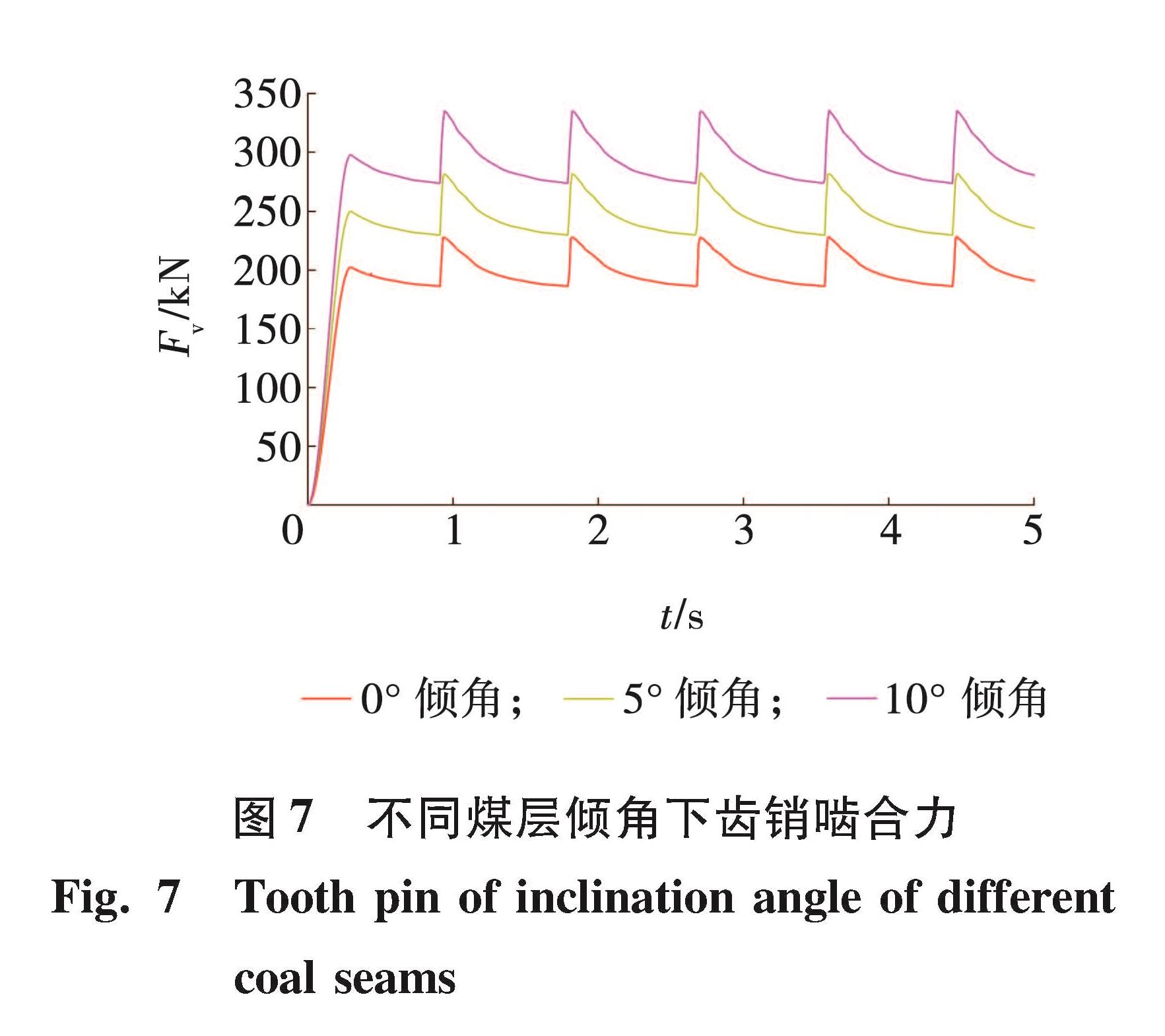
3.2 煤层倾角对齿销啮合特性的影响分别对3种不同煤层倾角工况进行仿真,不同煤层倾角下齿销啮合力曲线如图7所示。随着煤层倾角增大,齿销啮合力增大,煤层倾角由0°增大到5°时,牵引力增大了23%,啮合力幅值也增大23%; 煤层倾角由5°增大到10°时,牵引力增大了18%,啮合力幅值也增大了18%,销啮合力幅值增大的比例和牵引力增大的比例一致,不同煤层倾角下牵引力波动率也相同,均约为22.5%。
3.3 中心距对齿销啮合特性的影响
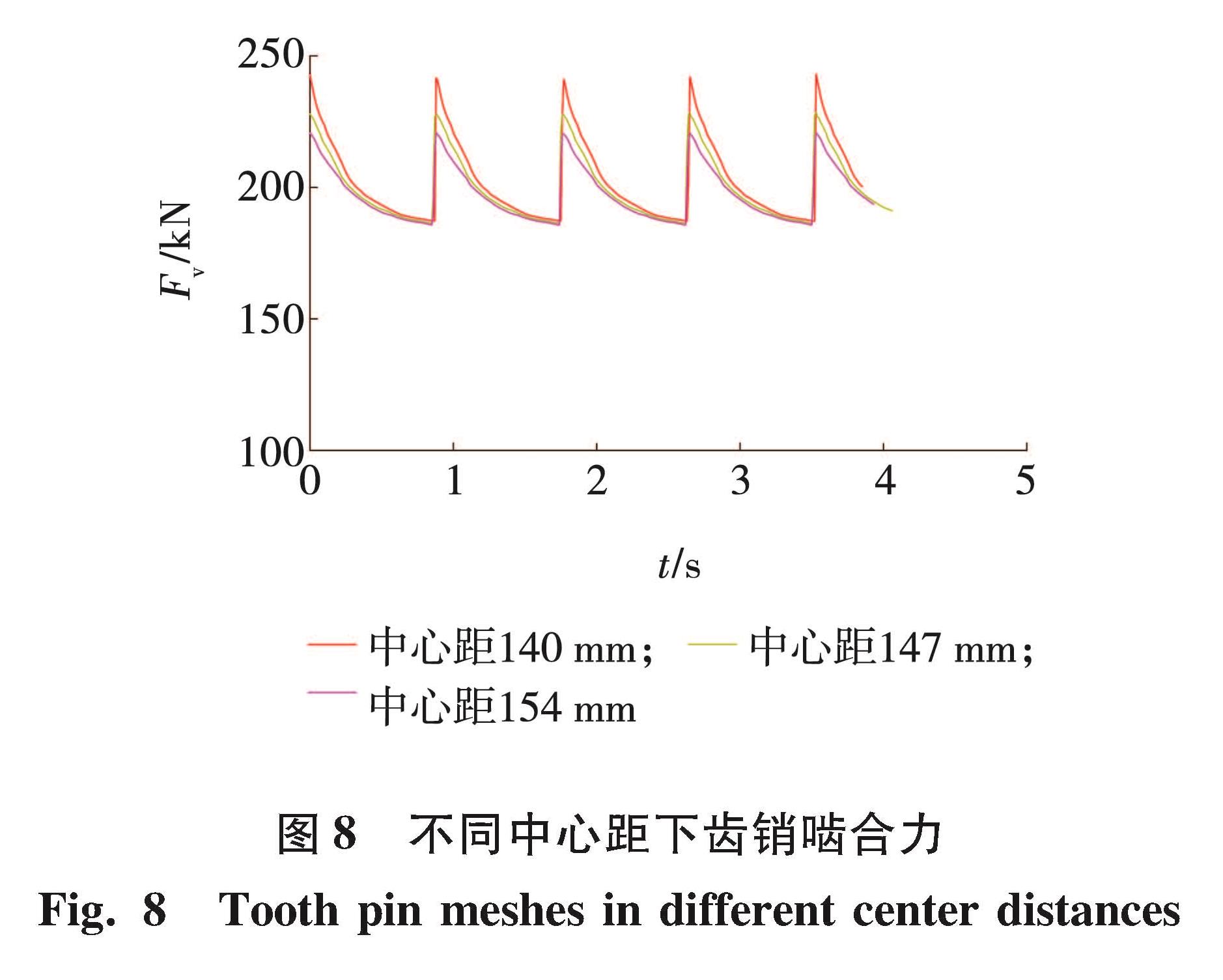
导向滑靴和销排之间留有间隙,行走轮和销排中心距在一定范围内变化,建立中心距为204 mm(最小中心距)、中心距为212 mm(标准中心距)、中心距为220 mm(最大中心距)下的动力学模型,得到不同中心距下齿销啮合力曲线如图8所示。
齿销啮合力随中心距增大而减小,最小中心距下啮合力幅值约为243 kN,标准中心距下啮合力幅值约为228 kN,最大中心距下最大啮合力幅值约为221 kN,中心距最小时,啮合力幅值比中心距最大时啮合力幅值增加了约10.1%,啮合力幅值随着中心距减小而增大,这是因为中心距减小时啮合点更靠近销排圆弧段顶部,啮合点越靠近圆弧顶部压力角越大,越不利于传动。
3.4 节距对齿销啮合特性的影响
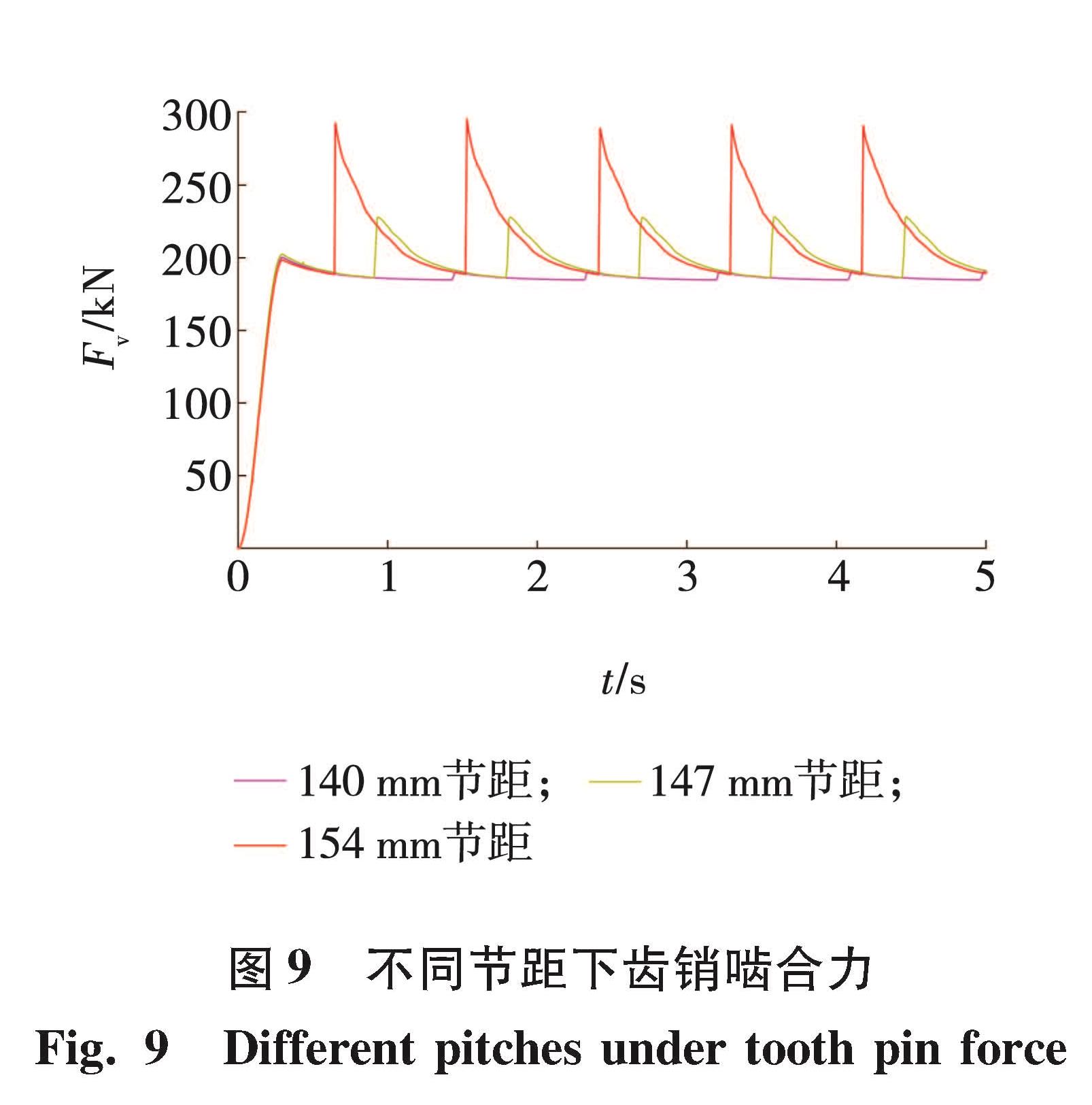
MG650/1720型采煤机与SGZ1000/1400型刮板输送机配套,所采用的Ⅲ型销排节距在140~154 mm之间变化。建立不同节距下齿销啮合动力学模型,仿真得到不同节距下齿销啮合力曲线如图9所示。
销啮合力幅值随着销排节距增大而增大,齿销啮合力幅值分别为190、228和292 kN,最小节距时啮合力波动率为2.9%,最大节距时啮合力波动率为55.2%。说明适当减小节距可以降低齿销啮合力幅值和啮合力波动率,但过小的节距易使行走轮和销齿之间发生干涉。
4 齿销啮合特性的影响因素行走机构动力学特性受多种因素影响,单一的理论分析并不能直接反映各因素对行走机构动力学特性的具体影响,采用正交实验法可以探究不同工况下行走机构力学特性。
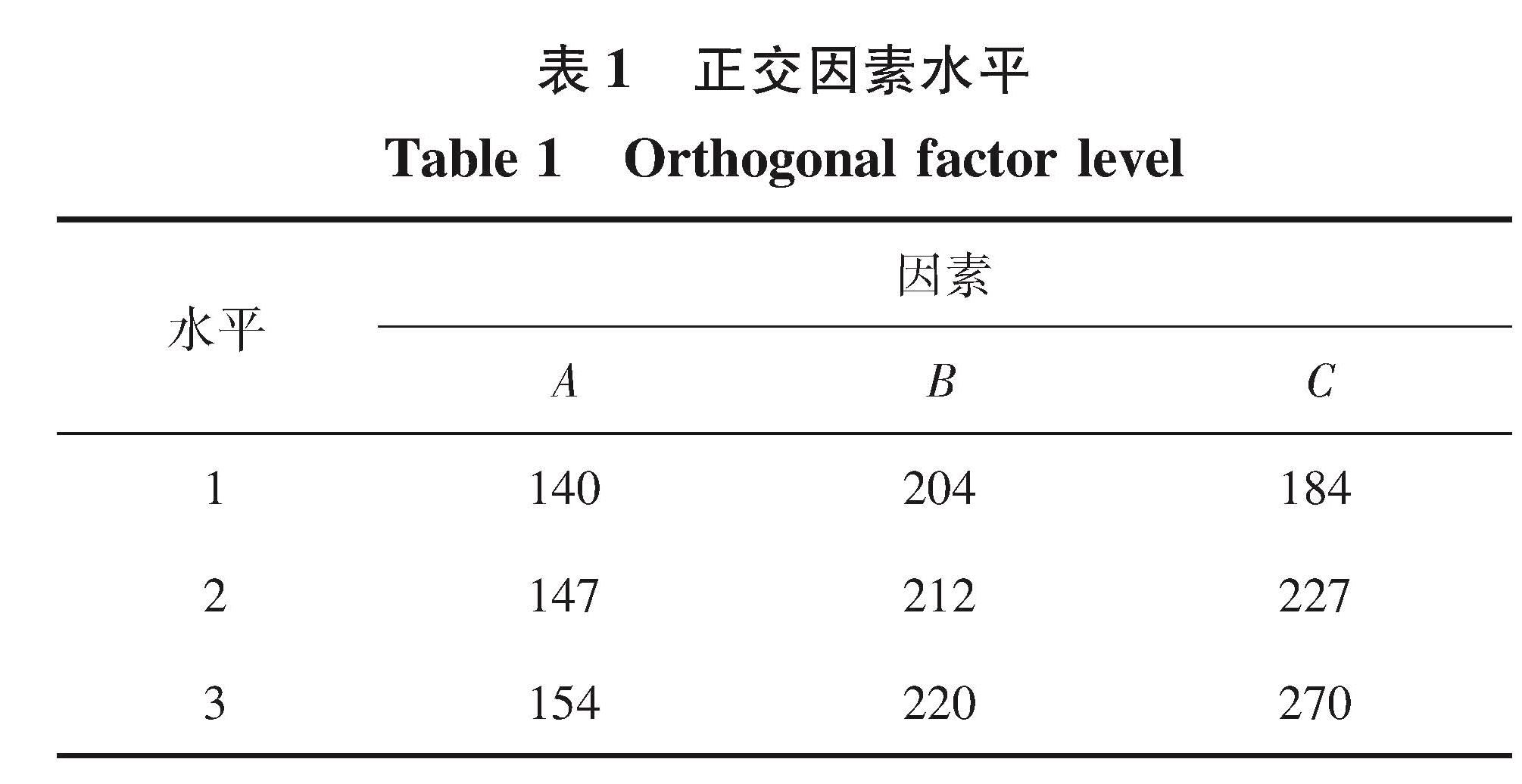
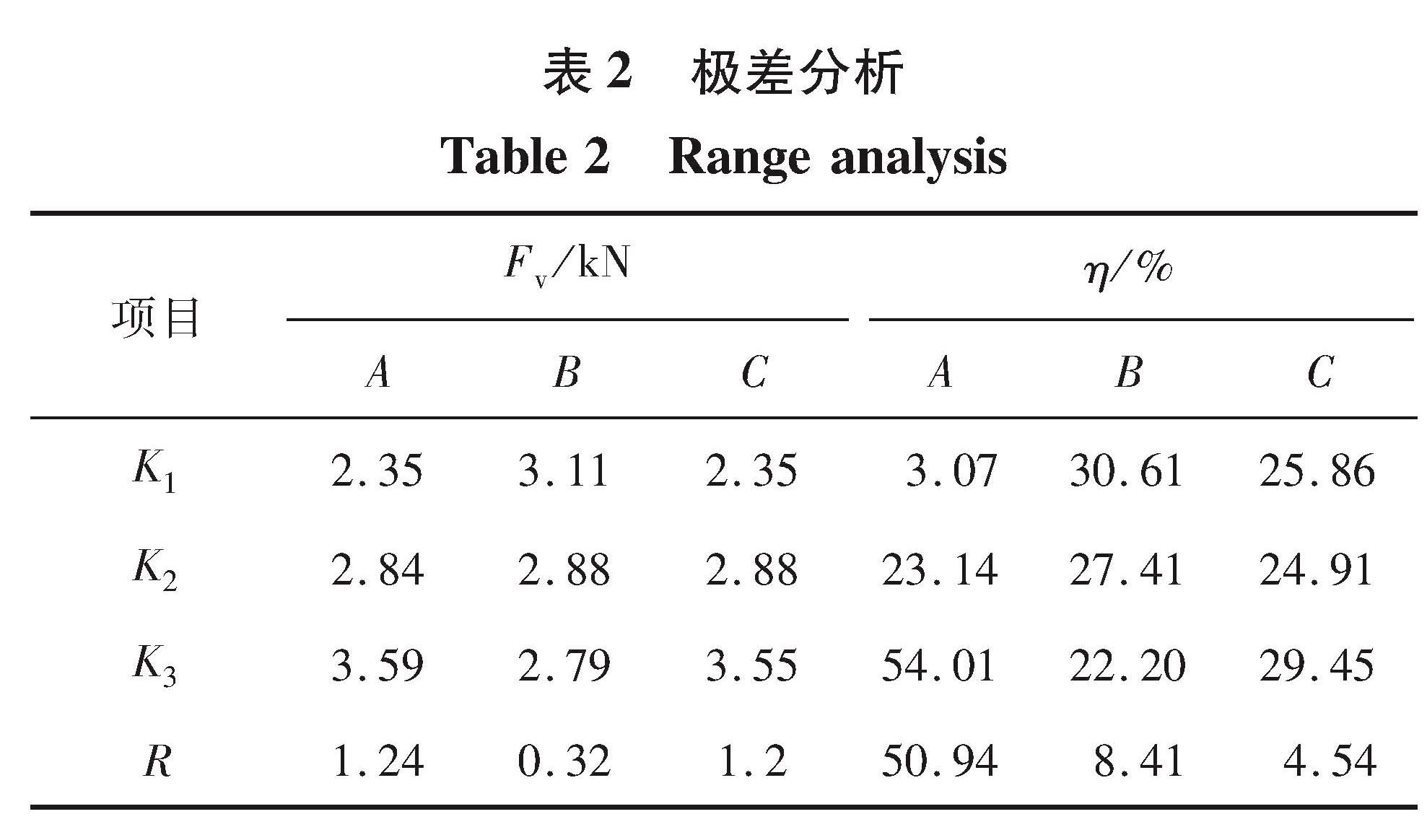
4.1 实验设计选取行走部啮合中心距、节距、煤层倾角为设计因素,按照 L9(33)正交表进行模拟实验,因素水平见表1。以行走部啮合力幅值Fv和啮合力波动率η为评价指标,对实验结果进行极差分析结果如表2所示。
4.2 实验结果分析
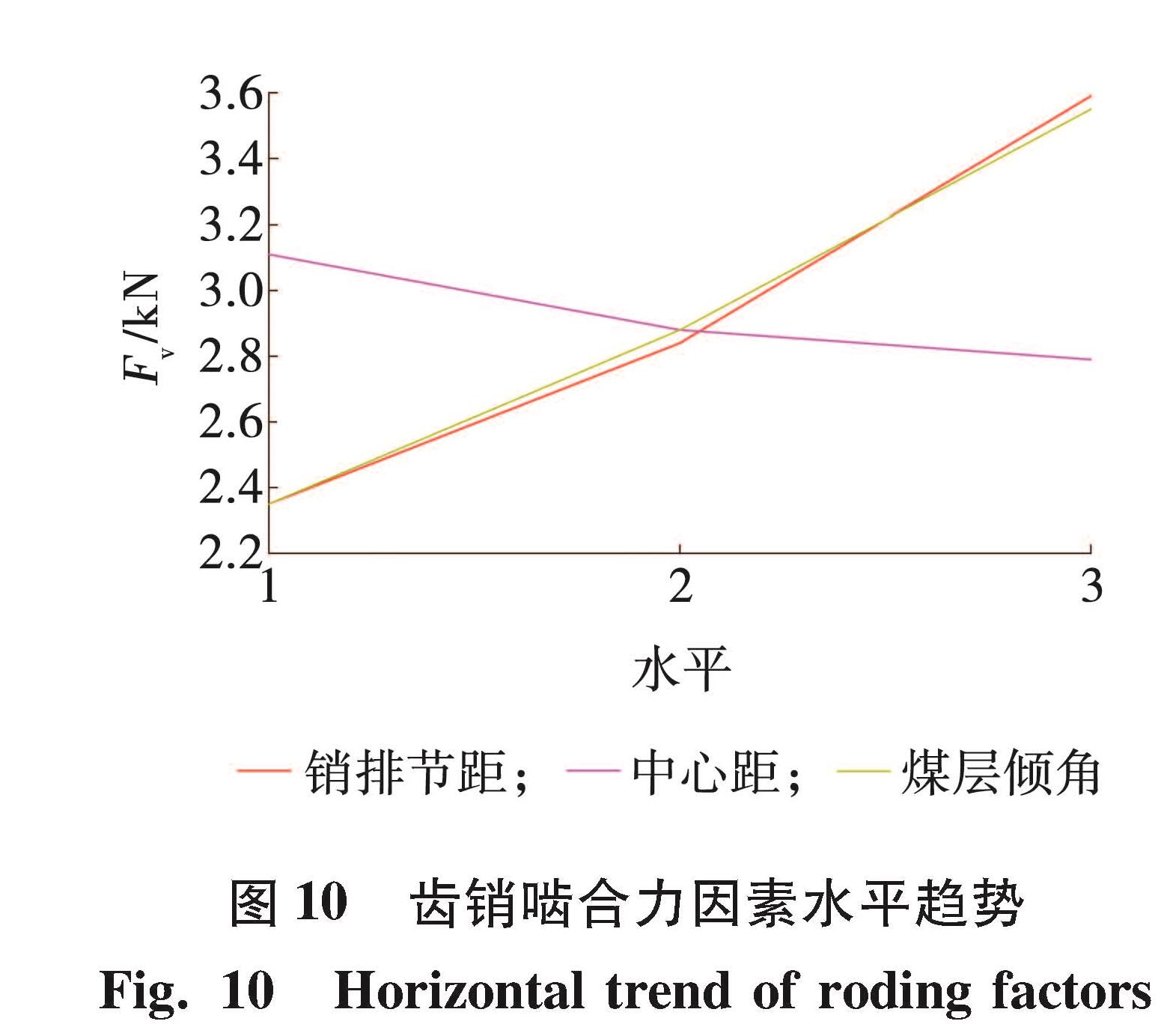
以各因素水平为横坐标,齿销啮合力幅值为纵坐标,经过数据处理得到各因素水平趋势如图 10所示。
通过极差分析法分析齿销啮合力幅值的主要影响因素,极差分析结果为 R(A)>R(C)>R(B),由极差分析结果可知,销排节距对齿销啮合力幅值影响最显著,中心距变化对齿销啮合力幅值影响较小。随着节距和煤层倾角增大,齿销啮合力幅值逐渐增大,原因是煤层倾角增大,机身重力沿牵引方向分量增大,随着节距增大行走轮与销齿初始啮合点靠近销齿圆弧上侧,压力角减小,导致齿销啮合力增大。
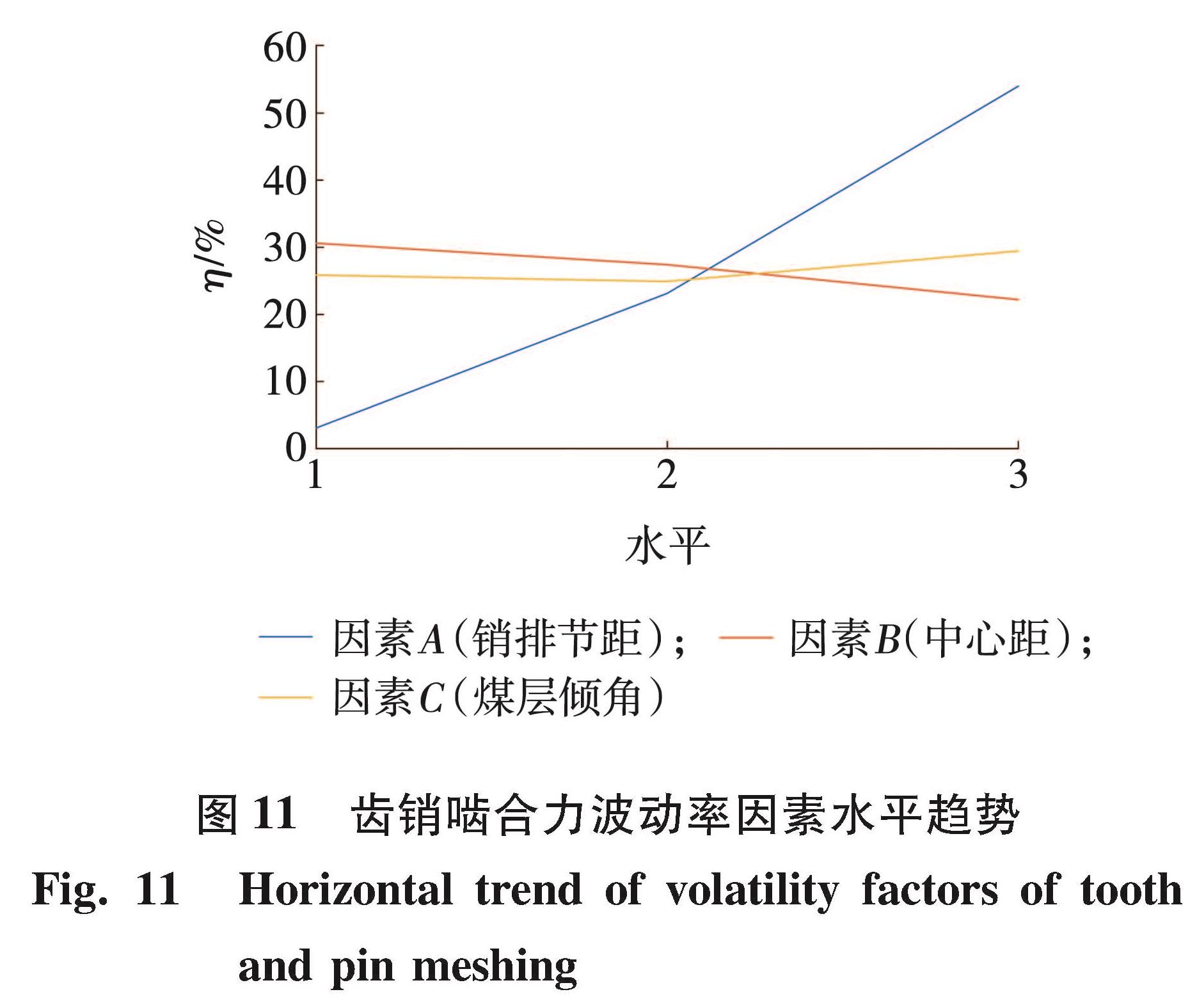
通过极差分析法对不同因素水平下齿销啮合力波动率进行分析,不同因素水平下齿销啮合力波动率如图 11所示。
极差分析结果为R(A)> R(B)>R(C),根据极差分析结果可知,销排节距变化对齿销啮合力波动率影响最显著,煤层倾角和啮合中心距变化对齿销啮合力波动率影响较小。随着销排节距增大齿销啮合力波动率显著增大,原因是随着节距增大行走轮与销齿初始啮合点靠近销齿圆弧上侧,压力角变大,且节距变化前后与直线段啮合时的压力角不变,导致齿销啮合力波动率增大。中心距变化和煤层倾角变化对齿销啮合力波动率影响较小,可知渐开线行走轮有较好的变中心距适应能力。
5 结 论(1)标准工况下,齿销啮合力波动周期约为0.88 s,波动周期与单齿啮合周期一致。行走轮与销齿圆弧段接触时啮合力达到最大值228 kN,与直线段啮合时啮合力较小,为186 kN,一个完整的啮合周期内啮合力波动率为22.5%。
(2)随着煤层倾角增大,牵引阻力和齿销啮合力不断增大,煤层倾角对牵引力波动率没有影响; 齿销啮合力及啮合力波动率均随中心距增大而减小,中心距最小比中心距最大时,啮合力幅值增加了约10.1%; 齿销啮合力幅值及啮合力波动率随着销排节距增大而增大,最大节距比最小节距时,齿销啮合力幅值增大约56%,最大节距时啮合力波动率为55.2%,最小节距时啮合力波动率为2.9%。
(3)对齿销啮合力幅值影响较大的因素是销排节距和煤层倾角,中心距对啮合力幅值影响较小。销排节距对齿销啮合力波动率影响较大,煤层倾角和齿销啮合中心距对啮合力波动率影响较小。
- [1] 葛世荣. 采煤机技术发展历程(三)电牵引采煤机[J]. 中国煤炭, 2020, 46(8): 1-15.
- [2] 郭松林, 张 伟. 采煤机运行位置伺服系统的滑模控制[J]. 黑龙江科技大学学报, 2017, 27(3): 251-255.
- [3] 张 丹, 齐立涛, 万 丰. MG2040型采煤机行走部件刚度对其动力学特性的影响[J]. 煤炭科学技术, 2017, 45(12): 150-154.
- [4] 刘春生, 田 操, 李孝宇. 大采高采煤机双列四驱动自适应调姿牵引方式研究[J]. 煤炭科学技术, 2016, 44(10): 125-130.
- [5] 吴卫东, 张志飞. 采煤机行走机构啮合参数对动力学特性的影响[J]. 黑龙江科技大学学报, 2014, 24(3): 256-261.
- [6] 张 鑫, 马德建, 曾庆良, 等. 不同载荷下采煤机行走机构动态特性研究[J]. 机械设计与制造, 2019(6): 244-246.
- [7] 毛 君, 田 松, 陈洪月. 斜切工况下刮板输送机销排载荷分析[J]. 机械传动, 2016, 40(4): 143-147.
- [8] 刘春生, 李德根, 任春平. 基于熵权的正则化神经网络煤岩截割载荷谱预测模型[J]. 煤炭学报, 2020, 45(1): 474-483.
- [9] 李德根, 程 硕, 刘延婷, 等. 碟盘刀具复合振动切削煤岩的损伤力学模型[J]. 黑龙江科技大学学报, 2021, 31(5): 673-678.
- [10] 黄冠华, 王兴宇, 梅桂明, 等. 内外激励下高速列车齿轮箱箱体动态响应分析[J]. 机械工程学报, 2015, 51(12): 95-100.
- [11] 刘春生, 于信伟, 任昌玉. 滚筒式采煤机工作机构[M]. 哈尔滨: 哈尔滨工程大学出版社, 2010.
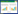 图 1 两对轮齿啮合刚度
Fig.1 Meshing stiffness of two gears
图 1 两对轮齿啮合刚度
Fig.1 Meshing stiffness of two gears