随着材料与技术的快速发展与应用,与时俱进的,人类对结构的优化设计有了更高的要求,而基于概率的可靠性优化设计是结构系统优化设计的重要分支。目前,计算结构可靠性指标的方法有中心点法[1]、验算点法[2]、蒙特卡罗法、响应面法[3]等。传统的结构优化设计方法有最佳矢量法和罚函数法等。这些传统的优化方法虽然精度很高,但是在面对复杂的工程结构时,就会出现求解困难,对全局最优解判定困难等缺点,缺乏实际工程价值。针对这些问题,有学者将群智能优化算法和结构系统可靠性优化设计领域相结合,很大程度上减少了计算过程。郑灿赫等[4]将粒子群算法和差分进化算法相融合,提出了一种混合算法,将其与结构可靠性优化其理论相结合。张水平等[5]通过对中心点进行随机替换对蜻蜓算法进行改进,提升了算法的寻优速度和精度。姜封国等[6]将教与学算法和禁忌搜索算法相结合,提出了混合教与学算法,并将其用于桁架结构的优化设计。以上学者对算法进行优化整合,在原有算法的基础上进行改进,大大提高了优化效率。Ranjini等[7]优化蜻蜓算法,提出了基于混合内存的蜻蜓算法,加快了算法的收敛速度。Ismail 等[8]利用混沌图调整了蜻蜓的运动参数,提出了混沌蜻蜓算法,使算法的收敛速度得到了提升。Zhang等[9]通过对蜻蜓行为进行量子化,提高了算法的寻优性能。上述改进方法在很大程度上改善了算法的优化效率。针对标准蜻蜓算法存在的缺陷,笔者提出基于t分布和Tent混沌映射的蜻蜓算法(TTDA),并且将之与结构可靠性优化设计结合,提出了在TTDA算法下的结构可靠性优化模型,通过算例验证其实用性。
1 蜻蜓算法蜻蜓算法(DA)通过模仿蜻蜓在自然界里的飞行规律和协作模式进行全局探索和局部开发,探索对应蜻蜓种群的长距离的移动,开发对应蜻蜓种群在小范围内的捕食行为。
蜻蜓群体的行为遵循着分离、结队、聚集、觅食和避敌。可以用以下5个数学公式来描述。
分离行为Si的公式为
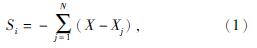
式中:X——蜻蜓个体目前所在的位置信息;
Xj——相邻第j个蜻蜓个体的位置信息;
N——蜻蜓周围相邻个体的数量。
结队行为Ai的公式为
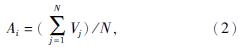
式中,Vj——相邻第j个个体的速度。
聚集行为Ci的公式为
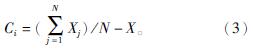
狩猎行为F</sup>i的公式为
Fi=X+-X,(4)
式中,X+——记录的食物所在位置,即目标最优解。
避敌行为Ei的公式为
Ei=X-+X,(5)
式中:X——蜻蜓个体当前的位置;
X-——天敌所在位置,即目标最差解。
上述5种行为可以得到蜻蜓个体位置移动的步长。
蜻蜓的邻域内有其他个体,则步长和位置向量的更新公式为
ΔXt+1=(sSi+aAi+cCi+fFi+eEi)+wΔXt,
Xt+1=Xt+ΔXt+1,(6)
式中:s——分离因子;
a——结对因子;
c——聚集因子;
f——狩猎因子;
e——避敌因子;
w——惯性权重;
t——迭代次数。
当该蜻蜓个体周围没有其他蜻蜓个体作为参照时,蜻蜓的位置将根据Levy飞行方程确定为
Xt+1=Xt+L(d)Xt,(7)
式中,d——向量维度。
L(d)具体函数信息为
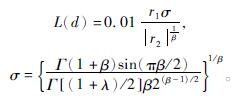
针对蜻蜓算法存在的不足之处,TTDA从两个方面进行改进:一是利用Tent混沌映射的特性改善蜻蜓种群的初始质量,以此来提高算法的收敛速度和全局探索能力。二是通过t分布对每个蜻蜓个体进行概率为50%的变异处理,将算法的迭代次数n作为t分布的自由度参数,在算法迭代的过程中利用高斯变异和柯西变异的特点提升算法的优化能力,以此加快收敛速度。
2.1 初始化种群为了提高初始种群的质量,利用混沌的遍历性、规律性等特点,将Tent映射生成的数据作为蜻蜓个体的初始位置信息,保留蜻蜓种群的多样性,提高算法效率。
原始的Tent映射数学公式为
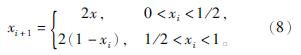
式(8)具备良好的随机性、遍历性、均匀性。映射实际上是将小数部分的二进制数向左移动,但这种映射有不足之处,因为计算机技术的限制,映射产生的混沌序列在迭代时有可能会陷入不稳定周期点。由文献[10]可知,混沌序列在点[0,0.25,0.5,0.75]处陷入不稳定周期点,为使映射产生的序列重新进入混沌状态,因此设计一种新的Tent混沌映射序列的产生方法,在原始的映射函数后加入一个随机变量为
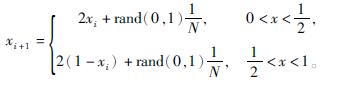 (9)
(9)
在这个随机变量的影响下,可以避免混沌序列落入循环。由式(9)得到混沌序列xt并通过式yt=lbi+(ubi-lbi)xt将结果逆映射到搜索空间中,得到更高质量的初始种群。
2.2 分布虽然混沌映射在一定程度上加快了算法的收敛速度,但是由于群智能算法本身的特性会导致算法在迭代过程中陷入局部最优并且难以跳出,使算法寻优效率过低。为进一步提升算法的寻优能力,有学者将高斯变异和柯西变异应用于群智能算法中来提升种群多样性,以跳出局部最小值,而高斯变异和柯西变异是t分布中的两个边界特例,因此文中将t分布融入蜻蜓算法中,避免算法陷入局部最优。
利用t分布去优化蜻蜓算法,对蜻蜓的个体位置进行t分布变异,变异的过程为
xti=xi+xit(n)λ/n,(10)
式中:xti——变异后种群里第i个蜻蜓个体新的位置;
xi——第i个蜻蜓个体的位置;
t(n)——满足将算法的迭代次数作为t分布的自由度;
n——迭代次数。
基于t分布的蜻蜓算法通过在原先蜻蜓的位置加上xit(n)服从t分布的干扰项,但是研究发现,随着迭代的进行,t(n)这个数值经常会出现大于1或小于-1的情况,其收敛不稳定,因此加上λ/n系数,使t的突变范围减小,有利于寻找更优的值,从而优化算法。
设置t分布中种群的变异几率为0.5,针对每只蜻蜓个体,都会生成一个[0,1]之间的随机数,当随机数小于变异概率0.5的视为满足变异条件的蜻蜓,并对其进行式(10)的t变异。
在蜻蜓算法刚刚开始迭代时,由于迭代次数少,t分布近似表现为柯西分布,此时对蜻蜓个体的扰动较强,算法具有较优的全局探索能力; 慢慢迭代次数开始增加,自由度n增加,t分布近似表现为高斯分布,算法会具有较强的局部开发性能。因此,通过t分布对蜻蜓算法进行优化,可以融合柯西分布和高斯分布的优点,提高算法的全局探索能力和局部开发性能。
2.3 改进的蜻蜓算法步骤将原始的蜻蜓算法与上述的优化方法相结合,提出了基于t分布和Tent混沌映射的混合变异算法。
首先初始化蜻蜓种群,初始化步长向量,蜻蜓个体搜寻上下限以及算法的权重系数等; 接着利用式(12)混沌初始化蜻蜓种群位置; 然后计算惯性权重w,以及s、a、c、f、e参数,并且根据式(1)至(5)计算S、A、C、F、E等因子,判断一个蜻蜓周围是否至少有一个邻近的蜻蜓,是则通过式(6)更新位置向量,否则通过式(7)莱维飞行方法更新位置向量; 最后根据更新的位置信息,以50%的概率针对每只蜻蜓进行t分布变异,通过式(10)更新其位置信息并计算其对应的适应度值,与前适应度值进行比较,保留更优的蜻蜓个体,达到最大迭代次数,则循环结束,输出最优解,否则进行下一次寻优过程。
3 结构可靠性优化分析方法3.1 可靠性优化模型对结构可靠性优化设计的研究已有几十年的历史,大致分为两阶段。第一阶段是以结构元件的可靠度指标作为约束条件建立优化模型; 第二阶段是以结构系统可靠度指标作为约束建立优化模型。文中实际是以结构元件的失效概率作为约束条件,建立可靠性优化模型,使所优化的结构质量最小。
桁架结构M的质量为
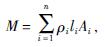
式中:ρi——构件的密度;
li——构件长度;
Ai——截面面积。
构件i的功能函数为
Zi=Ri-Si,
式中:R——构件容许应力的集合;
S——荷载的集合。
计算可靠性指标为
βi=(μZi)/(σZi),
式中:μ——功能函数的均值;
σ——功能函数的标准差。
元件失效概率和可靠性指标的数学公式为
Pfi=φ(-βi),
式中,φ——标准正态分布函数。
结构系统可靠性分析及设计优化问题是非常复杂的。在TTDA的可靠性优化设计中加入以下的收敛准则[11],以此来提高优化的稳定性和收敛速度。
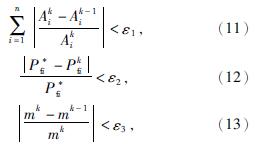
式中:k——迭代次数;
ε1、ε2、ε3——远小于1的数,10-4~10-3。
3.2 可靠性优化流程将改进后的混合变异蜻蜓算法应用到结构可靠性优化设计领域,建立以结构失效概率为约束条件下结构质量最小的数学模型。基于TTDA算法的可靠性优化步骤分为以下8步。
步骤1 设置参数,对每个蜻蜓个体的初始位置和初始步长向量进行初始化。
步骤2 利用式(9)生成的混沌序列映射到搜索空间得到初始化的蜻蜓种群。
步骤3 对需要优化的结构进行结构可靠性分析,判断结构是否满足数学模型的约束条件,若满足,则进行下一步。
步骤4 更新惯性权重w以及各权重系数s、a、c、f、e,通过式(1)至(5)计算蜻蜓群体五种行为因子S、A、C、F、E。
步骤5 如果一个蜻蜓个体周围至少有一个环绕着的蜻蜓,则通过式(6)变更位置向量,否则通过式(7)变更位置信息。
步骤6 对最新位置的蜻蜓个体进行t分布变异,保留变异后个体更优的蜻蜓。。
步骤7 若满足式(11)~(13)的收敛准则,则循环结束,保留最优的蜻蜓个体。否则返回步骤3。
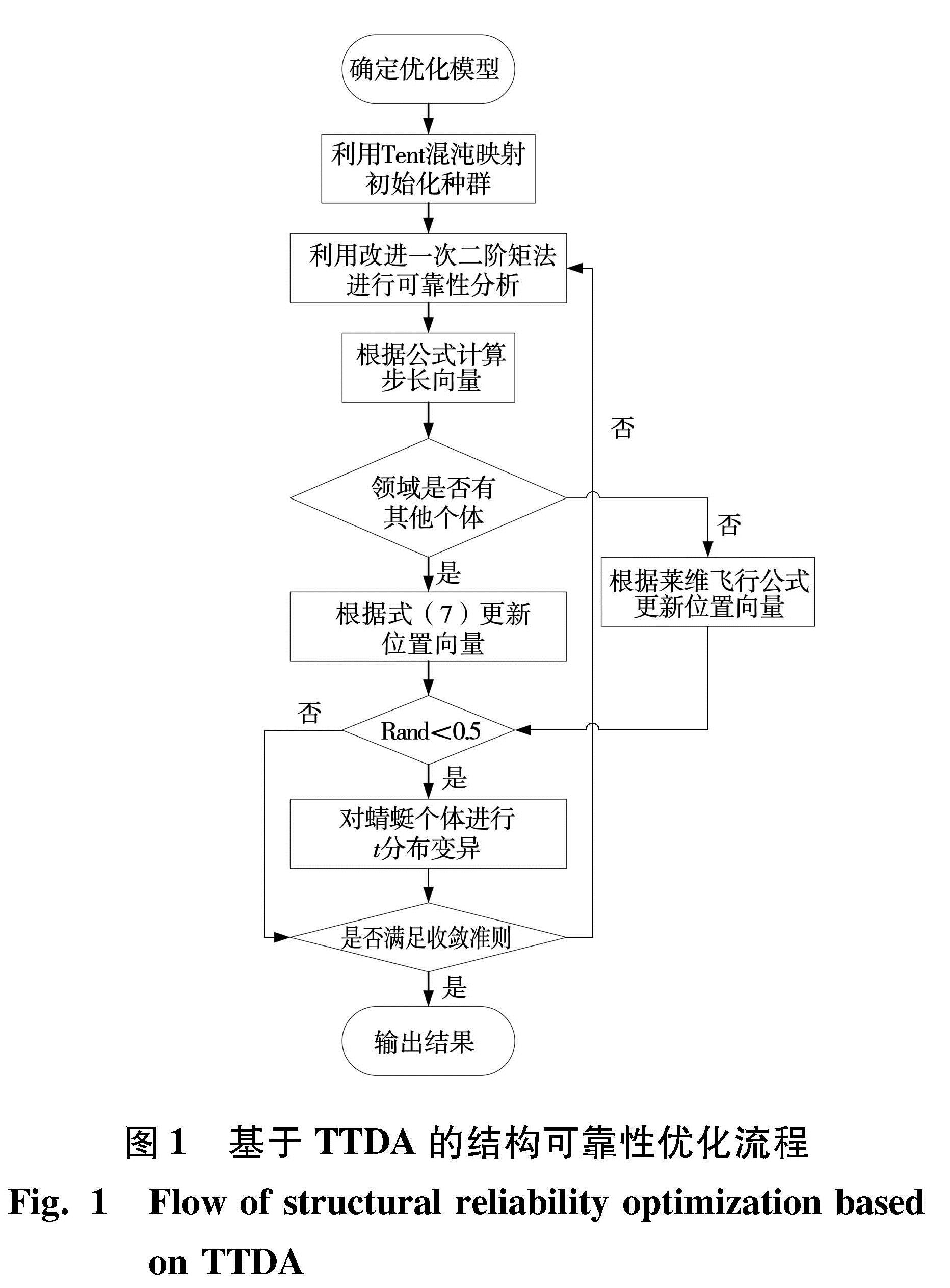
基于TTDA的结构可靠性优化流程如图1所示。
4 数值算例4.1 算例1
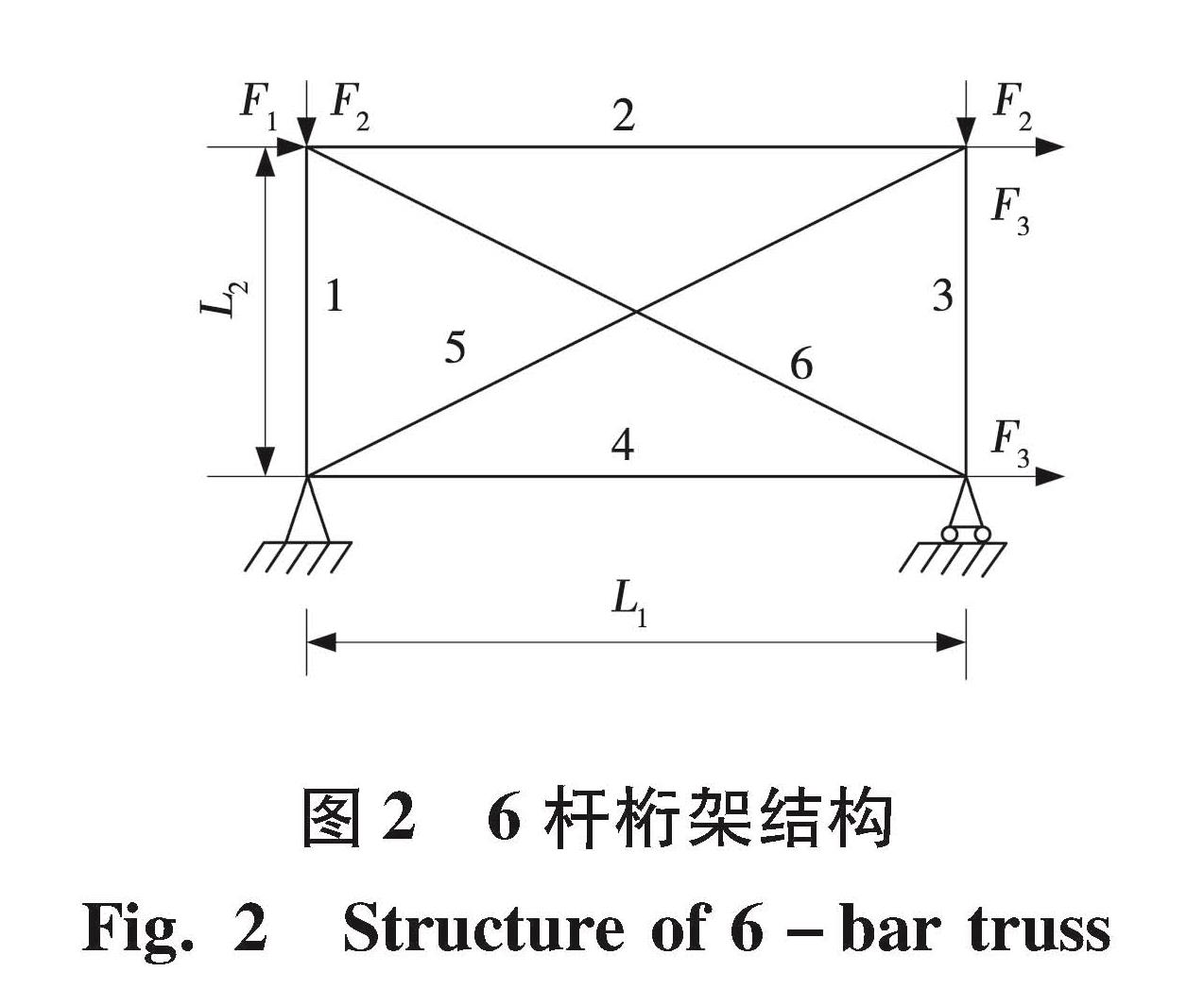
使用文中的优化方法对图2进行求解,该桁架结构的随机变量和相关参数:屈服应力的均值为27.6 kN/cm2,材料密度为2.7×10-3 kN/cm3,结构材料的弹性模量为7.06×103 kN/cm3,F1、F2、F3的均值分别为50、30、30 kN,结构容许可靠性指标βαs为3.239,结构横截面面积的上限为7 cm2,下限为3 cm2,ε1=ε3=2×10-4,ε2=10-4,在满足容许可靠性指标的前提下,利用TTDA算法求出结构的最小质量和各构件的横截面面积。
在两种具有代表性的荷载情况下,对该6杆桁架结构进化优化设计。工况Ⅰ:F1、F2、F3分别为46.225 3、28.224 7、16.009 5 kN。工况Ⅱ:F1、F2、F3分别为53.803 4、23.945 4、16.099 5 kN,文中的维度是6。
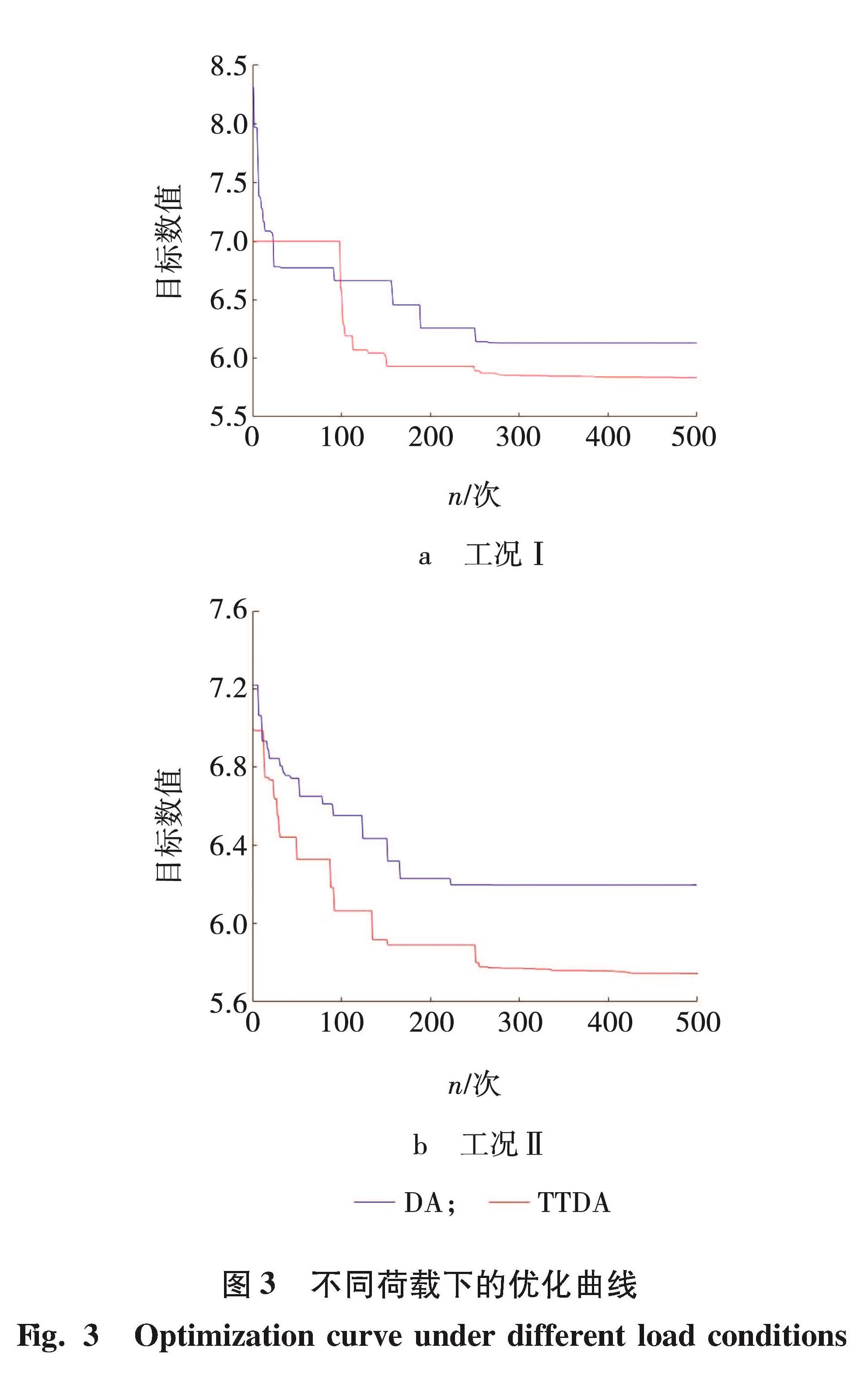
在相同的条件下,对本桁架结构结合DA算法和TTDA算法进行可靠性优化计算,工况Ⅰ、Ⅱ的结果如图3所示。
由图3a可知,在工况Ⅰ的荷载条件下,TTDA算法在迭代250次时会达到目标函数值5.945 6,随着迭代次数的进行,达到了最优值5.834 5,但DA算法在迭代250次的时达到目标数值6.130 9。由图3b可知,TTDA算法在迭代250次附近时达到函数值5.856 7,并且随着迭代次数的增加达到目标函数值5.745 1,而DA算法在迭代250次左右才达到目标函数值6.197 5。并且迭代次数在250次附近时,DA算法已经开始收敛,而TTDA算法随着迭代次数的增加精度还有略微增加。由此可知,TTDA算法的优化效果要好于DA算法,并且在寻优中期时迭代速度要高于DA算法,在迭代后期收敛精度要好于DA算法。
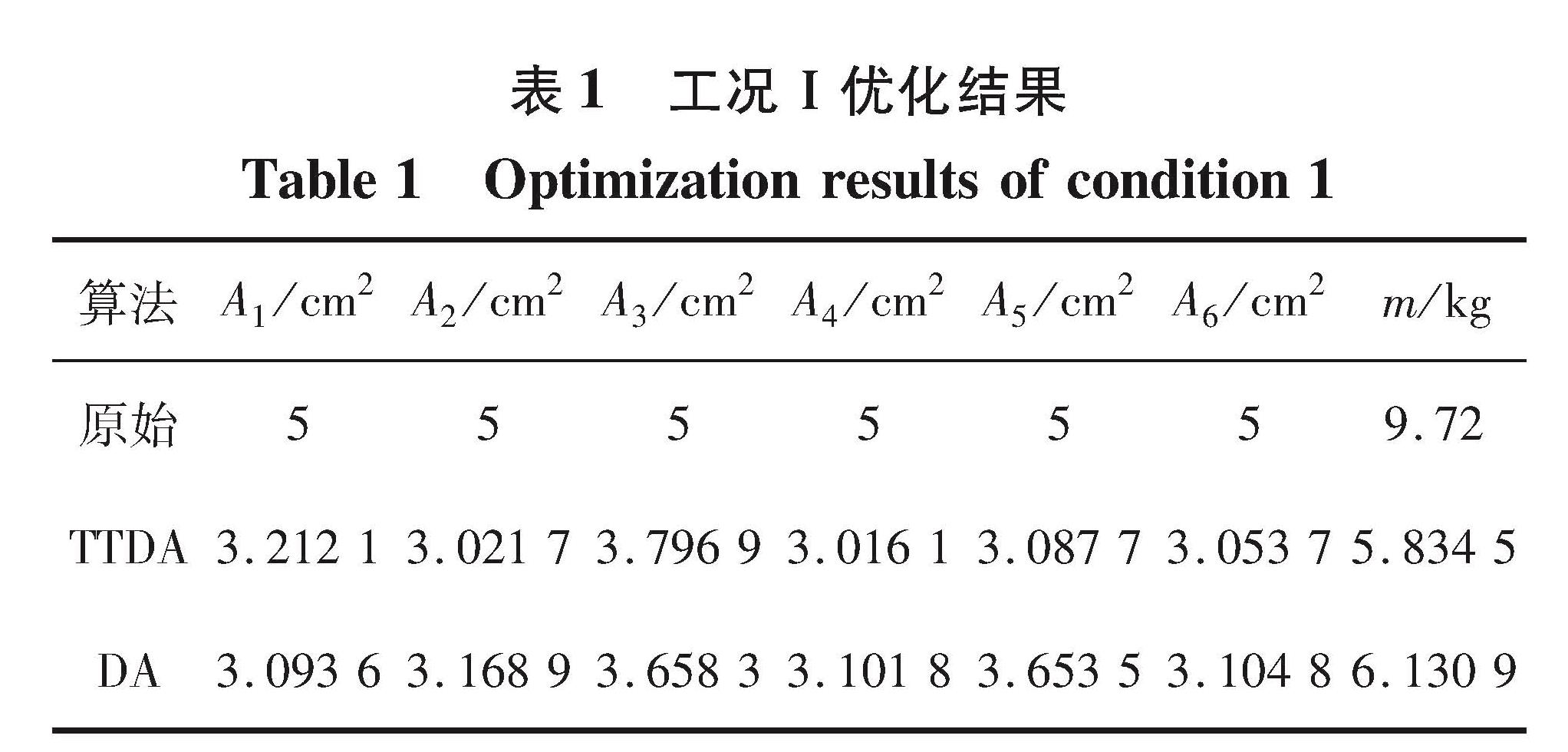
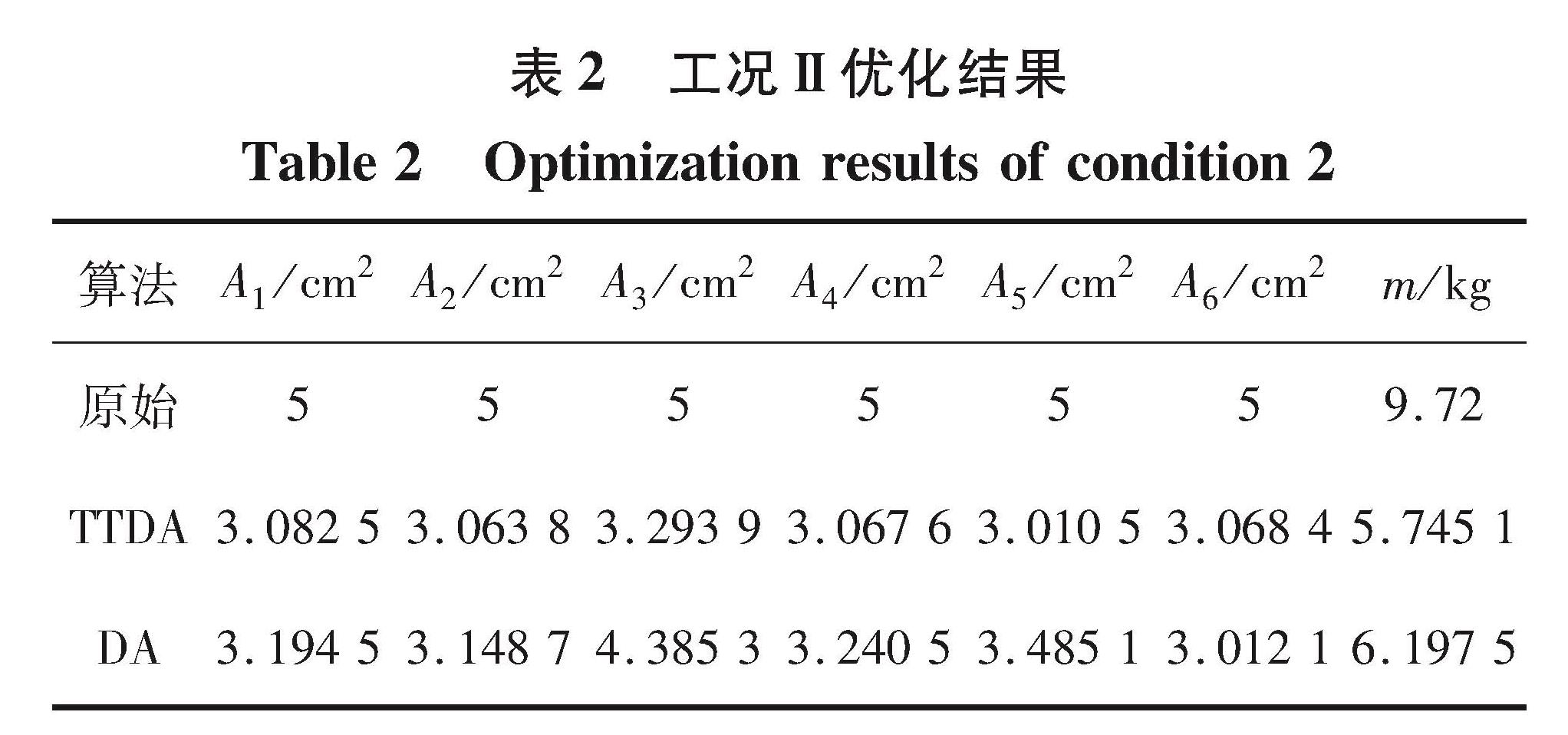
表1和2分为别两种荷载情况下TTDA算法和DA算法的优化结果,在荷载工况Ⅰ的条件下,基于TTDA算法的结构质量优化结果为5.834 5 kg,基于DA算法的质量优化结果为6.130 9 kg; 在载荷工况Ⅱ的条件下,基于TTDA算法的结构质量优化结果为5.745 1 kg,基于DA算法的结构质量优化效果为6.197 5 kg,由此可见,相比较于DA算法,TTDA算法有着更好的优化性能。
从表1和2可以看出,基于TTDA算法的结构可靠性优化结果要比DA算法更好,在可靠性约束条件下使各截面面积最小可以节省材料,结果表明,TTDA算法收敛更快,精度更高。
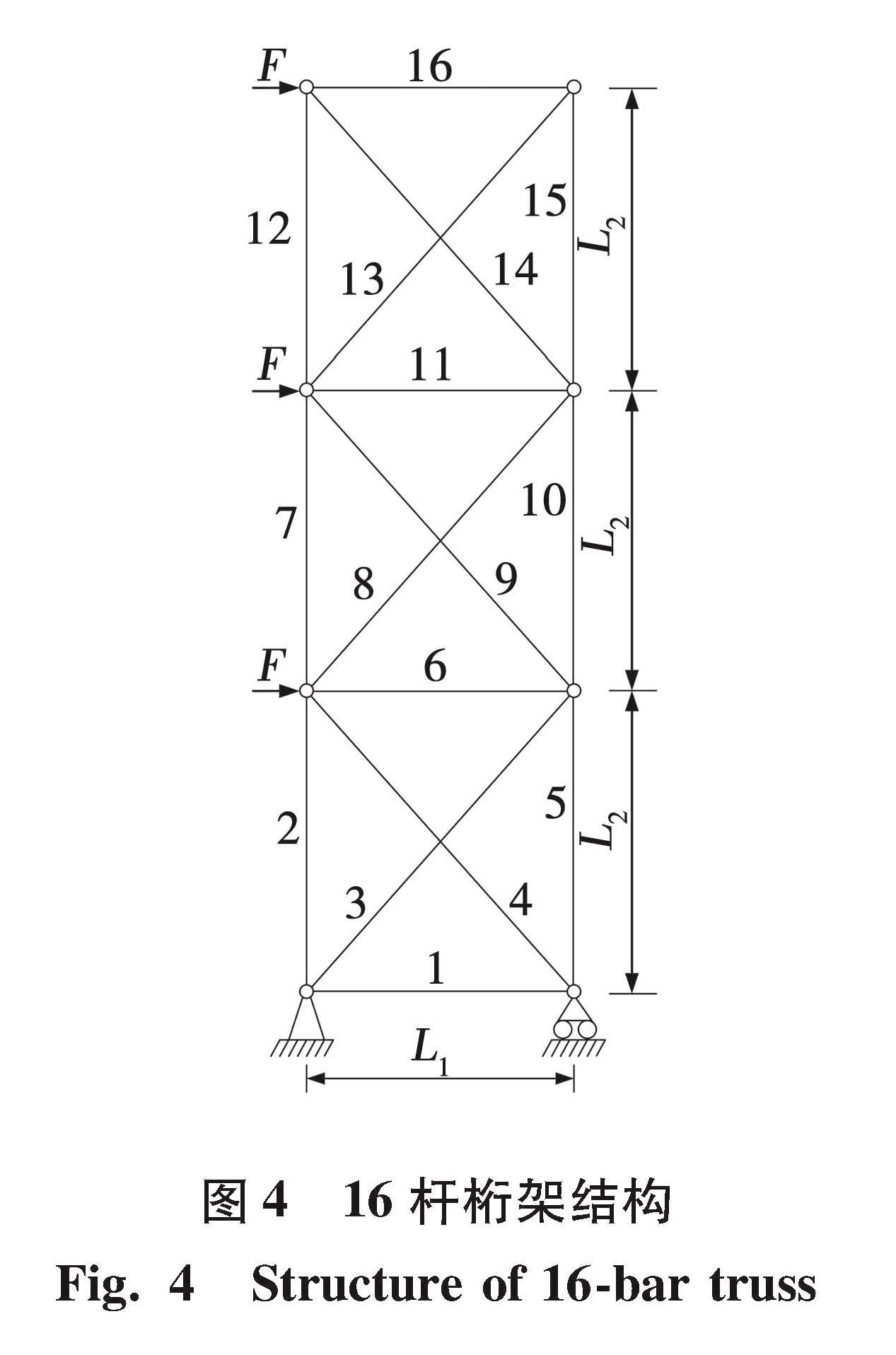
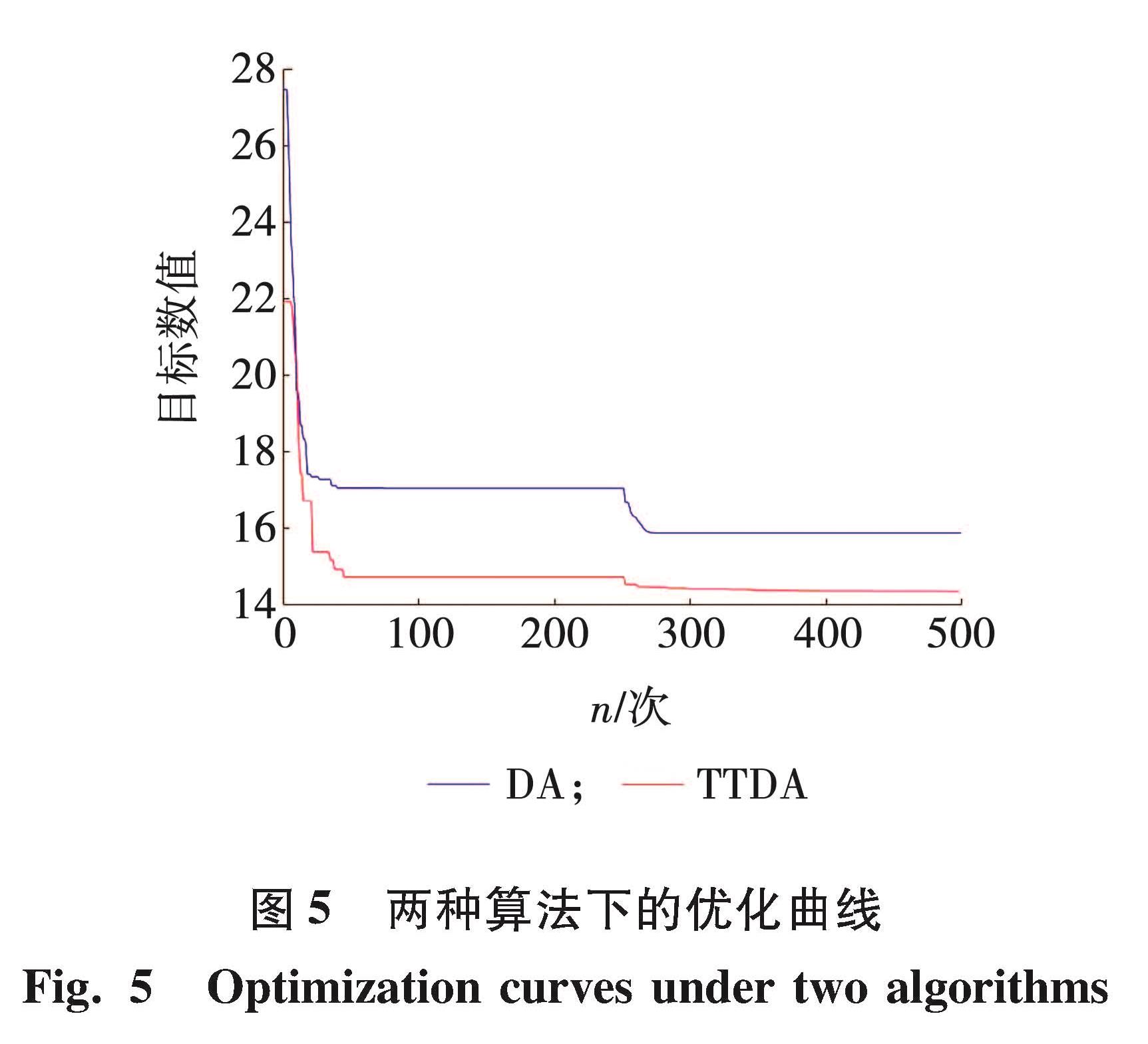
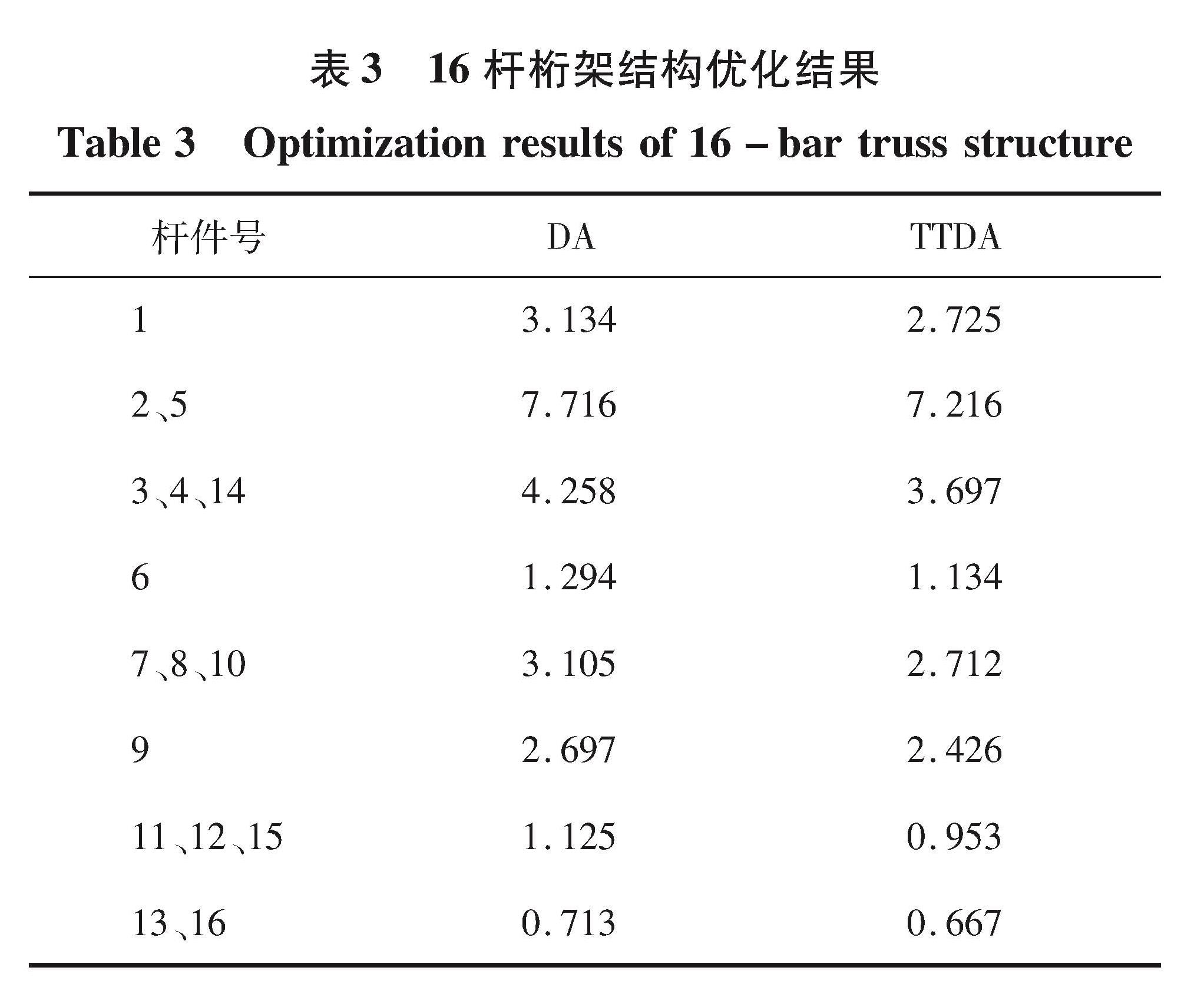
4.2 算例2一个16杆超静定桁架如图4所示,结构参数:屈服应力均值为276 MPa,变异系数CR为0.05,弹性模量E=2.06×105 MPa,材料的密度ρ为2.7×103 kg/m3,荷载均值F为44.45 kN,变异系数CF为0.1,不确定设计变量连接关系为A1,A2=A5,A3=A4=A14,A6,A7=A8=A10,A9,A11=A12=A15,A13=A16,杆件之间只有独立或相关两种情况。设个体数为100,最大迭代次数为500。16杆桁架结构的优化结果如表3所示,两种算法优化曲线如图5所示。
由图5可知,混合变异蜻蜓算法收敛更快,结果更优。
蜻蜓算法和混合变异蜻蜓算法的优化结果分别为15.88和14.36 kg,TTDA算法的优化结果明显优于DA算法。
5 结 论(1)在原始的DA算法中,通过t分布变异和Tent混沌映射函数两种方法对DA算法进行改进,提高了DA算法的收敛速度和精度,提出了一种基于t分布和Tent混沌映射的TTDA算法。
(2)将文中所改进的TTDA算法用于可靠性优化设计中,算例1结果表明,TTDA算法比原始的DA算法能优化出更好的结果,在两种不同的工况条件下,TTDA算法比DA算法分别减少了4.83%和7.3%。算例2结果表明,TTDA算法相对于原始DA算法减少了9.5%,说明该算法可以为结构可靠性优化设计提供一种新的优化方法。
- [1] Cornell C A. A probability based structural code[J]. A CI Journal of the American Concrete Institute, 1969, 6(12): 974-985.
- [2] Hasofer A M, Lind N C. Exact and invariant secondm -oment code format[J]. Journal of the Engineering Mec -hanics, ASCE, 1974, 100(1): 111-121.
- [3] 高亚强, 王兴国. 基于可靠性的结构优化设[J]. 河北理工大学学报(自然科学版), 2008(1): 120-123.
- [4] 郑灿赫, 孟广伟, 李 峰, 等. 基于PSO-DE混合算法的结构可靠性优化设计[J]. 华南理工大学学报, 2014, 42(9): 41-45.
- [5] 张水平, 高 栋. 基于随机替换和混合变异的蜻蜓算法[J]. 科学技术与工程, 2020, 20(22): 9108-9115.
- [6] 姜封国, 郭 威, 王路瞳, 等. 基于混合教与学算法的结构可靠性优化设计[J]. 黑龙江科技大学学报, 2021, 31(4): 525-530.
- [7] Ranjini S K S, Murugan S. Memory based Hybrid Dragonfly Algorithm for numerical optimization problems[J]. Expert Systems with Application, 2017, 83(8): 63-78.
- [8] Ismail S G, Alaa T, Ella H A. Chaotic dragonfly algorithm:an improved meta heuristic algorithm for feature selection[J]. Applied Intelligence, 2018, 49(1): 188-205.
- [9] Zhang Z, Hong W C. Electric load forecasting by complete ensemble empirical mode decomposition adaptive noise and support vector regression with quantumbased dragonfly algorithm[J]. Nonlinear Dynamics, 2019, 98(1): 1107-1136.
- [10] 张 浩, 张铁男, 沈继红, 等. Tent混沌粒子群算法及其在结构优化决策中的应用[J]. 控制与决策, 2008, 23(8): 857-862.
- [11] 安伟光, 蔡荫林, 陈卫东. 随机结构系统可靠性分析与优化[M]. 哈尔滨: 哈尔滨工程大学出版社, 2007.
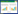 图 1 基于TTDA的结构可靠性优化流程
Fig.1 Flow of structural reliability optimization based on TTDA
图 1 基于TTDA的结构可靠性优化流程
Fig.1 Flow of structural reliability optimization based on TTDA