随着开采深度的增加,工作面及采空区应力场愈加复杂,工作面来压现象及采空区围岩破坏程度也愈加严重。对顶板的破断垮落规律的研究分析是保障和促进安全生产的重要方法。
目前对采场覆岩的研究中,许延春等[1-2]根据多个综采工作面的“两带”高度,通过回归分析获得了不同覆岩类型下“两带”高度的经验公式。刘红威等[3]通过结合理论分析、数值模拟和现场实测的方法,对切顶成巷工况下的覆岩破坏规律及裂隙发育特征进行了研究。武猛猛等[4]在PFC2D中通过构建采场模型的方式研究了采场初次来压期间上覆岩层的破坏规律及裂隙发育特征。以上学者分别从理论角度和实际角度对顶板的破坏及裂隙发育规律进行了研究和探讨,但顶板中关键层破断距的计算对工程实践中预测工作面顶板来压等现象更具有参考意义。
岩层的破断是顶板垮落过程中的必然现象,但将理论计算与现场实测数据的对比和验证发现,将岩层简化为简支梁或固定梁,只适用于计算近煤层覆岩的垮落距[5-6]。故部分学者逐渐将破断面和破断角的概念加入对顶板垮落规律的研究中,如许斌等[7]结合弹性力学和岩体力学研究了关键层破断时的力学状态,推导了关键层破断角的计算公式。贺雁鹏等[8]采用钻孔窥视技术,通过几何分析反演获得了工作面覆岩的破断角,并结合物理模拟试验验证了破断角的理论计算公式。笔者在以上学者对破断角规律和理论研究的基础上,结合破断角的理论计算公式,进一步推导覆岩中关键层初次垮落距的计算公式,并利用数值模拟试验对其进行验证。
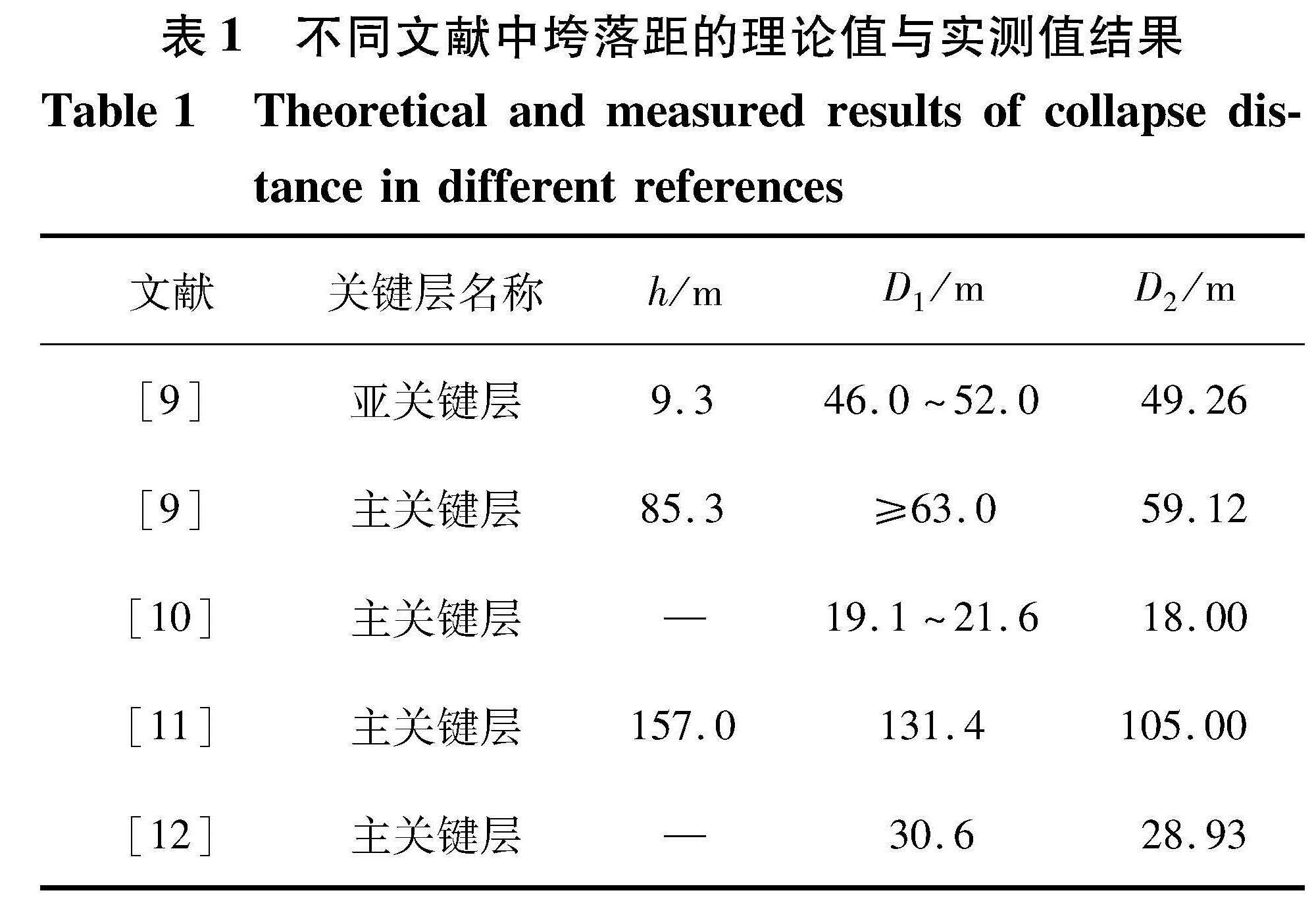
1 结合破断角的关键层垮落距1.1 案例分析随着煤矿资源的开采,煤矿工况的复杂程度逐渐增加,如采场上方关键层层数多、主关键层距采场远的岩层分布情况,顶板垮落带随采空区厚度的增加而扩大的现象。同时,部分工况中出现现场测定的实际垮落距D1明显高于根据简支梁或固定梁理论计算的极限跨距D2(表1),且理论值和实际测量值的差值随着关键层与煤层的距离h增加而出现明显增幅,这与破断面对覆岩的影响相对应。但受岩层力学性质不同的影响,岩层的破断形状及破断角的大小规律有所差异,故需结合破断角的理论和计算方法,推导关键层的初次破断距。
表1 不同文献中垮落距的理论值与实测值结果
Table 1 Theoretical and measured results of collapse distance in different references
1.2 破断角理论及计算方法
破断面、水平面及最大主应力的位置关系如图1所示,由图1中可知,破断角β可通过分别计算最大主应力σ1与水平面及破断面的夹角θ1、θ2求得,即β=θ1+θ2。而根据摩尔库伦准则可知,岩石剪切破坏面与最大主应力的夹角θ2=φ/2+45°(φ为岩石内摩擦角)[13],故β只需通过求解θ1即可获取。
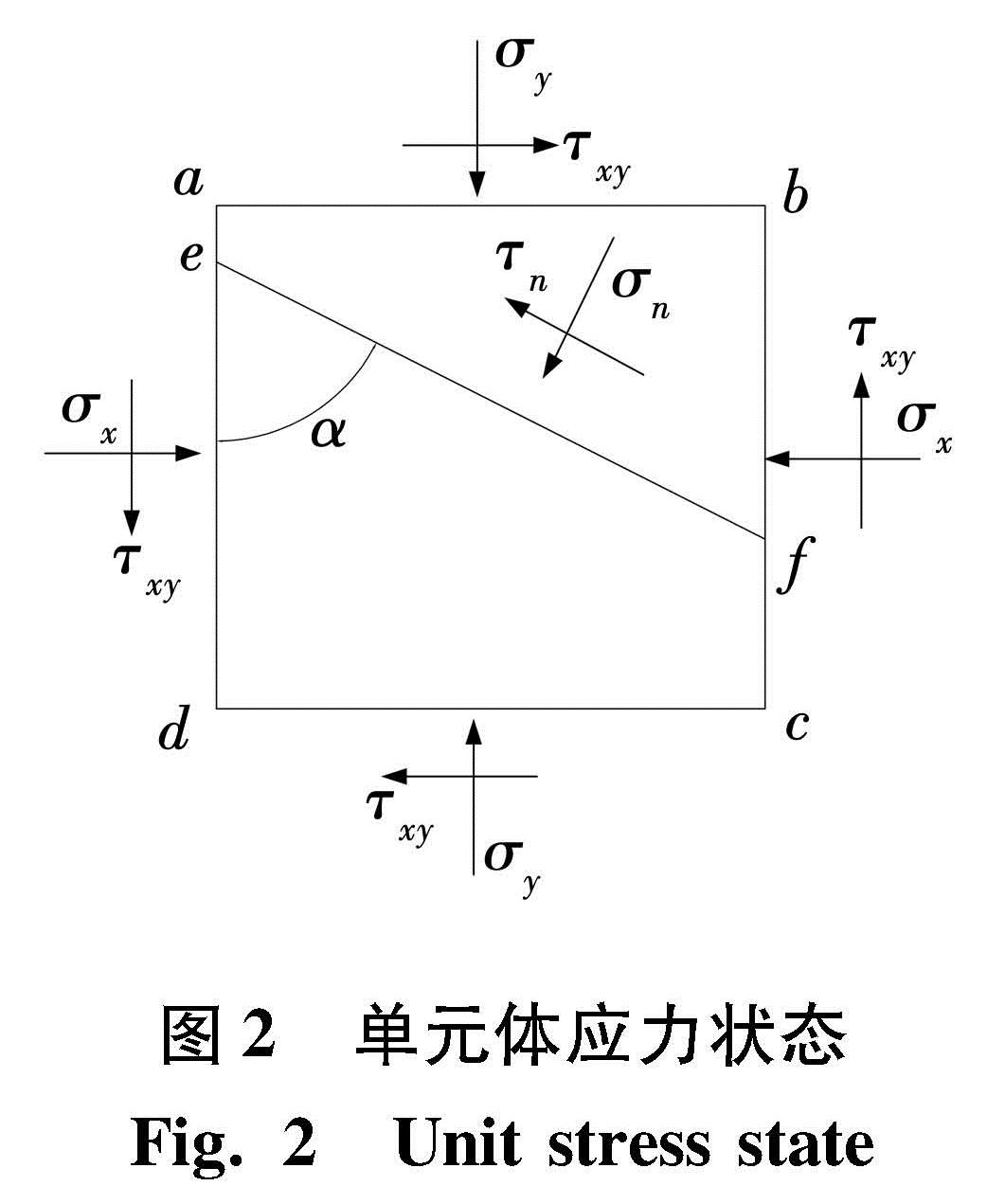
岩层破断前体内任一单元的受力图如图2所示,对弹性力学与岩体力学中斜截面ef的应力平衡方程进行求导推算,可求得最大主应力σ1与水平应力σx夹角α0的函数方程为
tan 2α0=-(2τxy)/(σx-σy)。(1)
文献[7]推导出的关键层岩梁应力分解量为
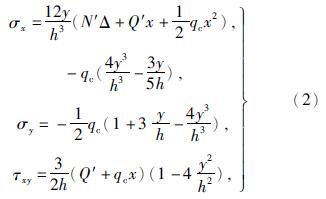
式中:Δ——岩层受应力产生的弯曲扰度;
N'——岩层自由端所受水平应力;
Q'——岩层自由端所受垂直应力;
qc——岩层块体上表面均匀载荷;
h——岩层块体厚度。
将式(2)代入式(1),进行角度转换可求得θ1为
θ1=1/2arctan(3L)/h,(3)
式中,L——悬挂岩层块体长度。
将式(3)及θ2代入式(1)中可得破断面与水平面夹角β为
β=(π)/4-φ/2+1/2arctan(3L)/h。(4)
1.3 垮落距计算对现场工况分析时,通过将岩层视为材料力学中的固支梁,根据梁的极限抗拉强度可求得岩层初次垮落和随上覆关键层破断时的极限破断距估值为
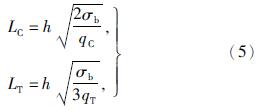
式中:σb——岩层极限抗拉强度;
qC——关键层初次垮落所受的载荷;
qT——随上覆关键层同步垮落时岩层所受的载荷。
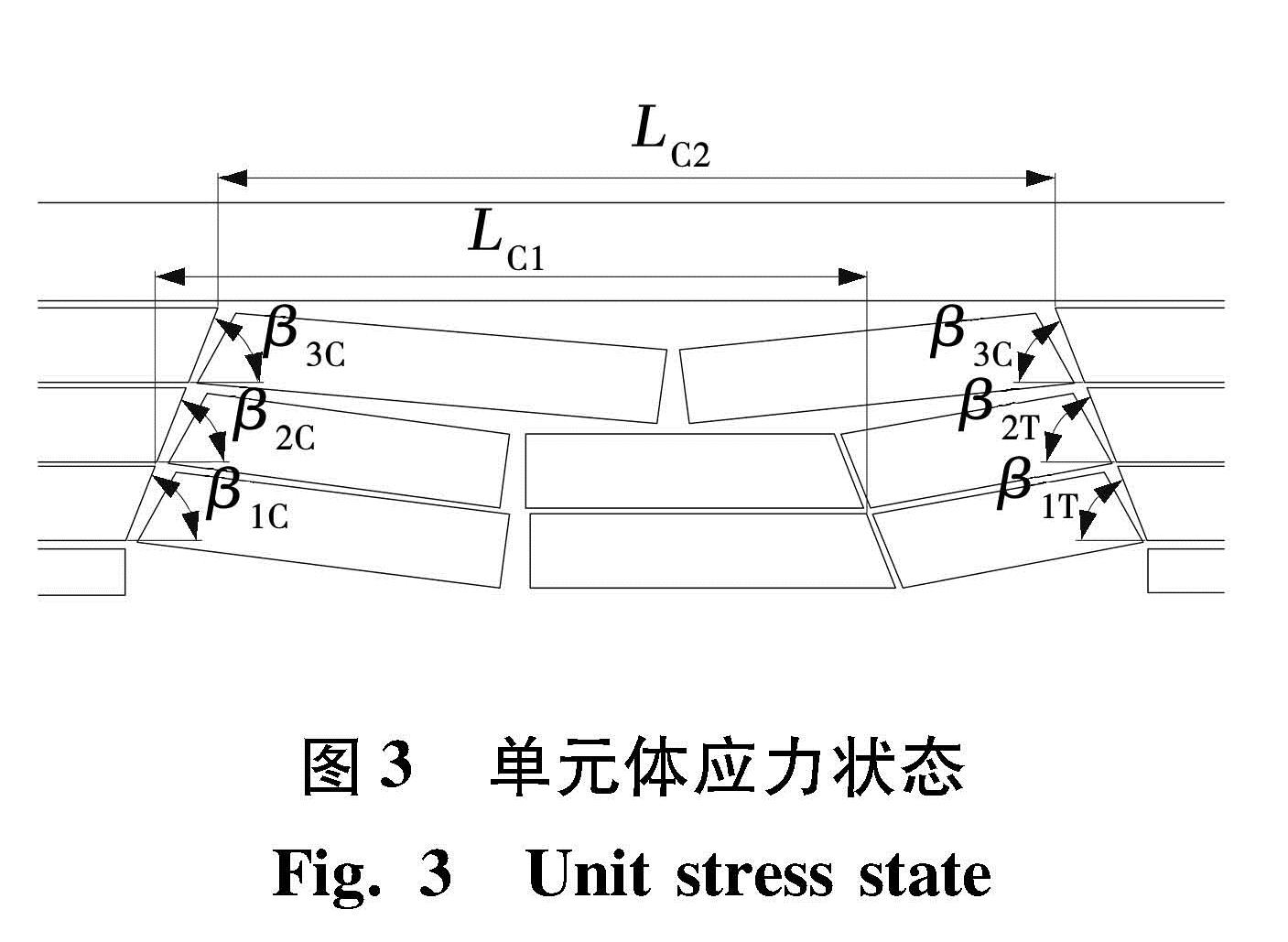
但当煤层推进距离达到极限垮落距时,岩层顶部两端在拉应力作用下会率先发生破坏,裂缝沿破断面向两侧分别发展至开切眼和工作面上方,如图3所示。
当顶板内关键层离开挖煤层较远或关键层的极限垮落距较小时,关键层的初次垮落距需在考虑极限垮落距的基础上,累加关键层及以下岩层破断面的横向跨越距离。
根据图3中的几何关系,可求得考虑破断角时各关键层的初次垮落距分别为
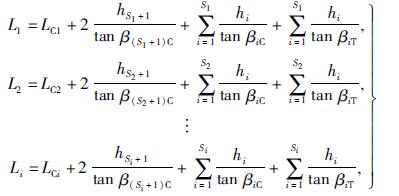 (6)
(6)
式中:LCi——埋深从深至浅各关键层的极限跨距,i=1,2,…,n;
Si——各关键层至煤层间岩层层数,i=1,2,…,n;
βiC——第i层顶板初次垮落时的破断角;
βiT——第i层顶板随关键层同步发生破断时的破断角;
hi——第i层顶板厚度。
2 采场数值模拟2.1 数值模型构建颗粒流软件PFC2D作为离散元程序,通过二维圆盘颗粒及黏结键生成的材料在外力作用下可破坏,适合考虑破坏及变形的研究。模型宽高为55 m×100 m(图4)共模拟了煤岩15层,模型水平方向边界及垂直方向底板分别通过柔性颗粒束缚水平和垂直方向的位移,并通过柔性加载对模型顶部施加600 m岩层重量的载荷来还原模型所在岩层的原岩应力。同时为减少模型开挖时的计算量,圆盘颗粒在考虑不同岩层厚度的情况下预设不同粒径范围。模拟开采煤层为高度1.45 m的7#煤,左侧预留15 m煤柱,工作面从左向右推进,开挖推进速度为1.6 m/次。
2.2 参数标定
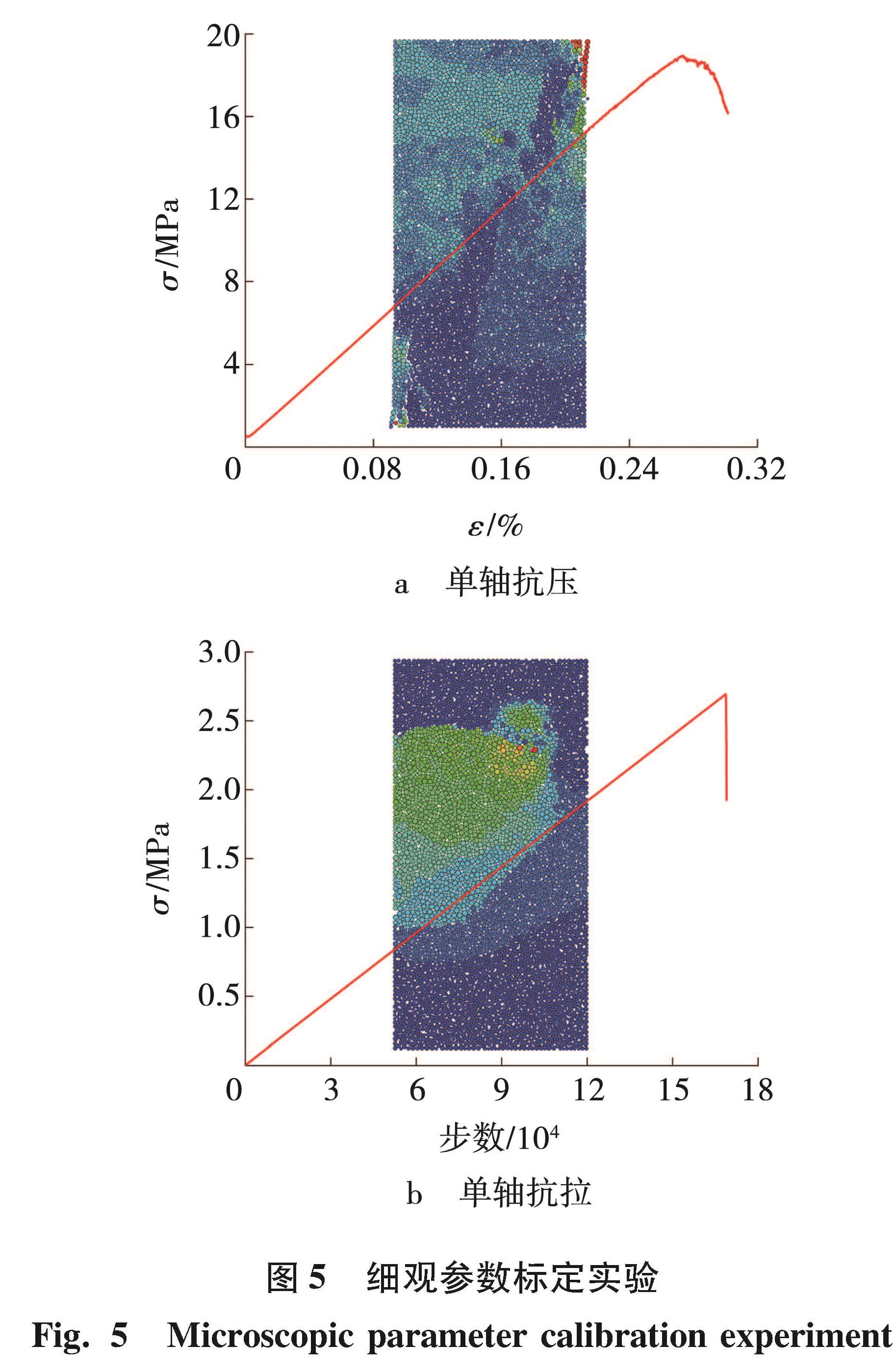
颗粒流程序PFC模拟煤岩体时,需通过不同的接触模型生成模型,文中选用无黏结状态下仍为面-面接触的平节理模型(Flat-joint contact model)构建数值模型。同时考虑到颗粒细观参数与模型宏观参数的差异性,文中参考岩石的单轴物理实验,通过PFC2D模拟单轴抗压-抗拉试验(图5)的方式对模型细观参数进行标定。
在平节理模型中,材料的细观参数主要包括法向刚度kn、切向刚度ks、刚度比k*=kn/ks、平节理抗拉强度σc、平节理黏结强度C、容重ρ、摩擦系数μ及摩擦角φ。其中模型的每层岩石刚度比k*设置为2,摩擦因数μ及摩擦角φ可直接通过宏观参数标定; 而细观参数法向刚度kn及平节理抗拉强度σc分别对材料的宏观参数弹性模量E及抗拉强度σt有决定性影响,因此通过控制变量及线性拟合的方式,分别获得由弹性模量E和抗拉强度σt估算法向刚度kn和平节理抗拉强度σc的简易方程为
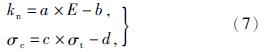
式中:a=19.851; b=0.033 2; c=1.81; d=0.216。
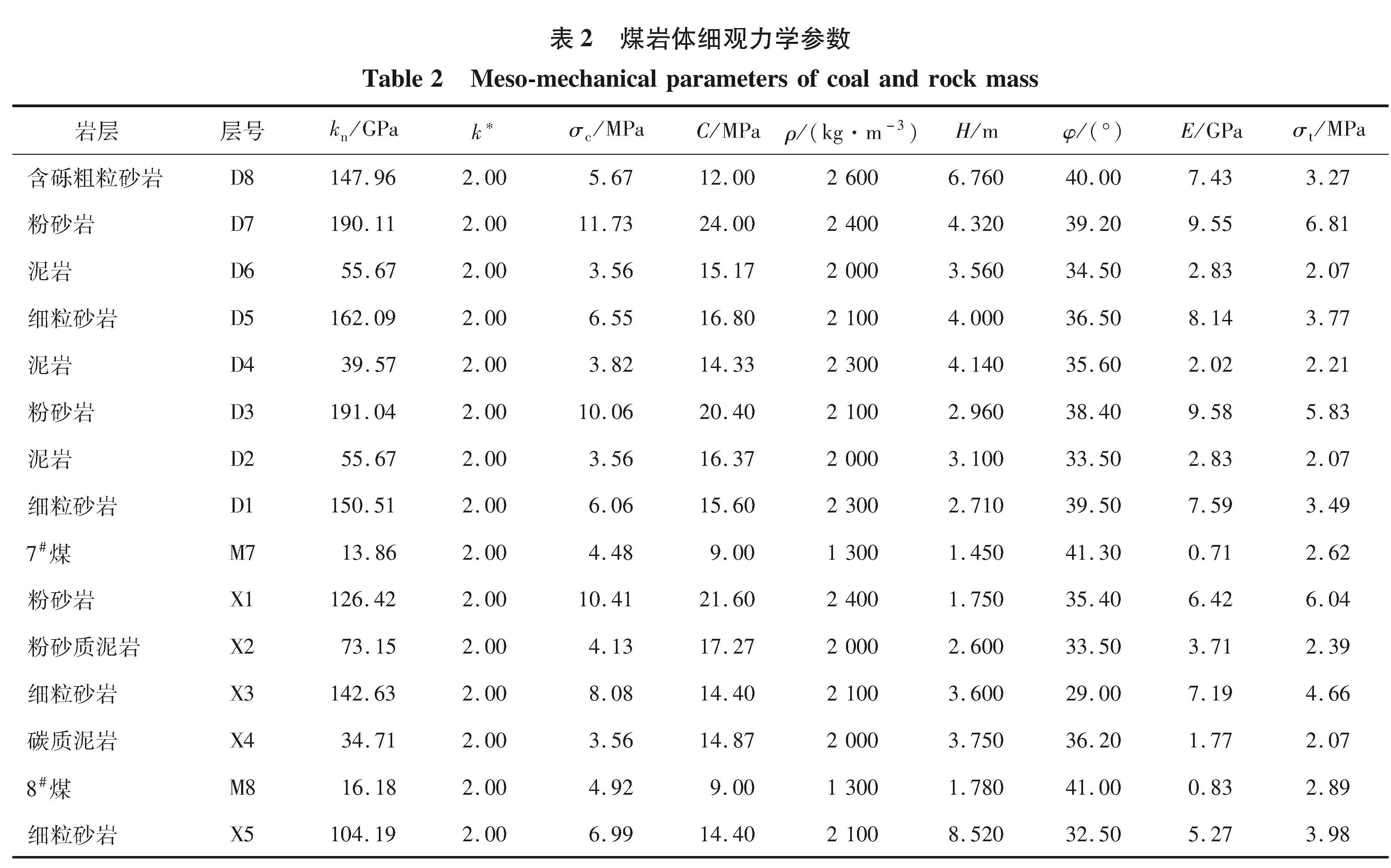
结合地质资料中岩层的力学及式(7),可计算出如表2所示的煤岩体细观参数及宏观参数模拟值。通过将细观参数代入单轴抗压-抗拉数值模型, 计算获得了细观参数预估值对应的弹性模量E及抗拉强度值σt。对比实际岩层及模型中的弹性模量及抗拉强度,两者标准差为0.085 7,误差范围较小,故模型采用通过式(7)获得的细观参数。
2.3 模拟结果
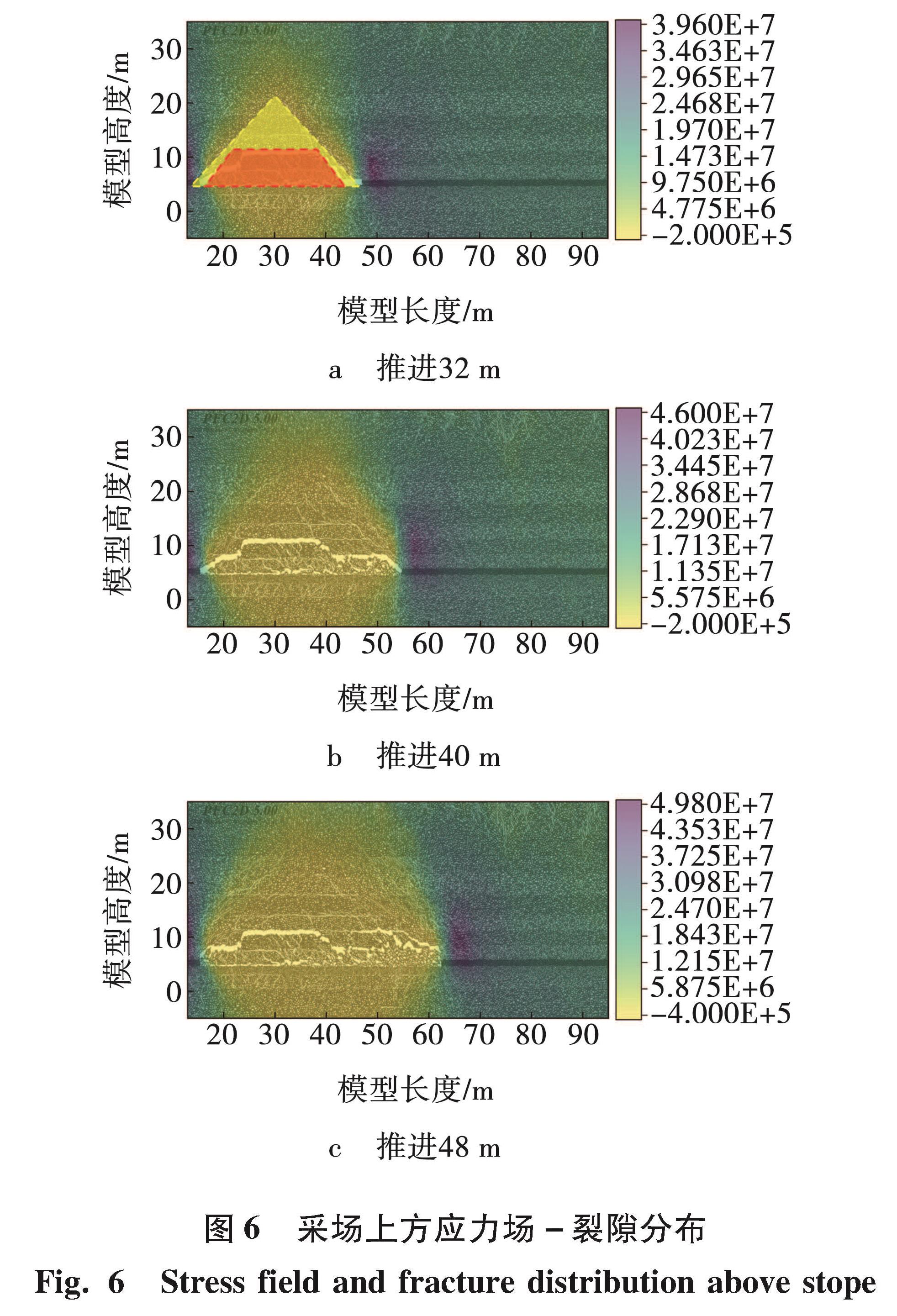
图6展示了不同推进距离下,顶板的裂隙发展、垮落形态及应力场。由图6可知,随着工作面的推进,顶板载荷沿应力拱向两侧煤柱转移,采空区上方出现逐渐扩大的等腰三角形状应力释放区。其中应力释放区边界岩层内的主应力方向倾角略小于边界走向倾角,且主应力大小随工作面推进而增加。如图6a所示,推进距离达到极限破断距后,岩层沿破断面发生破坏和垮落,从应力释放区和垮落区的分布情况可知,垮落块体破断面的倾角明显大于主应力方向倾角,与图1中的理论分布规律相符。
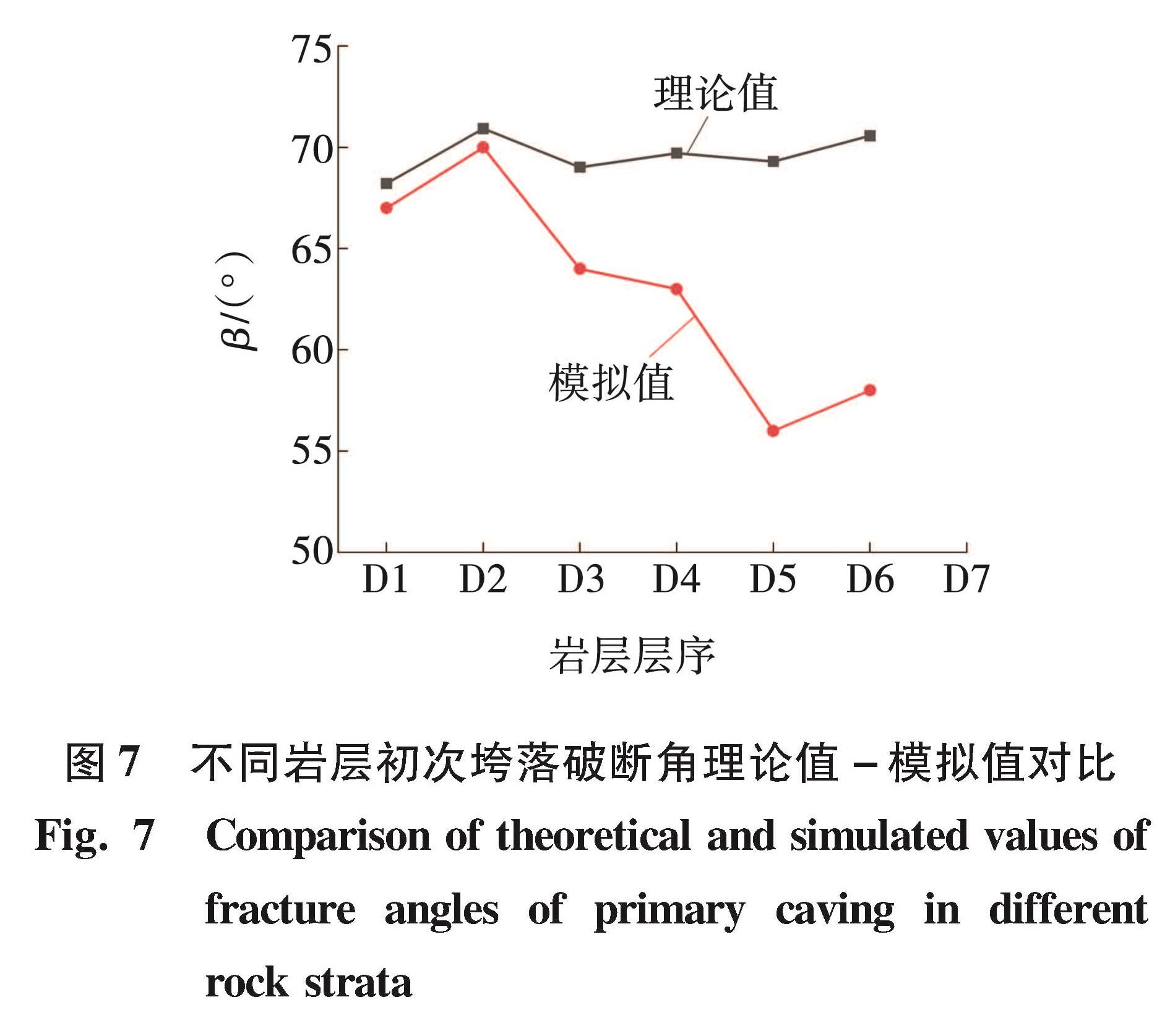
不同岩层初次垮落时破断角理论值和模拟值的对比曲线如图7所示。由图7可知,D1、D2岩层初次垮落时的破断角模拟值与理论值相近,而D3~D6岩层的破断角模拟值远小于理论值。结合图6中的顶板的垮落形态可知,D1、D2岩层周期破断时产生的碎块重新充填了较薄的采空区,并对上覆岩层起到了支撑作用,而岩层在逐渐增加的上覆载荷作用下继续发生破坏。故D3~D6初次破断垮落时的实际块体长度L远小于初次垮落时的理论块体长度LC/2。
图7 不同岩层初次垮落破断角理论值-模拟值对比
Fig.7 Comparison of theoretical and simulated values of fracture angles of primary caving in different rock strata
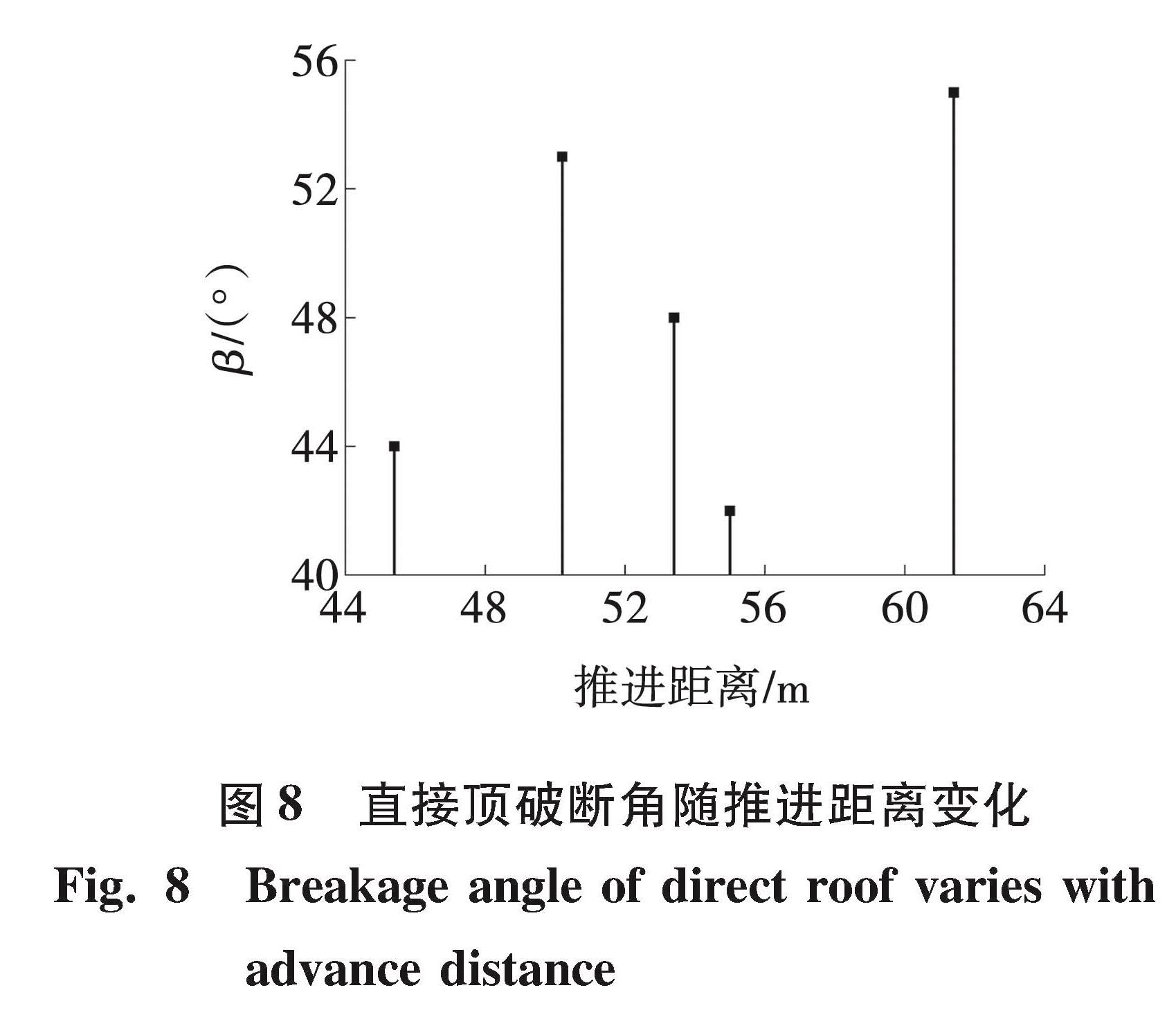
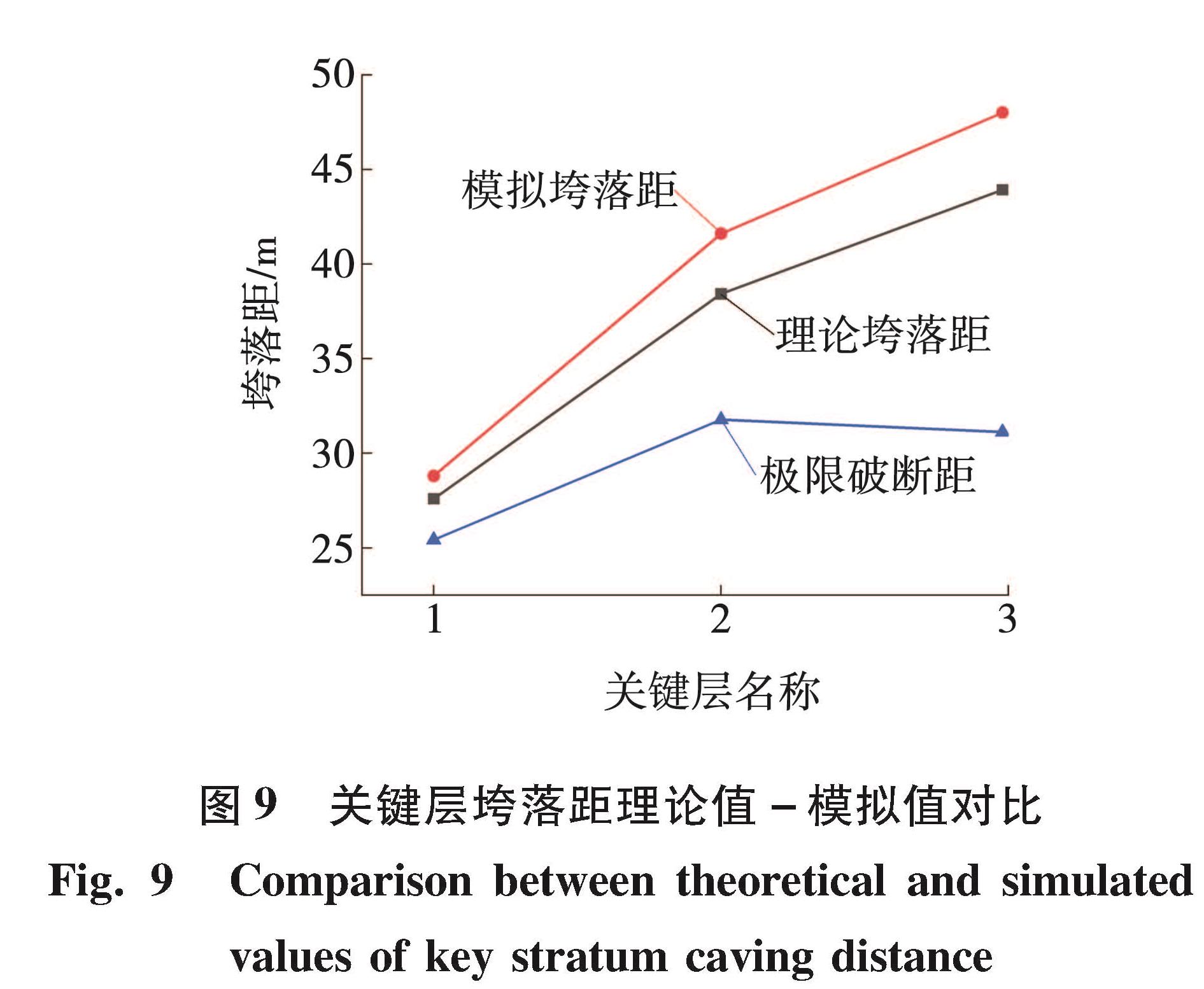
图8为直接顶初次垮落后,破断角随工作面推进距离的变化,图中的每一个数据点均代表直接顶的一次垮落。从图8可知,顶板的下次破断角随着垮落间隔的增加而扩大,随着垮落间隔的减小而降低,与破断角β的计算式(4)中破断角的大小与块体的长度成正相关相同。各关键层初次垮落时,垮落距理论值、模拟值及极限破断距如图9所示。
图9 关键层垮落距理论值-模拟值对比
Fig.9 Comparison between theoretical and simulated values of key stratum caving distance
由图9可知,垮落距的模拟值与理论值基本保持一致,验证了考虑破断角的顶板垮落距计算公式(6)。其中关键层2、3受垮落块体的影响,垮落距模拟值略大于理论值。同时垮落距的模拟值与理论值均明显大于极限破断距,故在顶板厚度较大、大采高及主关键层较远等破断面跨度大的工况中,需考虑破断角对垮落距的影响作用。
3 结 论(1)基于材料力学及岩体力学,分析了考虑破断角时顶板的垮落规律,并结合极限破断距理论,推导了考虑破断角的关键层初次垮落距计算公式,并通过数值模拟,对破断角及考虑破断角的关键层初次垮落距进行了验证。
(2)模型中D1、D2岩层的初次垮落时的破断角与理论值差值小于1.5°,直接顶D1岩层破断角的变化范围为42°~55°,且破断角大小与工作面推进时形成的块体长度存在与计算公式相符的正相关。
(3)模拟中各关键层的初次垮落距为28.8、41.6和48 m,除2、3关键层受垮落体的支承作用影响略大于理论值,各关键层初次垮落距的模拟值与理论值保持一致,且差值均远小于与极限破断距的差值,说明结合破断角的理论计算公式具有较高的可适用。
- [1] 许延春, 李俊成, 刘世奇, 等. 综放开采覆岩“两带”高度的计算公式及适用性分析[J]. 煤矿开采, 2011, 16: 4-7.
- [2] 许延春, 刘世奇, 柳昭星, 等. 近距离厚煤层组工作面覆岩破坏规律实测研究[J]. 采矿与安全工程学报, 2013, 30: 506-511.
- [3] 刘红威, 赵阳升, Ren T X, 等. 切顶成巷条件下采空区覆岩破坏与裂隙发育特征[J]. 中国矿业大学学报, 2022, 51: 77-89.
- [4] 武猛猛, 王 刚, 王 锐, 等. 浅埋采场上覆岩层孔隙率的时空分布特征[J]. 煤炭学报, 2017, 42: 112-121.
- [5] 谢生荣, 陈冬冬, 孙颜顶, 等. 基本顶弹性基础边界薄板模型分析(Ⅰ)——初次破断[J]. 煤炭学报, 2016, 41: 1360-1368.
- [6] 刘学生, 宁建国, 谭云亮. 近浅埋煤层顶板破断力学模型研究[J]. 采矿与安全工程学报, 2014, 31: 214-219.
- [7] 许 斌, 蒋金泉, 代 进, 等. 采场上覆关键层破断角的力学推导和实验模拟[J]. 煤炭学报, 2018, 43: 599-606.
- [8] 贺雁鹏, 黄庆享, 王碧清, 等. 浅埋煤层大采高工作面顶板破断角实测研究[J]. 采矿与安全工程学报, 2019, 36: 746-752.
- [9] 申 超. 近距离厚煤层开采的矿压显现规律研究[J]. 中国新技术新产品, 2020, 42(6): 118-119.
- [10] 叶俊良, 周志刚. 浅埋深特厚煤层综放开采地表异常塌陷原因分析[J]. 煤矿开采, 2018, 23: 77-80.
- [11] 吕志金. 大采高超长工作面矿压控制关键技术研究与实践[D]. 太原: 太原理工大学, 2017.
- [12] 刘 淑. 综采工作面老顶初次来压步距的理论预测[J]. 民营科技, 2013, 163(10): 75.
- [13] 钱鸣高, 石平五, 许家林. 矿山压力与岩层控制[M]. 徐州: 中国矿业大学出版社, 2010.
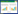 图 1 破断面应力分布
Fig.1 Stress distribution of broken section
图 1 破断面应力分布
Fig.1 Stress distribution of broken section